某型导弹动导数风洞试验和CFD数值模拟

岑梦希，张瑞民

(1.中国航天空气动力技术研究院 彩虹无人机科技有限公司，北京 100074) (2.中国航天空气动力技术研究院 第二研究所，北京 100074)

0 引 言

随着军事科技水平的不断进步，飞行器型号设计越来越复杂，尤其对于带翼的细长体飞行器，在高速、大攻角状态下，其阻尼导数对飞行器响应具有重要的影响[1-2]。对于型号工程设计来说，有效而精确的性能评估至关重要。为了能够确定新型导弹的气动性能，设计人员常借助于飞行测试，但复杂型号的飞行测试既耗时又昂贵；有些型号甚至出现极端的流场状况，即便是风洞试验也难以实现，无法满足未来型号研制的需求。

CFD技术不仅消除了飞行测试和风洞试验的条件限制，还大大降低了设计成本，且避免了测试中的危险[3]。目前为止，国内外关于飞行器动导数研究开展了大量的工作。Zhang Weiwei等[4]采用高效的当地活塞理论对超音速和高超音速下的无粘非定常压力载荷进行了预测；卢学成等[5]将气动力工程算法推广到非定常气动力计算中，求解任意外形飞行器作强迫振荡运动的非定常气动力，进而获得该飞行器的动导数；刘溢浪等[6]采用基于定常CFD技术的当地活塞理论提出了一种高效高精度的超音速、高超音速飞行器动导数的计算方法，并通过两个国际标模算例进行对比验证；Da Ronch A等[7-8]采用线性频域的谐波平衡法预测飞行器的周期性非定常流动特性，计算效率大大提高；David H等[9]采用时域谐波平衡法计算超音速导弹和民航飞机的俯仰动导数；陈琦等[10]采用谐波平衡法预测标模导弹的动导数，计算效率约为双时间推进法的13倍，且在大攻角动态特性计算中取得了令人满意的结果；张莽等[11]在高超声速激波风洞建立了瞬时动导数试验技术，并获得马赫数为8时10°尖锥模型的动导数，且精度较高。综合来看，尽管国内外学者在动导数计算方面做了大量的工作，但是关于亚音速导弹动导数方面的研究比较少，也很少将这些研究成果应用于工程型号研制。

本文应用缩比模型风洞试验方法和数值模拟方法分别对某型导弹的俯仰和滚转动导数进行研究，为工程型号研制提供支持。

1 风洞试验

1.1 试验方法

试验采用自由振动方法，该方法模拟飞行器飞行时受到扰动而产生角运动时的衰减过程。为保证风洞试验时模型角运动的减缩频率与真实飞行的减缩频率一致，需根据真实飞行器的转动惯量和静力矩确定真实飞行的自然频率，然后根据模型的缩比关系确定模型的减缩频率。

1.2 试验模型

本试验在FD06风洞进行。试验缩比模型安装如图1所示。导弹外形尺寸如图2所示，头部为圆形，弹身为圆柱形，弹身带4片弹翼，尾部带4片梯形舵，呈“X”字布局。

图1 风洞试验模型安装图

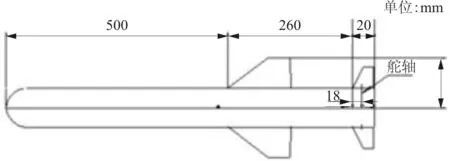
图2 导弹外形尺寸图

1.3 试验条件

风洞试验的基本条件参数如表1所示。测力及动导数试验采用高精度微型六分量杆式天平，天平静态测量精度小于0.2%，重复性试验均方根误差为1%。动导数测试方法采用频率10 Hz，振幅1°的单自由度俯仰或滚转运动。

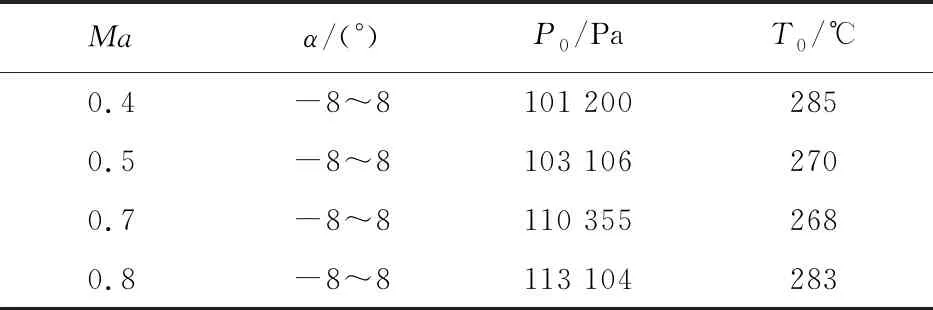
表1 试验条件

1.4 试验结果

1.4.1 状态曲线

马赫数为0.5，攻角为0°时的俯仰运动典型振幅衰减曲线如图3所示。马赫数为0.5，滚转角为0°时的滚转运动典型振幅衰减曲线如图4所示。

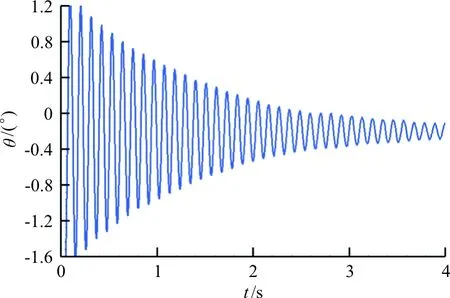
图3 典型俯仰运动振幅衰减曲线

图4 典型滚转运动振幅衰减曲线

1.4.2 试验数据

不同马赫数下俯仰动导数随攻角变化的曲线如图5所示。

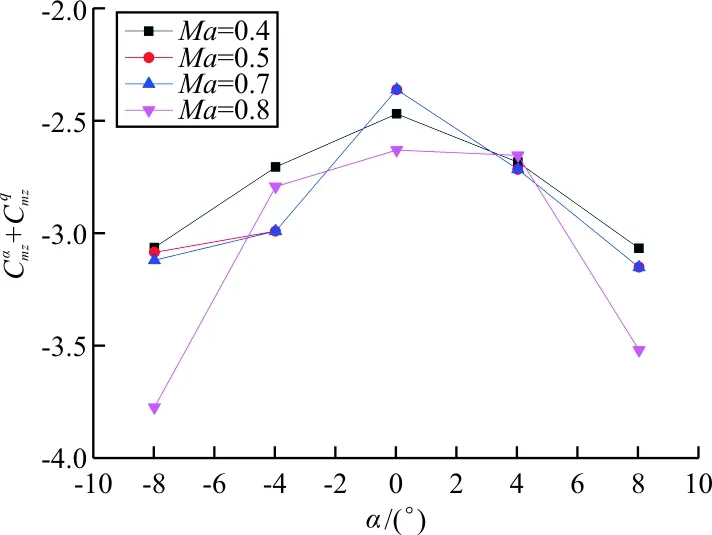
图5 不同马赫数下俯仰动导数随攻角变化

从图5可以看出：在不同马赫数下，动导数曲线沿纵轴α=0°接近对称；不同马赫数、不同攻角下的动导数均小于0，说明该型导弹在俯仰方向都是动态稳定的；俯仰动导数随着马赫数的增加，略有增大，但在跨音速马赫数0.8、某些攻角状态下，由于流场的振荡，俯仰阻尼的变化不符合此规律；俯仰动导数随着攻角绝对值的增加而增大，说明动稳定性随着攻角的增加而增强。

不同马赫数下滚转动导数随攻角变化的曲线如图6所示。

图6 不同马赫数下滚转动导数随攻角变化

从图6可以看出：在不同马赫数下，动导数曲线沿纵轴α=0°几乎完全对称；不同马赫数、不同攻角下的动导数均小于0，说明该型导弹是动稳定的；滚转动导数与马赫数的变化趋势一致，随着马赫数的增大，滚转阻尼导数缓慢增大，马赫数为0.4的滚转阻尼明显小于马赫数为0.5，0.7和0.8的滚转阻尼；所有马赫数下的滚转动导数随着攻角的增加而增大，说明动稳定性随着攻角的增加而增强。

2 数值计算

2.1 控制方程

流场计算采用有限体积法来求解时均N-S方程积分表达式如下：

(1)

式中：Q、Fc和Fv分别为守恒变量、对流通量和粘性通量，这些量的具体表达式可参考文献[2]。

湍流模型采用Transition SST模型。该模型是在SSTk-w的基础上增加了有关间歇度γ和转捩发生准则的两种输运方程，其捕捉流场细节精度更高。空间离散采用格心格式的有限体积法，时间离散采用隐式离散方法进行双时间推进。

2.2 动网格技术

动网格技术可以用来模拟流场边界随时间变化的问题。在任一控制单元中，广义标量Ф的积分守恒方程为

(2)

式中：ρ为流体密度；u为速度流量；ug为移动网格的网格速度；Γ为扩散系数；SΦ为源项；∂V为控制单元V的边界；A为控制单元的面积。

2.3 动导数积分法

以俯仰组合动导数为例，当刚体飞行器作低频小振幅的俯仰强迫振动时，其强迫振动模型的运动方程为

α=α0+αmsin(ωt)

(3)

式中：α0为初始攻角；αm为振荡幅值；ω为振荡圆频率。

气动俯仰力矩是状态变量及其对时间的各阶导数的函数，且计算中仅考虑一阶动导数，忽略高阶动导数可得

(4)

式(4)沿迟滞环线积分且无因次化，可得俯仰组合动导数为

(5)

式中：k=ωd/2v为减缩频率；d为翼体弦长。

2.4 计算与分析

模型网格划分如图7所示，其中，图7(a)为对称面网格及物面网格，图7(b)为轴向网格及物面网格，图7(c)为远场网格。总网格量约506万，壁面第一次网格高度为1×10-5m。

(a) 对称面网格及物面网格

(b) 轴向网格及物面网格

(c) 远场网格

2.4.1 俯仰动导数

马赫数分别为0.4和0.7时俯仰动导数随着攻角变化的曲线如图8所示。

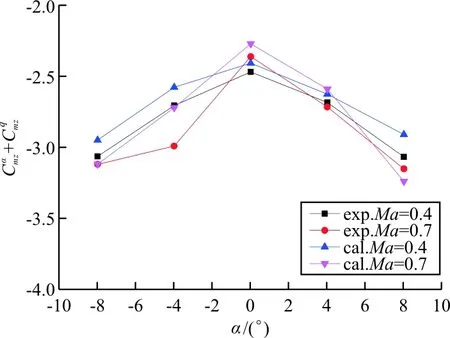
图8 俯仰力矩动稳定性导数随攻角的变化

从图8可以看出：当马赫数为0.4时，俯仰动导数计算结果与试验结合吻合较好，且变化曲线沿α=0°接近对称；当马赫数为0.7时，俯仰动导数计算结果与试验结果符合相对较好，但变化曲线沿α=0°时对称性较差，尤其在α=-4°时，试验结果数值偏大，这可能是由于接近跨音速时流场内的激波干扰和模型支撑干扰造成的。

2.4.2 滚转动导数

马赫数分别为0.4和0.7时模型滚转力矩动导数随着攻角变化的曲线如图9所示。

图9 Finner导弹的滚转力矩动稳定性导数

从图9可以看出：在不同马赫数下，滚转力矩动导数计算结果与试验结果吻合较好，且变化曲线关于α=0°接近对称。

3 结 论

(1) 本文采用自由振动方法进行的缩比模型风洞试验与强迫振动数值模拟方法获得的结果吻合良好，可为型号设计服务。

(2) 从风洞试验和强迫振动数值模拟方法获得的结果可以看出，在不同马赫数、不同攻角下，某型导弹在俯仰和滚转方向上都是动态稳定的；在不同马赫数下，俯仰和滚转方向上的动导数曲线沿纵轴α=0°接近对称；在不同马赫数下，俯仰和滚转方向上的动稳定性随着攻角绝对值的增加而增强。

(3) 本文CFD数值模拟方法计算精度较高，且是风洞试验的有力补充，不仅可以用于型号设计验证，而且可以拓展更大参数范围内的动导数研究工作。