桨叶实度及轴间距对摆线桨气动特性影响研究

冯旭碧，朱清华，雷良，黄杰

(南京航空航天大学 直升机旋翼动力学国家级重点实验室，南京 210016)

0 引 言

摆线桨是一种新型的全向矢量推力装置，由于具有操纵性能好、气动效率高和噪音低的优点，将其作为未来垂直起降飞行器、高空长航时无人机、飞艇和舰船等诸多领域的推进/升力系统具有较好的应用前景[1-3]。而设计参数的选择和气动性能是影响摆线桨应用前景的关键因素，虽然国内外已经对摆线桨开展了相关研究，但关于气动参数特性研究的文献并不多，甚至由于试验或测量误差的原因，不同文献中得出不同的结论。例如文献[4]和[5]均通过试验研究了半径的影响，但前者指出相同弦长时气动力随半径的变化不大，而后者表明半径越大气动力越大。同时，文献[6]以功率载荷为参照，对翼型厚度、俯仰轴位置及最大俯仰角等部分设计参数进行了分析，而对半径和弦长等参数未进行研究，并且没有研究参数影响的耦合作用。

本文首先研究与实度相关的设计参数，将半径、弦长和桨叶数归纳为实度的影响，总结实度与单位面积上桨叶载荷的关系，然后分析摆线桨相互之间的气动干扰特性，国内外学者还未对这方面进行过研究。

1 建模计算

1.1 摆线桨原理

摆线桨主要由支架、偏心控制机构及两片以上的桨叶等构成，其三维原理图如图1所示，桨叶展向与旋转轴平行，桨叶在绕转轴公转的同时，桨叶绕变距轴做俯仰振荡[1]。桨叶桨距角随方位角的变化，桨叶在底部和顶部时都产生正升力如图2所示，可以通过改变桨距角幅值或转速控制力的大小，改变偏心装置的相位角控制力的方向。

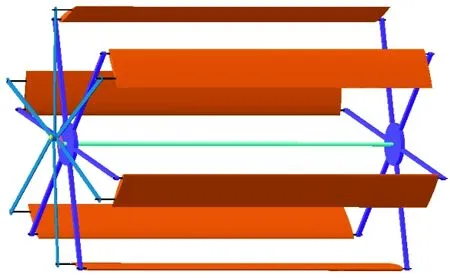
图1 摆线桨原理图

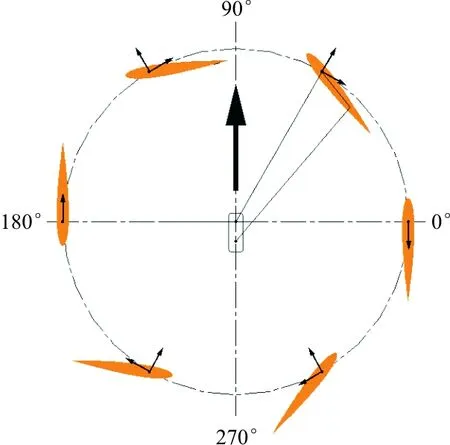
图2 桨距角随方位角的变化

1.2 模型建立与网格划分

采用Fluent的非定常数值模拟模块，分析摆线桨的气动机理和桨叶间干扰。因为摆线桨桨叶为直桨叶，桨叶展向的形状和运动规律几乎一致，所以展向流场变化较小，考虑到计算量和计算时间的效益，将摆线桨简化为二维网格进行数值模拟。

摆线桨二维网格示意图如图3所示，采用滑移网格技术[7-8]，将计算域划分为：外部静止域、旋转域和包含桨叶的旋转区域，为了更好捕捉桨叶附近的流场细节，在桨叶周围添加边界层网格。本文采用适合于求解低速不可压缩流动的压力基求解器，文献[10]表明采用S-A模型和SST均可较好的计算摆线桨的升力，但前者对功率的计算更准确，因此本文选取S-A模型。桨叶桨距角的变化规律以正弦函数近似描述，通过用户自定义函数(UDF)中的DEFINE_ZONE_MOTION宏实现。

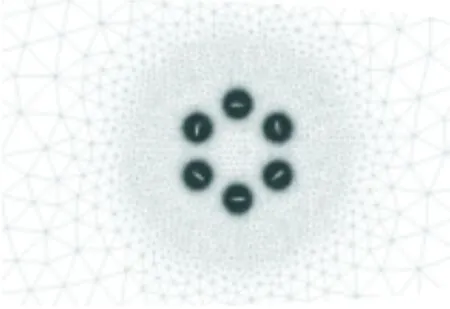
(a) 全局网络

(a) 局部网络

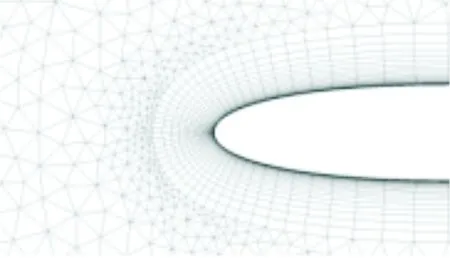
(a) 附面层网络

1.3 网格无关性验证

对于非稳态数值模拟，需要确定所用网格数与结果之间的无关联性，即网格无关性验证，本文主要探讨计算结果中竖直拉力的无关性检验。对A，B，C三种网格数量进行无关性检验，得出的结果如表1所示。

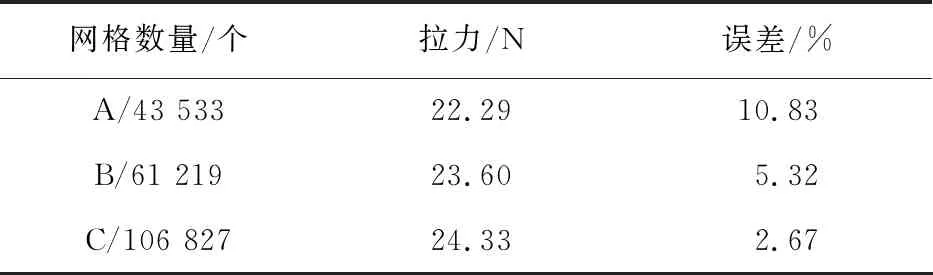
表1 网格无关性验证结果

从表1可以看出：网格数量对模拟结果具有极大影响，网格数量低于4.3万时，计算结果与试验值有较大误差，而当网格数数量超过6万时，模拟结果变化差异不大。

1.4 数值模拟方法验证

为了检验本文CFD数值模拟方法的有效性，以韩国首尔大学的摆线桨静拉力试验为算例[6]，该试验中摆线桨的设计参数为：半径R为0.4 m，弦长c为0.15 m，展长b为0.8 m，最大俯仰角为25°，采用NACA0012翼型。通过CFD计算所得摆线桨的速度云图和速度流线图分别如图4和图5所示，CFD拉力计算值与试验值的对比曲线如图6所示。

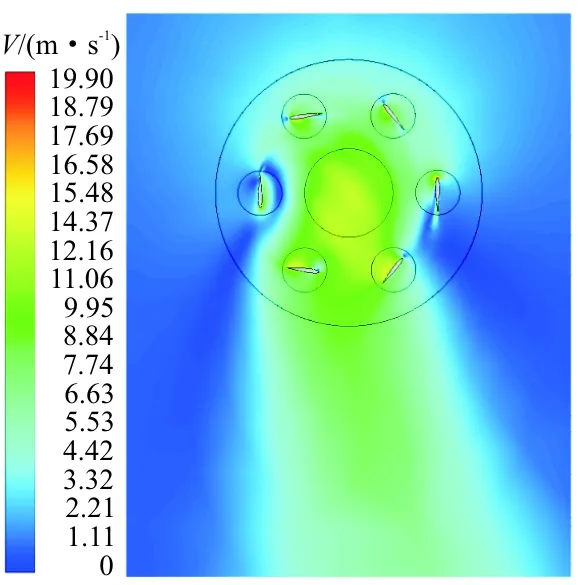
图4 摆线桨速度云图

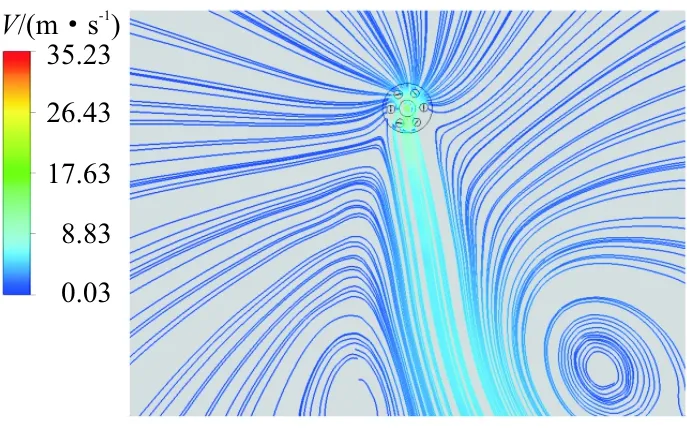
图5 摆线桨流线图

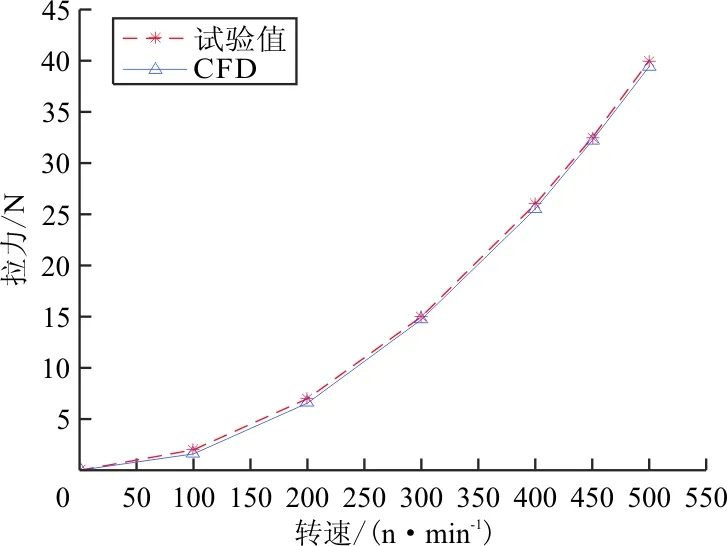
图6 拉力计算值与实验值对比(Nb=6)

从图6可以看出：二维数值模拟结果与试验值吻合较好。因此，采用二维非定常数值模拟方法研究摆线桨的气动特性和参数影响是可行的。

2 气动参数特性研究

为了更清楚观察实度对气动性能的影响规律，相关的设计参数主要包括半径、弦长和桨叶数。摆线桨气动力系数以无量纲形式表示为[11]：

(1)

摆线桨实度表示为：

(2)

式中：T为摆线桨产生的气动力；Ω为角速度；b为摆线桨展长；d为直径；R为半径；Nb为桨叶片数；c为桨叶弦长。

2.1 半径影响

摆线桨不同半径时竖直拉力随转速的变化如图7所示。

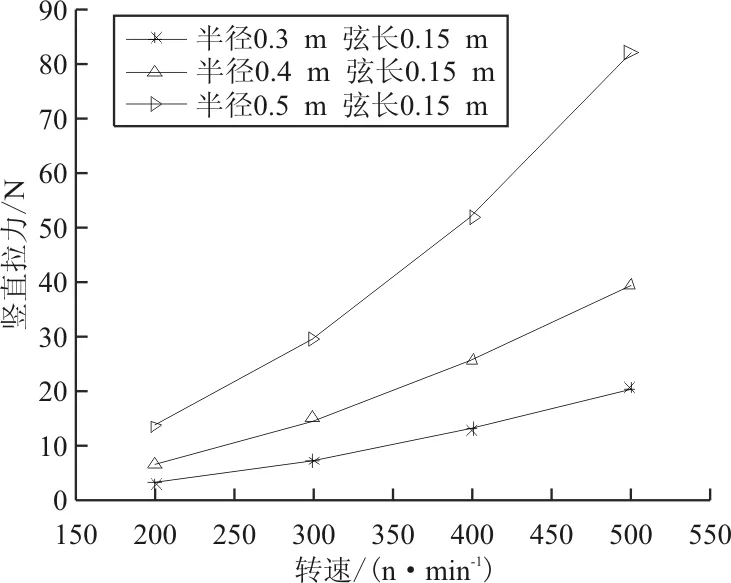
图7 不同半径下拉力随转速变化曲线(Nb=6)

从图7可以看出：半径越大，竖直拉力越大，且半径越大，竖直拉力增加越明显。桨叶单位面积上载荷(CT/σ)随转速的变化如图8所示。

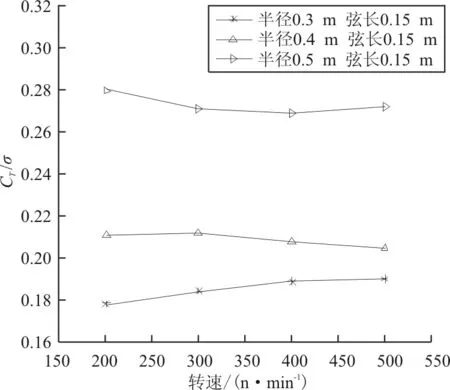
图8 不同半径下CT/σ随转速变化曲线(Nb=6)

从图8可以看出：与拉力变化一致，半径越大，桨叶单位面积上载荷越大。

2.2 弦长影响

选取半径为0.5 m，弦长分别为0.10 m，0.15 m和0.20 m的摆线桨为研究对象，研究桨叶间的干扰特性如图9～图10所示。从图9和10中对比看出：虽然摆线桨产生的拉力随弦长的增加而增加，但是桨叶单位面积上的载荷反而减小。且由于弦长越大，桨叶间干扰增加，竖直拉力增加效果越不明显。

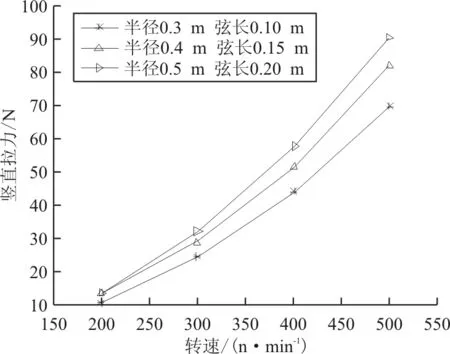
图9 不同弦长下拉力随转速变化曲线(Nb=6)

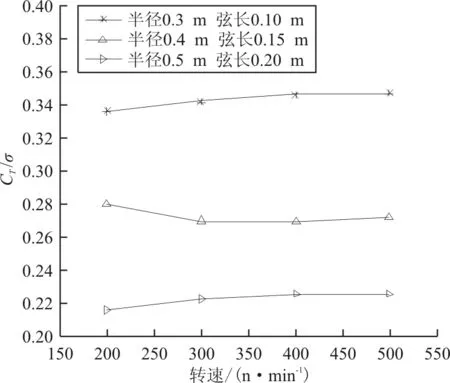
图10 不同弦长下CT/σ随转速变化曲线(Nb=6)

2.3 桨叶数影响

相同半径和弦长时，桨叶片数对摆线桨气动性能的影响如图11～图12所示。

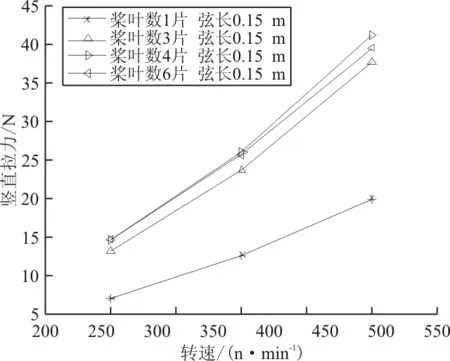
图11 不同桨叶数下拉力随转速变化曲线

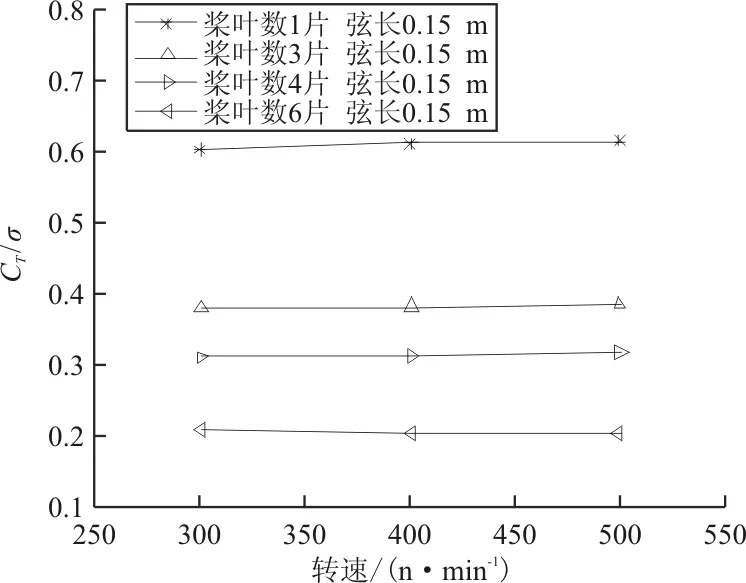
图12 不同桨叶数下CT/σ随转速变化曲线

从图11～图12可以看出：相同条件下，4叶片产生的拉力最大，且在较高转速时，拉力明显高于6叶片，而图12表明单叶片的桨叶载荷最高，3叶片、4叶片和6叶片依次减小，这可能是由于桨叶数增加，桨叶间干扰增强造成的。桨叶载荷的对比如表2所示。

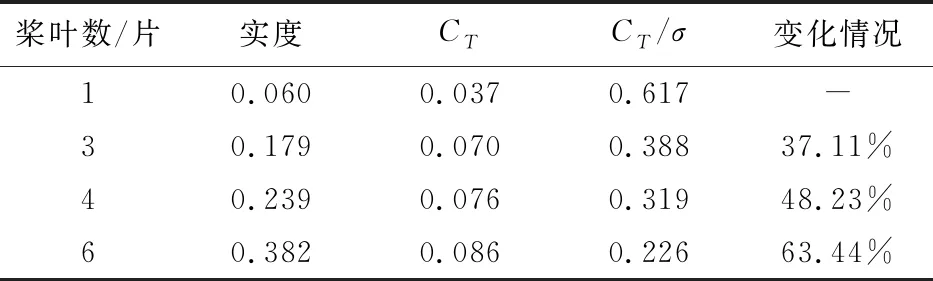
表2 桨叶数对桨叶载荷的影响

桨叶数对周期气动力的影响如图13～图14所示，可以发现桨叶数对摆线桨的气动力影响较大[12]，主要影响区域是方位角30°～150°和240°～300°。

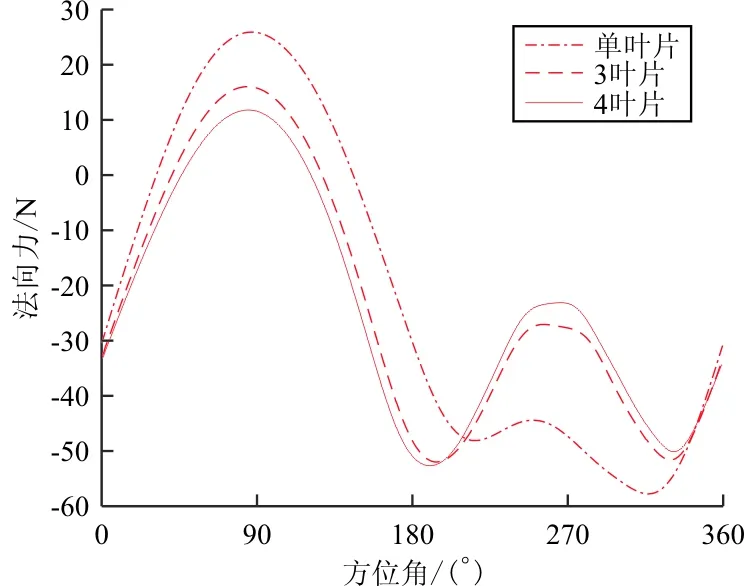
图13 不同桨叶数法向力对比

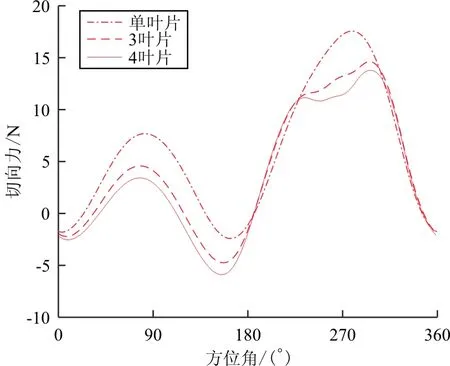
图14 不同桨叶数切向力对比

摆线桨产生的合力随实度和转速变化的关系如表3所示。

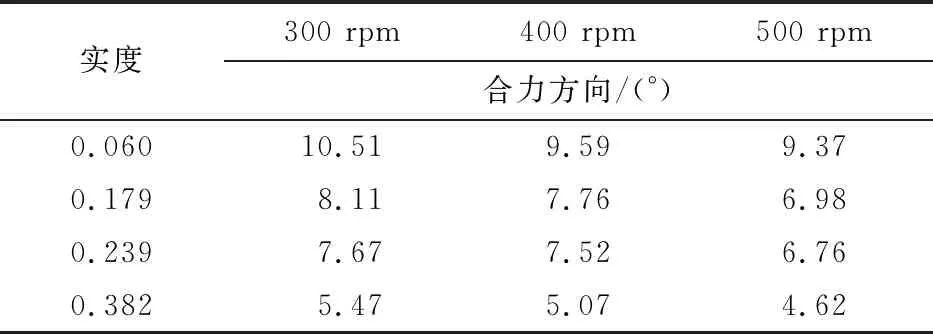
表3 合力方向随实度及转速变化对比

从表3可以看出：摆线桨的转速和实度都会影响合力的方向。对单个摆线桨而言，转速和实度越大，合力与竖直方向的夹角越小。

3 双摆线桨气动特性研究

上一节中研究了单个摆线桨的气动参数特性，本节将应用同样的模型和方法分析不同间隔距离时，两个摆线桨之间的气动干扰特性，可以作为摆线桨总体布局的依据，研究模型如图15所示。

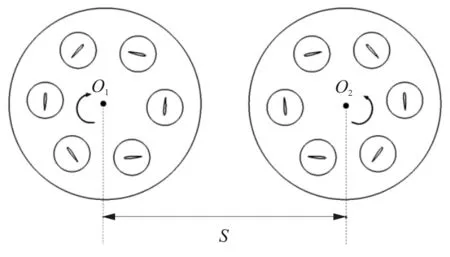
图15 两个摆线桨之间的纵向间隔距离S

当两摆线桨间距分别为4R，5R和6R，转速为600 rpm时，摆线桨的升力损失系数及合力方向的变化如表4所示，可以看出：随摆线桨间距离的增大，合力偏转角减小。不同间距时，摆线桨速度云图和速度流线图的对比分别如图16～图17所示。

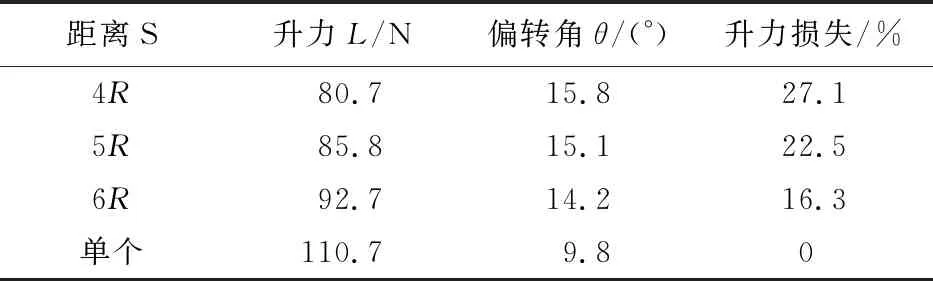
表4 不同纵向间隔的升力与偏转角比较

(a) 纵向间隔4R

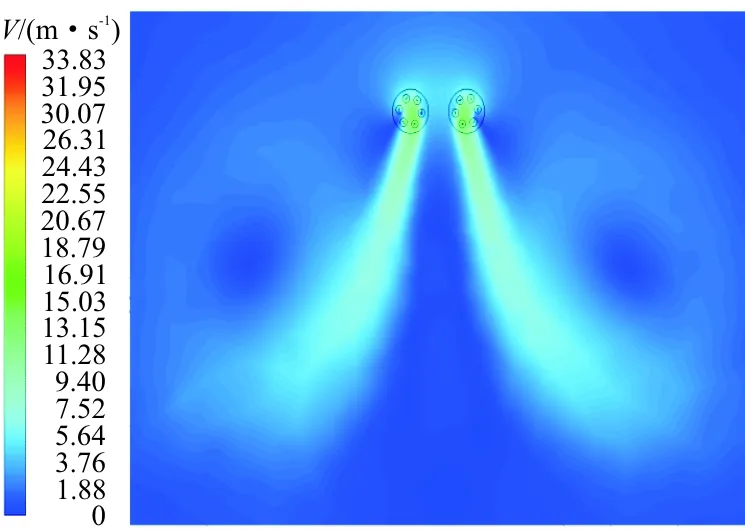
(b) 纵向间隔5R

(c) 纵向间隔6R

(a) 纵向间隔4R

(b) 纵向间隔5R

(c) 纵向间隔6R

4 结 论

(1) 摆线桨半径越大，气动力越大，随转速的增加更明显，桨叶载荷越大，桨叶间干扰越小。

(2) 虽然摆线桨产生的推力随弦长的增加而增加，但是桨叶单位面积上的载荷反而减小。因此，弦长越大，桨叶间干扰越大，推力增加效果越不显著。

(3) 相同条件下，4叶片摆线桨产生的气动力比3叶片和6叶片大，而3叶片的桨叶载荷最大。

(4) 摆线桨合力的方向与转速和实度相关，合力偏转角分别随转速和实度的增大而减小。

(5) 随着摆线桨间距离的增加，气动力损失系数和合力偏转角均减小。

因此，在摆线桨设计中，需要综合考虑摆线桨关键设计参数和摆线桨间距离对气动性能的影响，从任务载荷需求、气动高效性、结构紧凑性等多方面进行考虑，进行摆线桨的参数选择和总体布局。