生长：让学生的数学学习活力无限

李艳红

【摘要】数学，是研究数量关系和空间形式的科学。数学学科的知识体系，应该是一个完整的、系统的结构。但在实际教学中，教材不得不把整体的知识结构分割成一个个学段、一个个学期、一个个章节、一个个课时来实施教学。虽然是分散了教学，但是整个数学教学应呈现“生长”之态，教学内容前延后伸、习题设计左接右连、解题方法明喻暗引、数学思想上启下承。

【关键词】数学教学;生长;融合;联结;贯通;扩展

數学，是研究数量关系和空间形式的科学。数学学科的知识体系，应该是一个完整的、系统的结构。但在实际教学中，教材不得不把整体的知识结构分割成一个个学段、一个个学期、一个个章节、一个个课时来实施教学。从表面看，教师是在一点一点地教，学生也是在一点一点地学。在学习的过程中，学生陆续习得许许多多的点状知识。然而这许许多多的点状知识，虽以点状习得，又应归于知识整体。为此，数学教学的过程要努力呈现知识的生长态，让学生看到一粒沙中的世界、一滴水中的大海、一棵树后的森林。

一、内容层面追求前延后伸：“归一根，成一体”

教学用书上每一单元的教材说明和教学建议，总是以“已学过的相关内容→本单元的主要内容 →后续学习的相关内容”来显示本单元的教学内容及前后联系。每一单元是如此，每一新授也是如此。多数新课的展开，总是从复习开始。课前复习可以复习刚学过的知识，对知识加以巩固;更多的是复习与新知有关联的旧知，将内容上的前延后伸联系起来，帮助学生更好地建构知识体系。

例如苏教版一年级下册第四单元《100以内的加法和减法（一）》中，教材先安排教学口算两位数加整十数、一位数，熟练方法后再教学口算两位数减整十数、一位数。教学口算两位数加整十数、一位数，引导学生体会的算法：几个十，加在十位上，先算几十加几十;几个一，加在个位上，先算几加几。口算两位数减整十数、一位数，其算理实质是一样的，只不过加减不同。这样一来，口算两位数减整十数、一位数其实就是对口算两位数加整十数、一位数算法的迁移，本是同根生、融合成一体。

教学口算两位数减整十数、一位数时，我这样引入——

出示：45+30，45+3，55+3，55+30。

（1）口算结果，并说一说口算的过程。

（2）说一说如何用小棒摆一摆或在计数器上拨一拨。

（3）“+”变“-”成45-30，45-3，55-3，55-30。现在该怎么计算呢？

小结时，我组织学生比一比，口算两位数加整十数、一位数的计算方法与口算两位数减整十数、一位数的计算方法有什么相同和不同的地方？从而将两者的计算方法进行融合，明确几个十，算在十位上;几个一，算在个位上，然后再将几个十和几个一合起来。

这样引入是计算方法的一种正迁移，将学生已有的知识经验积极地作用于新知识，促进新知识的系统化。而小结时的比较则更有必要，将计算方法进行融合，使口算两位数加减整十数、一位数的计算方法自成一个整体、一个体系，帮助学生达成学习内容上的前延后伸，使之“归一根，成一体”。

二、习题层面追求左连右接：“串一链，成一组”

每一新授知识总会伴随一系列的练习，这些习题，侧重有所不同，但都是为了巩固新知识服务的。相互之间虽以独立形态存在，却又不乏关联。将这种联系左右连接，将这些习题组成一个个知识块，以题链、题组的形式出现，让习题在顺延中生长。

例如《四边形、五边形、六边形的初步认识》是苏教版二年级上册第二单元第1课时的教学内容，直观认识四边形、五边形和六边形。想想做做中安排了5题有层次的练习活动，判断是不是四边形、按要求围出图形、分类整理多边形，以及一些操作性、开放性、综合性较强的练习（想想做做第4第5题如图1），让学生丰富对四边形、五边形和六边形基本特征的感知，发展初步的空间观念和实践能力。

尽管，按照课本的顺序一题接一题也可以完成本课时的练习。但是将有联系的内容“组成团”，将能用的题材“再利用”，练习更显流畅、更显生长性。实际教学时，我是这样设计想想做做第4第5题的，结合练习三的第1题安排了“折一折”“分一分”“数一数”三项活动——

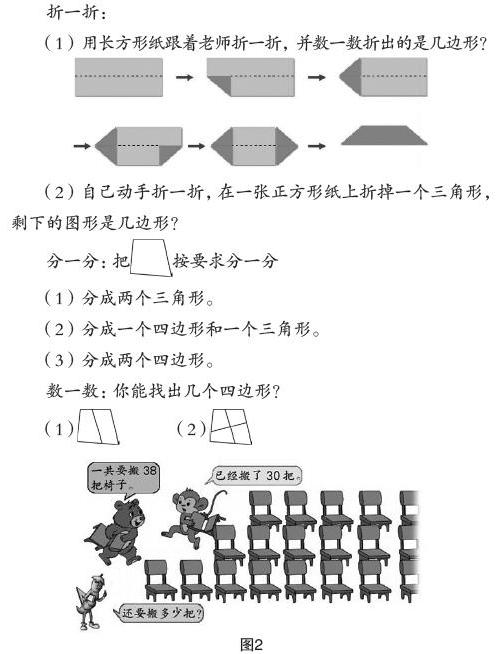
折一折：

（1）用长方形纸跟着老师折一折，并数一数折出的是几边形？

（2）自己动手折一折，在一张正方形纸上折掉一个三角形，剩下的图形是几边形？

分一分：把按要求分一分

（1）分成两个三角形。

（2）分成一个四边形和一个三角形。

（3）分成两个四边形。

数一数：你能找出几个四边形？

剪掉一个三角形变成折掉一个三角形，这样变一种选择成三种尝试。既然安排了折一折环节，我索性就让孩子玩得尽兴，将长方形纸也折一折，所以就设计了“用长方形纸跟着老师折一折”和“自己动手在正方形纸上折一折”。我将第4题的第（1）题设计成分一分，加上“分成两个四边形”的要求则为了能够“生长”出第5题，也给学生思维一个渐进的坡度。这样一来，结合问题之间的关联，左接右连，让学生左右逢源，从一个问题到一组问题的设计，让习题“串一链，成一组”。

三、方法层面追求明喻暗引：“学一法，通一片”

举一反三、触类旁通是课堂教学努力培养的学习能力，题无止境，但学之有道。从一个问题中提炼的解题方法，明喻暗引，再生长一番，促其贯通一类，即“学一法，通一片”。

例如学生完成苏教版一年级下册《整十数加一位数及相应的减法》想想做做7（如图2）后，教师追问：38-30=8（把）表示一共要搬38把椅子，已经搬了30把，还要搬8把。还可以表示什么实际问题？

又如原苏教版四年级下册的《解决问题的策略》例2用线段图（如图3）解决了行程问题后，擦去线段图上的条件（如图4）。教师指着线段图追问：你还能想到那些实际问题？这时，学生思维打开，看着线段图编实际问题，有的学生想到了“开凿山洞的实际问题”，有的学生想到了“打一份文件的实际问题”，有的学生想到了“购买商品的实际问题”……学生们跳出行程问题，走向工程问题，走向购物问题……不知不觉中就沟通了这一类题目的联系。

再如学生学习了苏教版三年级上册“长方形和正方形的周长”后，拓展部分不妨安排这样一个环节：“寻找差不多”——

师：要想求出下面图形的周长可以怎么算？要量几条边？为什么？

师：这些图形中，哪些和正方形的周长计算差不多？哪些和长方形的计算差不多？为什么？

这样的安排让学生不仅学会了求长方形和正方形的周长，还学会了用同样的方法求类似图形的周长。数学的解题方法是在对解决相关数学问题的举一反三、触类旁通中，通过对原有知识经验的迁移，形成结构化，使学生的数学思维走向深刻。平常教学中，教师可引导学生在比较中融会贯通，从而“学一法，通一片”。

四、思想层面追求上承下启：“发一点，长一树”

列举是解决问题的一种常用策略，亦是一种应用很广泛的策略。一年级的部分数学问题，也可以用列举的策略来解决。只是，一年级的孩子，还不能理解“列举”，于是我们称这种方法叫“先写出来”。

例如学生学习了苏教版一年级下册《认识100以内的数》后，就会出现这样的练习：“用3颗珠可以拨出（  ）个两位数，最小是（  ），最大是（  ）。”这个题目，答案远远没有得出答案的过程来得重要，尽管可以概括出“最大，将3颗珠子都拨在十位上;最小，十位拨一颗，其余拨在个位上”的方法，但对于大多数孩子而言，先让学生在计数器上拨一拨，然后有顺序地把可以拨出的两位数写出来，再去找出最大和最小的是最合适的方法。

又如学生学习了苏教版一年级下册《认识人民币》之后，教师补充练习“用1元、2元和5元的人民幣各一张，最多可以组成多少种不同的钱币？”，也是需要用列举的方法，先写出来再数一数。尽管小学生只是刚跨进数学大门的孩子，可是，数学思想和数学如影随形，有数学的地方，便不会找不到数学思想。

不光是列举，还有很多的数学思想方法都是从萌芽开始发展起来的，总是从模糊慢慢走向清晰，从笼统慢慢走向精确，从一个“大概”发展到“完整”，“发一点，长一树”。

画图也是解决问题的一种常见策略，示意图、线段图可以有效地帮助学生解决问题。这种策略不是高年级的专属，它亦是从萌芽开始发展起来的。

例如一年级学生常会面对这样的问题：“一些小朋友排成一队，小明前面有5人，后面有4人，这一队一共有多少人？”怎么解决呢，当然是先画一画，○○○○○●○○○○，瞧，白色圆圈表示小朋友，黑色圆圈表示小明自己，数一数，加一加，问题就解决了。将数字变大一点：“一些小朋友排成一队，小明前面有15人，后面有14人，这一队一共有多少人？”，数学思想方法一下子就“催生”出来了。怎样表示可以做到言简意赅？结果学生想出了如此图文并茂的“懒招”：15 ● 14，然后加一加，问题也解决了。

任何事物从无到有，都是从雏形开始发展起来的，数学思想方法也不例外。数学的生长性，亦是指扩展性，尤其是数学思想的上启下承，“发一点，长一树”。

生长，是数学教学的应然之态，让学生的数学学习活力无限。生长即融合，教学内容上的前后延伸，“归一根，成一体”;生长即联结，习题设计上的左接右连，“串一链，成一组”;生长即贯通，解题方法上的明喻暗引，“学一法，通一片”;生长即扩展，数学思想上的上启下承，“发一点，长一树”。教师努力站在系统化、整体化的角度审视课堂教学，努力帮助学生建构系统化、整体化的数学知识。

【参考文献】

[1]庄慧芬. 站起来的儿童数学[M].南京：江苏凤凰教育出版社，2015.

[2]陈芬芬. 关注图形特征  积累思维经验 [J] .教学月刊，2016（9）.