从高中物理核心素养视角盘点“力的分解”教学
陆峙秋 周新雅 周行 曾凡焱


摘 要:着眼于物理学科核心素养的视角,针对“力的分解”分别从2010年人教版教材与课标的修订、传统教学过程的反观、教学目标的解读以及利用几何画板有效辅助教学四个方面进行探讨,以求达到更加全面、准确的认识,更好地把握物理观念的科学建立。
关键词:核心素养;物理观念;力的分解
中图分类号:G633.7 文献标识码:A 文章编号:1003-6148(2019)5-0015-4
着眼于物理学科可知,在以前的某些知識的教学过程中,更多的是让学生学习一个个零散的知识点,且更注重这些知识点采用什么形式来考查,能够衍生出哪几种题型。这样的教学常常导致知识在学生头脑中是零碎的,而非一脉相承、触类旁通的。基于提升核心素养的视角,在物理教学过程中,一线教师应该从整个学科知识体系的宏观方面来认识各个知识点所拥有的功能,以及它在整个知识脉络中的地位,弄清它的本质内容,掌握它的教学要求。这样才能有效地将核心素养不断融入到教学中去,帮助学生从更高的角度认识知识的全貌,构建知识体系。
下面以“力的分解”教学过程为例,浅谈在核心素养视角下如何认识这一节内容。
1 课程标准和人教版教材修订后突出的改变
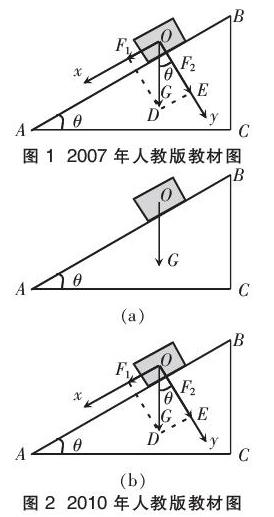
2007年人教版教材的内容片段[1]:“【例1】 把一个物体放在倾角为θ的斜面上。物体受到竖直向下的重力,但它并不能竖直下落。从力的作用效果看,应该怎样将重力分解?两个分力的大小与斜面的倾角有什么关系?分析:物体要沿着斜面下滑,同时会使斜面受到压力。这时重力产生两个效果,使物体沿斜面下滑,并使物体紧压斜面。因此重力G应该分解为这样两个分力,平行于斜面,使物体下滑的分力F1,垂直于斜面使物体紧压斜面的分力 F2 ,力的分解图如图1所示。”
物体所受重力使它下滑,同时紧压斜面,要根据这两个效果把力进行分解。
修订后2010年人教版教材的内容片段[2]:“【例2】 把一个物体放在倾角为θ的斜面上。物体受到重力,大小为G,方向竖直向下,如图2(a)所示(物体还受到其他力的作用,图中没有画出)。现在需要沿平行于斜面的方向和垂直于斜面的方向对物体的运动分别进行研究,为此建立直角坐标系如图2(b)所示。现在把重力G 沿两个坐标轴的方向分解为F1和F2,求两个分力的大小。”
按照图中给定的坐标轴,把重力G分解为F1和F2。
在2007年人教版的教材中是“根据力的作用效果”来进行力的分解,但在修订后的2010年人教版的教材中,则删除了“根据力的作用效果”来进行力的分解,而是强调“根据研究的需要”进行力的分解;教材作出的这一修改,需要教师从“运动与相互作用观”这一宏观角度重新审视“力的分解”这一节知识在物理观念中的地位,重新认识它的功能。
在普通高中物理课程标准中,对这一节的内容要求也发生了相应的改变。2003年版《普通高中物理课程标准》中对这一节知识的内容要求是“通过实验理解力的合成与分解,知道共点力的平衡条件,能区分矢量与标量。能用力的合成与分解分析日常生活中的问题。”在2007年版《普通高中物理课程标准》中则进行了修改,把“能用力的合成与分解分析日常生活中的问题”改为“能用共点力的平衡条件分析生产生活中的问题”,明显突出了“运动与相互作用的关系”,强调了共点力的平衡才是解决一系列实际受力平衡问题的核心知识,而“力的分解”则更强调它在解决这一问题过程中的工具性作用。
2 基于核心素养视角下的教学目标解读
教学“力的分解”究竟应达到怎样的教学目标是一个无法回避的问题,由上述修改后的教材例题和课标的改动可知,其目标是“学生是否会用力的分解求两个分力,分力的方向已知,那么分力的大小如何来确定?”而非“根据力的作用效果来求解分力”。“力的分解”是根据解决问题的需要,根据需要可把力分解在任意两个方向上,其目的就是“为了解决某个问题”。
在教学目标的设计上不要求学生把力的分解直接用来求解物体的受力情况,而是通过力的分解让学生学会“等效替换”的思想;让学生会用平行四边形(或三角形)定则求解有确定解的两个分力。
2010年人教版教材中,其例题和课后练习中都没有再提及“用力的分解来求解物体的受力”。例题中是已知两个分力的方向求两个分力的大小;在课后练习中的另一种题型是已知一个分力的大小和方向,求解另一个分力的大小和方向。其难点在于矢量三角形与实物三角形的几何关系、边角关系。
反思这样的安排可知,教材就是要摆正“力的分解”在整个“力与相互作用观”中的地位,把“力的分解”作为牛顿运动定律解决问题的一个环节来处理,它是牛顿运动定律解决问题过程中的一个大链条中的小环节。在用牛顿运动定律解决问题时,通常是先选择研究对象,再进行受力分析,由F=ma列出物体受力与加速度等关系的方程,在列平衡方程时,如果有两个力不在同一条直线上,那么运用“力的分解”把力根据需要进行分解。这样捋清主干,会使学生的解题思维更加清晰。正确把握这一节内容的教学目标大大减轻了这一节教学的难度和学生的学习负担;同时也促进了知识在学生头脑中更加系统的、组块化的建构。
3 值得商榷的传统“力的分解”教学过程
在物理教学过程中,要把物理核心素养贯穿到教材中,也就是把物理观念、科学思维、科学探究、科学态度与责任四个方面有机融入到教学中,就要从整个大的框架结构中来认识各个知识的功能、地位和它的要求与内容。
传统的“力的分解”教学过程是用力的分解来求解物体的受力问题,首先“根据力的作用效果”来判定分力的方向,然后用平行四边形定则根据之前判断的分力方向进行力的分解以求分力的大小。但这样的讲解过程值得商榷。
例如,竖直墙壁上用细绳悬吊着的一个小球处于静止状态,试将球所受到的重力G进行分解(如图3)。
如果按照“力的作用效果”对悬吊的球所受的重力G进行分解,那么悬吊的球由于重力作用产生了两个效果,一个是拉绳子的效果,另一个是挤压墙面的效果。因此,可以把重力按“力的作用效果”分解为沿绳子向下的拉力T和垂直墙面的压力N。
那么,这将带来以下疑问:
首先是力的合成中合力与分力的定义:当一个物体受到几个力的共同作用时,常常可以求出这样一个力,这个力产生的效果跟原来几个力共同作用的效果相同,这个力就叫做那几个力的合力,原来的几个力叫这个力的分力。定义中特别强调两次作用是作用在同一物体上产生的效果,第一次作用在这个物体上,第二次仍然作用在这个物体上,只有两次都作用在同一物体上,才可以判断其作用效果是否相同。然而,此处“根据力的作用效果”将重力分解为两个分力,一个是拉绳子的力T作用在绳子上,另一个是挤压墙面的力N作用在墙面上,而重力G是作用在球上的。分力和合力是指同一个物体上两次受力的等效替换,但T、N和G并不作用在同一个物体上。那么,一个力分解成两个力,这两个分力可以分别作用在其他物体上么?如果可以,那么这与上述合力与分力的概念相左;如果不可以,那么显然这样的分析错了。
且根据力的性质可知:G是引力,T和N是弹力;一个引力可以分解为两个弹力吗?这又是一个值得讨论的问题。
由上述例子可知,用“力的合成与分解分析物体的受力问题”在知识的前后逻辑上是存在矛盾的,教材的修改意图是值得教师仔细研读、推敲的。力的合成与分解作为一个有机的整体,在知识结构上体现为统一性,即一种“等效替换”的思想;从内容逻辑上看,教材编写“力的分解”在“力的合成”之后,体现了分解是合成的逆过程,二者是辩证统一的[3]。但“根据力的作用效果”对力进行分解是对这种“等效替换”关系的异化与错误认识。笔者查阅了“力的分解”相关文献的教学设计,仍有不少教师在讲授过程中沿用“根据力的作用效果对力进行分解”的方法[4]。那么,为什么会造成这种知识表述和理解上的错误?且这种对力的错误认识仍在沿用呢?其根本原因就是在教师的头脑中没有物理观念这样一种清晰的认识;教师对“力的分解”这一节内容在整个教材中的地位把握模糊。
从高中物理课程标准和人教版教材的相关修订可以看出:“力的分解”这一内容,它不是用来求解某个物体的受力的一种方法,而是基于整个“运动与相互作用观”下解决问题过程中的一个环节,突出的是它的工具性作用。求解物体的受力,求绳子的拉力T和墙面的压力N等,它不是“力的分解”这一节的教学任务,而是“共点力平衡”和“牛顿第二定律”中的教学任务,在讲共点力平衡时,才需要根据正交分解法来求解上述例子中的问题。
教师在讲授“力的分解”时,将这类例题作为这节内容的课后作业,说明教师将“力的分解”作为“运动与相互作用观”下解决问题的主线,这种处理显然是不合理的。
4 利用几何画板辅助“力的分解”教学
“力的分解”遵循平行四边形定则。若没有其他条件限制,一个合力可以分解为无数对大小、方向不同的分力。通常我们在教学中讨论的都是有一定条件限制的合力分解有定解的情况。简单地说就是代表合力的对角线与给定的代表分力的有向线段是否能构成平行四边形(或三角形)的问题。传统教学中采用粉笔板画对这一内容进行讲解,教师常常需要根据条件的不同,在同一个图中不同的位置准确作图。这势必会造成多条图线相互干扰,在讲解过程中费时费力。
几何画板是一款易学易用、数理性极强,能为广大数学教师和物理教师提供通用的数学、物理学习环境的袖珍软件,它的突出特点之一就是能够即时演示动态的几何关系,同时还具有“矢量图”的体积小、清晰度高、易拆分和组合、组建图形库资源等优点[5]。此时,如果能够充分利用几何画板的动态显现和矢量性功能,则能够在教学中充分为学生创设情境且准确地表达各物理量间的几何关系,起到事半功倍的效果。
下面就力的分解中常见的四种情况,通过几何画板制作课件辅助教学进行简单介绍。
(1)已知合力F和两个分力F1、F2的方向,求F1、F2的大小。此时有唯一解(如图4)。
(2)已知合力F和一个分力F1的大小和方向,求另一个分力F2的大小和方向。此时有唯一解(如图5)。
(3)已知合力F和两个分力F1、F2的大小,求F1、F2的方向。此时有两解(如图6)。
(4)已知合力F和分力F1的方向、分力F2的大小,求分力F1的大小和分力F2的方向(如图7)。当F2=Fsinθ时,有临界值;当F2<Fsinθ时,无解;当Fsinθ<F2<F时,有两解;当F2≥力的作用效果时,有唯一解。
可见,通过几何画板制作课件辅助“力的分解”的教学,能够有机地结合理论分析,为学生呈现清晰、标准的矢量图形,同时能够将解题过程动态显现出来,也大大节约了有限的课堂时间,提高了效率。
5 结 语
由以上“力的分解”教学可以洞见,如何把核心素养真正贯穿于教学,真正渗透到课堂中去,需要广大一线教师重新出发,站在更高的角度仔细研读教材,领会教材修改的意图,正确把握高中物理核心素养基本理念,才能切实地从物理学科的本质出发,培养学生的物理核心素养,满足学生终身发展的需求。
参考文献:
[1]张大昌.普通高中课程标准实验教科书物理(必修1)[M].北京:人民教育出版社,2007:7.
[2]张大昌.普通高中课程标准实验教科书物理(必修1)[M].北京:人民教育出版社,2010:6.
[3]钟传播.“力按效果分解”的深度探析[J].湖南中學物理,2015(8):91-93.
[4]宋丽飞.立足学生实验探究,提升物理核心素养——以“力的分解”为例[J].中学物理教学参考,2018,47(6):25-26.
[5]周新雅,王惠玲,周行.用几何画板创设“光的反射”教学情境[J].物理通报,2018(9):100-103.
(栏目编辑 赵保钢)

