浅谈正方形综合题命制思路

杨文川

[摘  要] 文章讨论了在正方形背景下重庆中考数学几何综合题命制的基本思路，基于正方形与翻折运动结合，主要研究翻折方向的选择、初中重要几何性质的引入、学生运算能力的考查等几个方面.

[关键词] 重庆中考数学;正方形;翻折;几何性质;运算能力

引言

在近几年的重庆中考数学几何综合题命制中，以正方形为背景的综合题往往是考查的热点之一. 正方形包含了所有特殊平行四边形的基本性质，对于学生掌握初中数学几何性质非常重要. 基于正方形和翻折运动相结合的综合题，往往出现在重庆中考题的18题，此题具有图形结构复杂、辅助线添加困难、解题思路多样、运算量大等特点. 例如：

考题1：（2017重庆）如图1，正方形ABCD中，AD=4，点E是对角线AC上一点，连接DE，过点E作EF⊥ED，交AB于点F，连接DF，交AC于点G，将△EFG沿EF翻折，得到△EFM，连接DM，交EF于点N，若点F是AB边的中点，则△EMN的周长是______.

考题2：（2016重庆）如图2，正方形ABCD中，对角线AC，BD相交于点O，DE平分∠ADO交AC于点E，把△ADE沿AD翻折，得到△ADE′，点F是DE的中点，连接AF，BF，E′F.若AE=，则四边形ABFE′的面积是______.

因此对于此类题型的研究非常重要而且很有必要，下面我们将从几个方面进行分析.

选择翻折方向

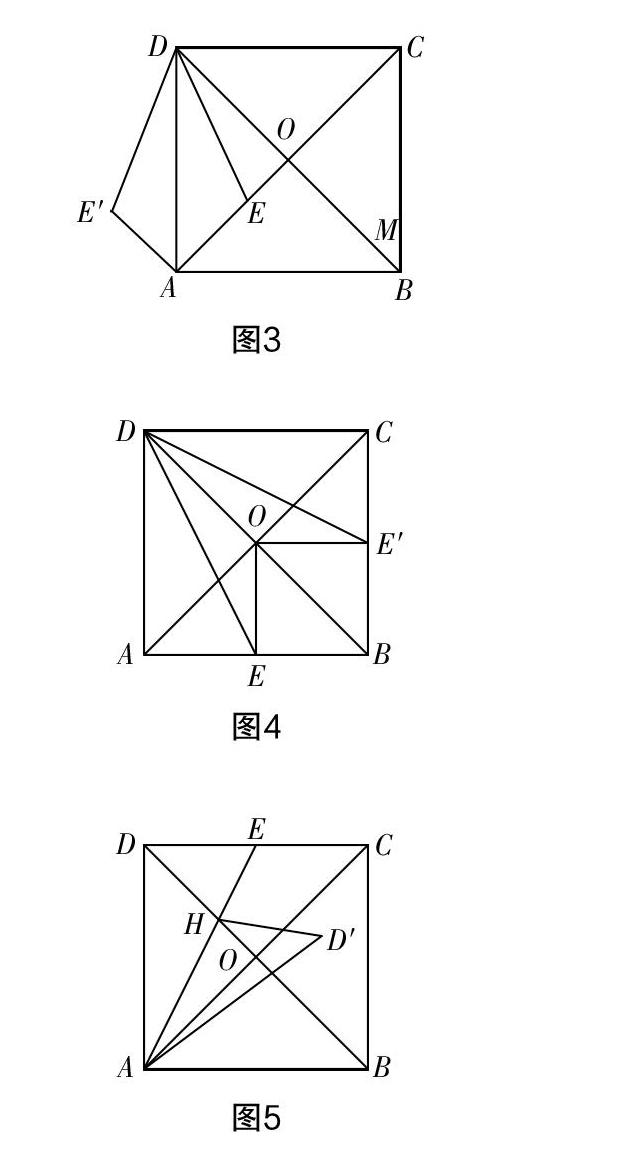
在正方形与翻折运动的结合中，往往会将三角形延着重要线段翻折，线段主要是正方形的边、对角线、特殊点连线（例如：顶点和中点连线）. 当选好线段后，接下来要考虑翻折的方向，不同的方向会产生出形内图和形外图两种基本组合图形，如图3～图5.

其中，图3是将△AED延着AD翻折产生了形外图△ADE′，图4是将△OED延着对角线BD翻折产生形内图△ODE′，图5是将△AOD延着AE（E点为DC中点）翻折产生形内图△AOD′. 因为翻折方向具有多变性，这里不再一一举例.

引入几何性质

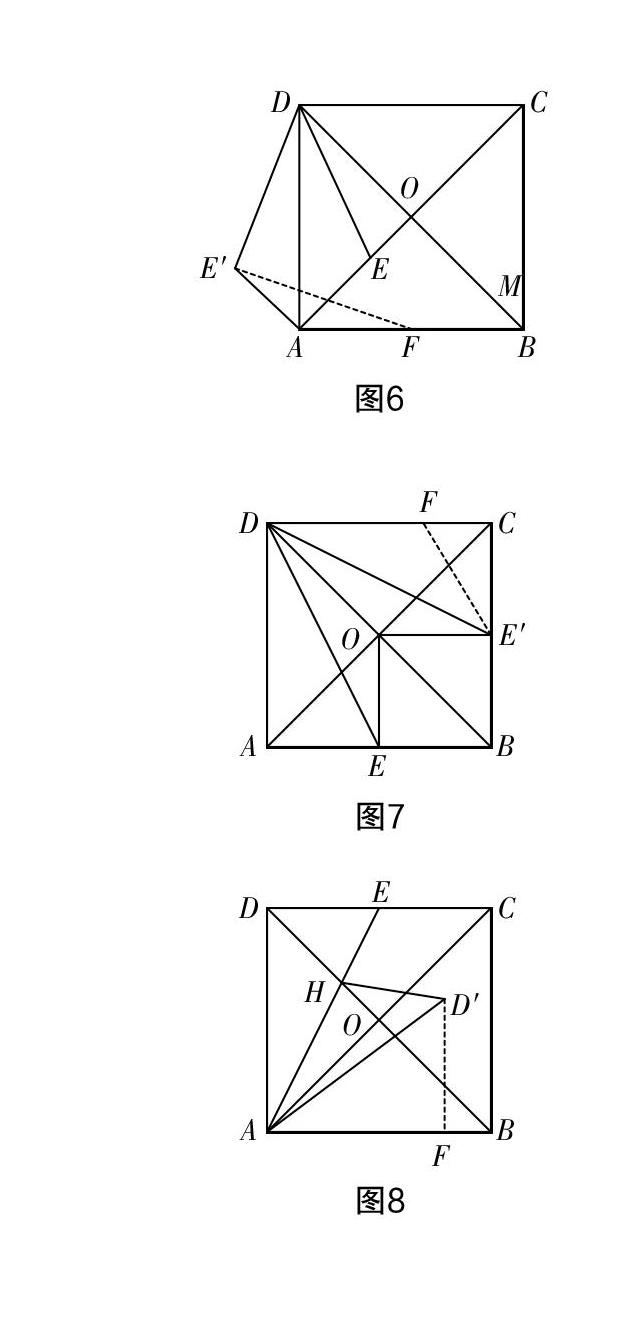
翻折结束后，将从两个方向引入几何性质. 第一，组合图形自身产生. 首先，翻折本身具有不变性，因此翻折前后对应图形的边、角、高线、角平分线、中线的大小都不会发生改变，因此原有图形的几何性质可以作为考查对象. 其次，对称轴本身就是角平分线. 例如图3，AD平分∠EDE′. 第二，“无中生有”，此种方法往往是考查重点. 主要是添加条件产生新的点或者线段，从而考查几何性质，如图6～图8.

其中，图6增加AB的中点F，图7是增加∠DE′C的角平分线交DC于F点，图8是过D′作AB的垂线交AB于F点. 三种方式就分别引入了中点、角平分线、垂线. 因为增加方式多种多样，而且可以选择的边、角也不同，这里不再一一举例.

设计解题思路

当图形结构固定后，设计运算是最后一步也是最难的一步，因为学生层次不同，能力差异很大，部分同学超前学习知识，运算能力强;部分同学知识结构单一，求解方法简单. 因此设计出一条既能考查学生解题能力，又能包含重要知识内容的解题思路就非常重要. 解题思路设计一般分为以下几个步骤：

第一，告诉边长或者已知线段长度（例如2016、2017重庆中考18题）. 这样学生就有一个突破口，沿着出题人设置好的线路寻找解题思路.

第二，在图形中分析隐含条件，帮助求解. 这一步是最困難的一步，分析有用的隐含条件是考查学生建模思维、抽象思维的重要环节. 例如图6中连接OF，则OF是△ABD的中位线;图7中CF是△DFE′中以DE′为边的高;图8中三角形AFD′三边之比为FD′ ∶ AF ∶ AD′=3 ∶ 4 ∶ 5.

第三，设置问题. 问题的设置往往是告诉学生“去向何方”，一般设置的问题分为求线段、角、三角形面积、三角形周长、三角形的中线、高线、角平分线等等，有时也可以求解四边形周长、面积. 例如图6我们可以求解E′F的长度，图7我们可以求解△DFE′的面积，图8我们可以求解四边形AHD′F的周长.

第四，验算. 这一步往往是检查求解过程中有无超纲知识点，答案是否合理，运算是否烦琐等.

重庆中考数学的几何考查一直是学生的难点之一，本文给出了正方形综合题命制的基本思路之一，因为图形结构具有多变性、解题思路具有多样性、学生能力具有差异性等特点，这个问题还有很多值得探讨的地方，待其他老师继续研究讨论.