改进粒子群优化BP神经网络短期负荷预测研究

王 瑞，周晨曦，逯 静

（1.河南理工大学 电气工程与自动化学院，焦作 454000；2.河南理工大学 计算机科学与技术学院，焦作 454000）

0 引言

BP神经网络有着较为良好的非线性映射能力、高度的自适应自学习能力、良好的泛化能力，以及容错能力的优点被应用于电力负荷预测中[1,2]，同时也存在着容易陷入局部极小值、收敛速度慢的缺点，对BP神经网络的改进已经成为学者们研究的热点，比如调整自适应学习速率[3]、改进网络结构[4]、引入优化算法[5～7]等。利用粒子群优化BP神经网络是一种较为常用的方法，利用粒子群优化BP神经网络，可以有效防止BP神经网络陷入局部最优，并加快其收敛速度。基本粒子群算法寻优速度较快、效率高、算法简单，但也存在自身的缺陷，当算法迭代时，所有粒子都向当前自身最优解、邻域或群体最优解移动，种群搜索空间不断缩小，形成种群快速趋同效应，而此时的最优位置可能只是某一局部搜索空间里的最优位置，搜索陷入局部极值之中，导致早熟收敛，后期种群的多样性难以维持。对此学者们也提出了很多改进方法[8～11]，在文献[8]和文献[9]中分别提出粒子群结合差分进化算法、粒子群结合遗传算法的方法，使粒子在搜索过程中，拥有交叉和变异功能，提高粒子种群的多样性，避免陷入局部极优，但此种方式可能使优良粒子也发生变异导致丢失优越位置寻优效率变差。文献[10]提出粒子群结合万有引力搜索算法以提高算法的搜索能力，文献[11]提出通过动态改变惯性权重自适应粒子群算法以平衡全局搜索和局部搜索的性能，但这两种方式均未能改变种群粒子易丧失多样性的缺点。

在本文中引入了平均适应度值，在每次粒子群体迭代过程中，评价每一粒子适应度值，求出群体适应度平均值，对于每一粒子适应度值与群体平均适应度值相比较，当粒子适应度值劣于群体平均适应度值时，对其空间位置初始化处理，随机生成新的位置，当优于或等于种群平均适应度时，保持位置不变，通过此种方式，不仅保留了种群中优良粒子，而且增加了种群在空间中全局搜索能力，保持了种群多样性，提升了粒子群搜索性能，可以有效提升BP神经网络短期电力负荷预测精度。

1 基本粒子群优化模型

粒子群优化算法是由Kennedy博士和Eberhart博士于1995年提出的基于仿生的集群优化算法。其原理为：在粒子群算法中，每个优化问题的解都是搜索空间中的一个粒子，每个粒子都有自己的位置、速度和一个被优化的函数决定的适应值，这些粒子在解的空间中追随当前的最优粒子进行搜索。每次迭代中，每个粒子通过两个最优解更新自己的位置：一个是粒子本身所找到的最优解，称为个体极值，用pbest表示，另一个是当前整个粒子群中的最优解，即全局极值，用gbest表示。在多维空间中其维数由组成解的参数数量决定，BP神经网络中的参数数量即是粒子群空间维数。

粒子更新自身速度的公式为：

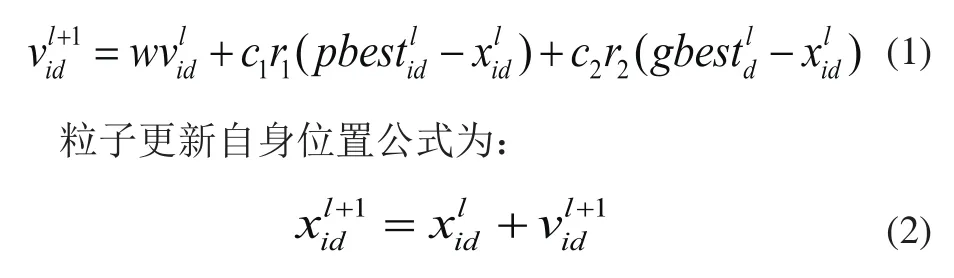
式中w表示惯性权重，c1和c2为学习因子，r1和r2表示在[0，1]之间的随机常数，vl+1id和xl+1id分别表示第i个粒子在第l+1次迭代中第d维的速度和位置；分别表示第i个粒子在第l次迭代中第d维的速度和位置；pbestid表示第i个粒子在第d维的个体极值；gbestd表示群体在第d维的全局极值。

2 BP神经网络模型

BP神经网络为输入层、隐含层、输出层三层结构。其结构如图1所示。

图1 BP神经网络

在BP神经网络中，设输入层节点数为M，输出层节点数设为N，隐含层神经节点由经验公式确定[10]，其形式如下：

其中P为[1，10]内的任意值，L为隐含层节点数。

设ti为输入层节点i的输入变量；Wih表示输入层节点i与隐含层节点h的连接权值；bh表示隐含层节点h的阈值；φ(x)表示隐含层激励函数；Who表示隐含层节点h与输出层节点o的连接权值；BO表示输出层节点o的阈值；ψ(x)表示输出层激励函数；

隐含层节点h的输入为：

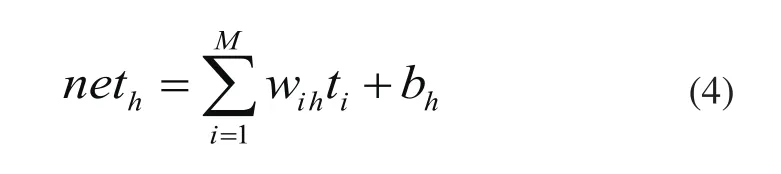
隐含层激励函数为Sigmoid函数，隐含层节点h的输出为：

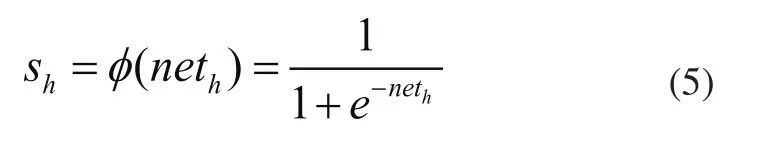
输出层激励函数ψ(x)为纯线性函数，每一节点输入和输出相同：

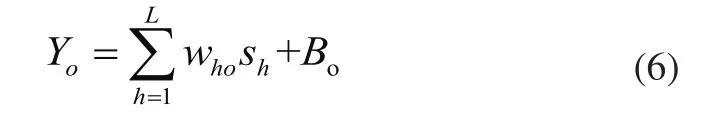
YO为输出层节点o预测输出值。

3 改进PSO算法优化BP神经网络模型

用改进的PSO算法优化BP神经网络，其具体步骤如下：

Step1：对于BP神经网络，确定BP神经网络结构、学习速率、目标精度、训练次数。对于粒子群算法，确定种群规模、迭代次数、学习因子、惯性权值、位置和速度的限定空间、并依据BP神经网络参数个数确定粒子群的维数。

Step2：按照建立的BP神经网络模型，随机生成粒子群Ti=（Wil，wi2，…，Win）T，i=1，2，…，m，作为神经网络参数初始值，其中：

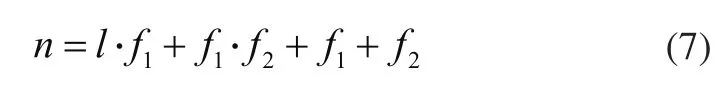
n为粒子群搜索空间维数，l为输入层节点数，f1为隐含层节点数，f2为输出层节点数，m为种群粒子数目。

Step3：将Step2中粒子Ti，对BP神经网络各个参数赋值，之后利用训练样本训练BP神经网络，达到设定精度后得到网络中第K样本节点o训练输出值CO(k)，则在种群T中个体Ti的适应度 fi tnessi定义为：

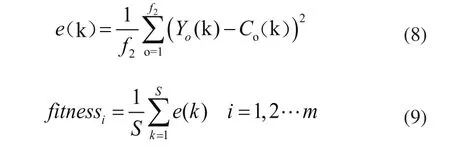
其中，YO(k)第k样本节点o实际输出值，S为总体样本数，m为种群规模。

Step4：计算每一粒子Ti对应的适应度值，这里的适应度值就是误差值，适应度值越小越好，确定初始种群的个体最优值，全局最优值。

Step5：计算种群平均适应度值，对每一粒子适应度值与种群平均适应度值比较，如果粒子适应度值小于或等于种群平均适应度值则保持状态不变，如果粒子适应度值大于种群平均适应度值则将粒子位置初始化。

Step6：计算新粒子的适应度值，更新粒子群体个体极值与全局极值。

Step7：在每次迭代中先按照式(1)和式(2)更新粒子速度和位置，再计算适应度值、新粒子个体极值、种群全局极值，然后按照Step5、Step6对粒子群更新，不断循环迭代，直到满足迭代次数，将种群最优粒子对BP神经网络的初始权值与初始阈值赋值。

图2所示为改进粒子群优化BP神经网络程序实现流程图。

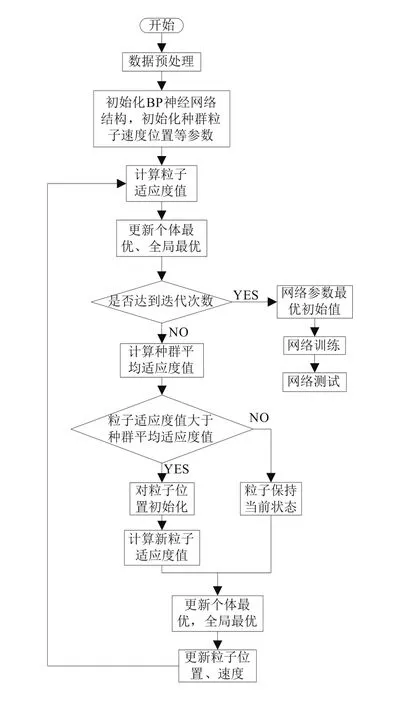
图2 改进粒子群优化BP神经网络流程图

4 数据处理与预测模型参数设置

在对电力负荷预测时，会受到多种因素的影响比如气候、日期类型、市场、经济、政治、所在地区的地理位置等。对于不同的地区每一因素对于电力负荷的影响程度不同，本文是对河南省某地区的电力负荷预测，综合考虑该地区的特点，得出对电力负荷影响程度明显的因素为日最高气温、日最低气温、预测时刻气温、星期类型和节假日。从该地区电力公司采集2017年春季70天的负荷数据，并获取记录的日最高气温与日最低气温，以及每一时刻气温。

4.1 对影响因素的处理

对于影响电力负荷的因素，由于无法比较它们之间的差异度，需要把各个特征因素映射到特定的数值区间使各个量之间有了数值上的可比性[13，14]，同时能够在BP神经网络中训练以及预测，在分析周日与节假日的映射值时将两者划归为一类，映射关系如表1所示。

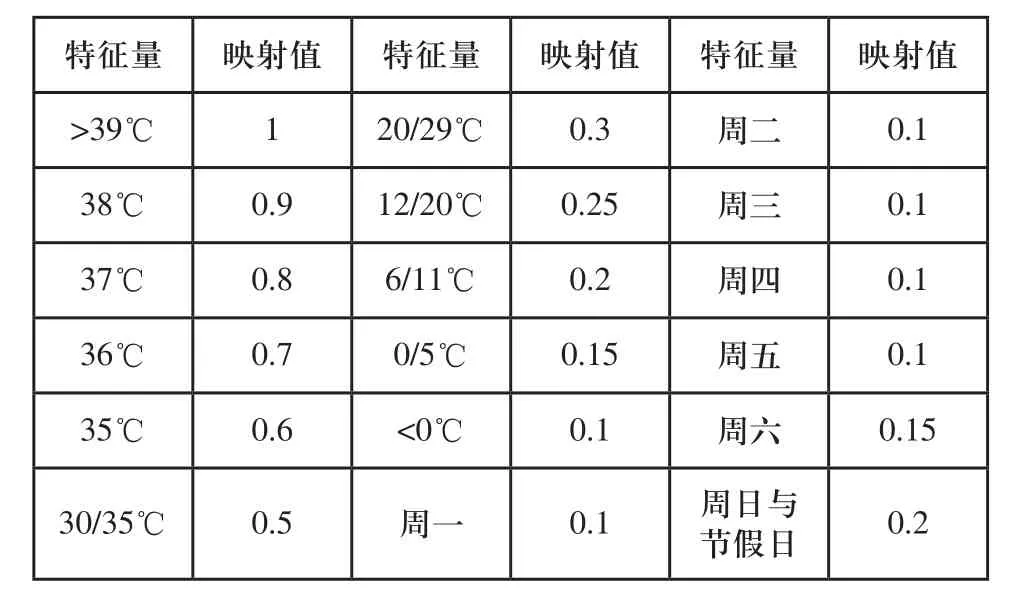
表1 特征量映射表

4.2 对BP神经网络模型设置

用BP神经网络预测前先对负荷数据进行归一化处理，对于24个时段每一时段为一类，对每一类数据都归一化[15]，公式如下：

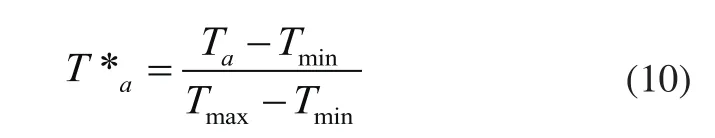
T*a为某一时段中的负荷Ta归一化后的数据，Tmin，Tmax表示此类负荷数据的最小值与最大值，得出预测值再逆还原。

对于预测日是对每一时刻的负荷预测，按照每天24个时间段分为24个BP神经网络模型分别预测。BP神经网络负荷预测输入与输出节点描述如表2所示。

表2 BP神经网络节点表述表

在表2中，Xn-1表示预测日前一天对应时段的归一化负荷数据；Xn-2表示预测日前两天对应时段的归一化负荷数据；Xn-7表示预测日前一周对应时段的归一化负荷数据；TDn表示预测日预测时刻气温映射值；TLn表示预测日当天的最低气温映射值；THn表示预测日当天的最高气温映射值；Wn表示星期类型映射值，其中国家法定节假日和周日为同一类作为休息日；Yn表示该时段实际输出的归一化负荷值。

对每一网络参数设置：依照表2，BP神经网络输入层有7个节点，输出层有1个节点，依照经验公式(1)，可设隐含层有12个节点。对网络参数值随机设定[0，1]之间的任意值，神经网络训练次数为100，训练目标精度为0.0001，学习速率设为0.05。

4.3 对改进PSO-BP神经网络模型参数设置

对于BP神经网络部分设置同上，对改进PSO部分参数设置：种群规模为150，进化次数为500，学习因子为C1=C2=1.459445，粒子位置限定范围为[-1，1]，速度限定范围为[-0.1，0.1]，惯性权重采用线性递减策略，从0.9随迭代次数依次递减至0.4如下式所示：

wmax为最大权重，wmin为最小权重，kmax为最大迭代次数。

标准PSO-BP神经网络模型参数和改进的PSO-BP神经网络模型参数一致。

4.4 预测性能指标

预测性能指标有三种，其一为最大绝对误差（MAXAE），其二为平均绝对误差（MAE），其三为平均相对误差（MRE）。三种类型公式如下：

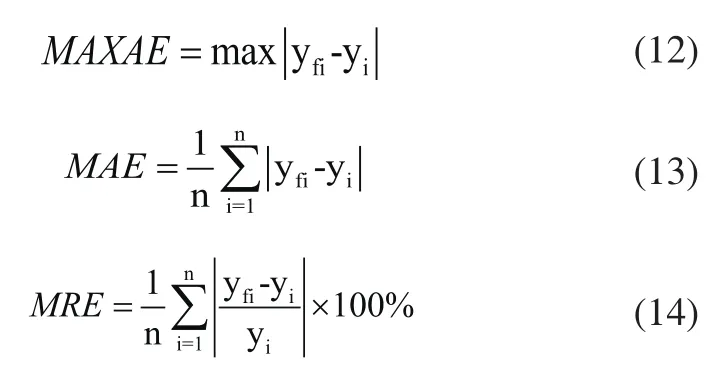
其中，yf为预测值，y为实际值，单点预测误差为实际值减去预测值。

5 实验分析

为了验证提出的改进粒子群算法优化 BP神经网络（IPSO-BP模型）的有效性，将其与基本粒子群优化BP神经网络模型（PSO-BP模型）、BP神经网络模型（BP模型）用相同的数据训练，并对同一天电力负荷预测，通过预测结果比较三种模型之间的优劣。

三种预测模型均在Matlab R2014b平台中程序实现，利用采集的前67天的负荷数据训练各个网络模型，并对第69天的负荷预测。图3为BP模型预测值与实际值对比图，图4为PSO-BP模型预测值与实际值对比图，图5为IPSO-BP模型预测值与实际值对比图，图6为三种模型预测误差值对比图。

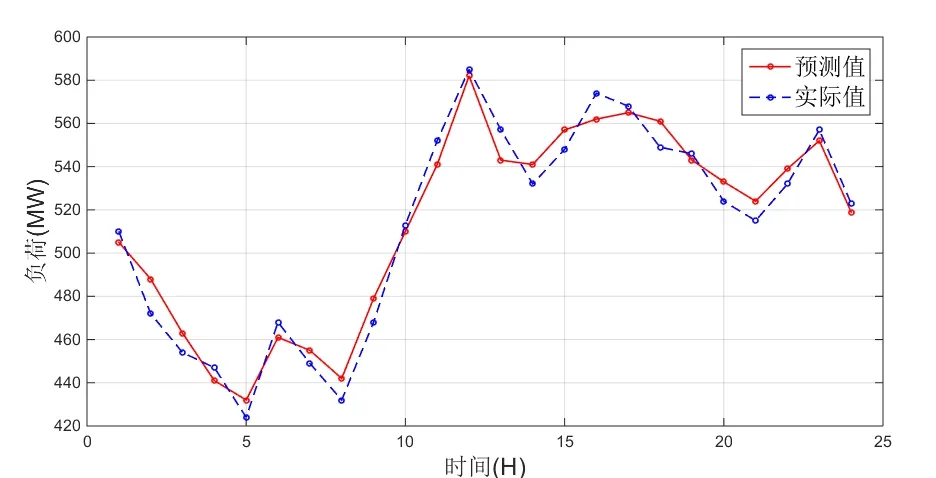
图3 BP模型预测值与实际值对比图

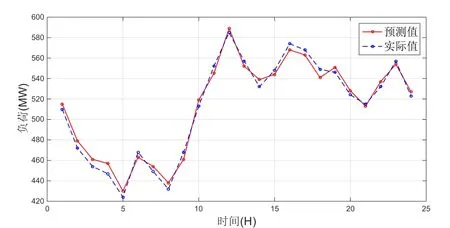
图4 PSO-BP模型预测值与实际值对比图

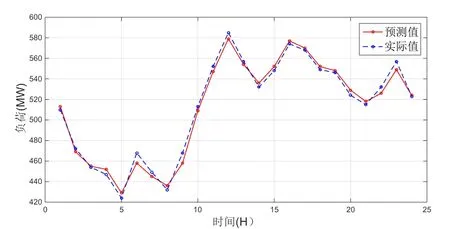
图5 IPSO-BP模型预测值与实际值对比图

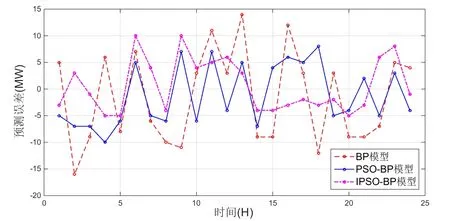
图6 预测误差对比图

从图3、图4、图5可以看出，三种预测模型都能够较好的预测电力负荷。从图6预测模型误差对比图可以看出，IPSO-BP模型相比于其他两种模型整体各点误差更接近0值。

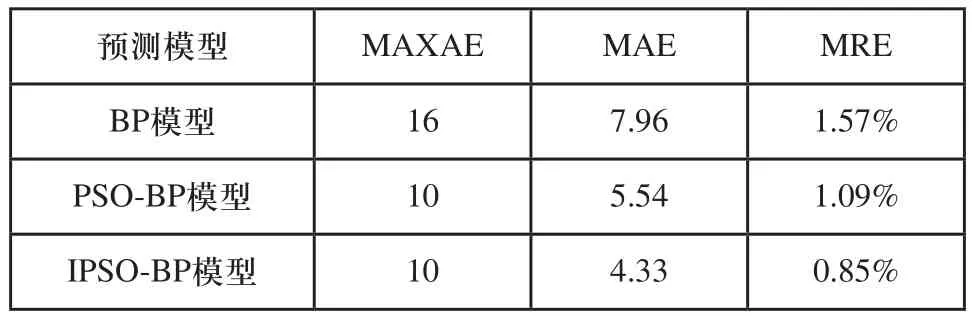
表3 模型预测结果比较表

在表3中，结合最大绝对误差，平均绝对误差，平均相对误差三种预测性能指标，可以看出IPSO-BP神经网络比其他两种预测模型有着较好的预测性能，这是因为改进的粒子群在迭代过程中没有形成快速的趋同效应，在迭代的后期依然保持种群多样性的特征，避免陷入局部极优，扩大了搜索空间，增加了寻得全局最优值得概率，所以其预测精度高于PSO-BP模型和BP模型。

6 结束语

本文提出的改进粒子群优化BP神经网络模型，解决了BP神经网络模型收敛速度慢、迭代过程中易陷入局部极小值问题，以及解决了基本粒子群算法易陷入局部极优值的问题。将其应用于短期电力负荷预测中并与基本粒子群优化BP神经网络模型和BP神经网络模型的预测结果相比较，结果表明：相对于基本粒子群优化BP神经网络模型、BP神经网络模型该方法有着更高的预测精度。