滑移门保持件结构布置多目标优化*

周巧英，薛志刚，周五峰，林启权，李落星

（1.湘潭大学机械工程学院，湘潭 411105； 2.湖南大学，汽车车身先进设计制造国家重点实验室，长沙 410082；3.重庆长安汽车欧尚研究院，重庆 400023）

前言

近年来，配置了滑移门的MPV车型由于开门空间小、进出方便、结构稳定等优点，使其在市场上占有率逐步提高。碰撞事故统计表明，当汽车发生侧撞或急速转弯时，乘员与车门产生剧烈撞击，乘员伤害很大部分是由于车门与车身连接可靠性较差引起的［1］。为减少此类事故的发生，2013年强制实施的国标GB15086—2013除了在横向向外载荷作用下，导轮不得从导轨中脱开之外，还增加了车门与门框分离距离和施力装置总位移量的要求［2］。该法规的实施在提高整车被动安全性的同时也带来了法规一次性通过率低、试验成本增加的问题。

汽车的滑移门通过某些零部件与车身连接，这些零部件一般称为保持件，它们包括滑移门的导轨和其它支撑零件。目前，国内外对滑移门保持件性能的研究主要集中在加强件结构改进和壁厚优化方面。文献［3］～文献［5］中对滑移门保持件附近加强件的结构进行改进，使车门与门框的最大分离距离显著减小，保持件性能满足法规要求。文献［6］中采用灵敏度分析方法对滑移门保持件周围加强件的壁厚重新分配。结果表明，保持件性能在满足国家标准要求的同时实现了轻量化设计。滑移门保持件的结构布置往往受到车型定位和造型的限制，在限制范围内，合理设计滑移门保持件的结构布置能显著提高保持件性能，为乘员在车辆行驶过程中的人身安全提供保障。

但是，有关滑移门保持件结构布置对保持件性能的影响，以及将结构布置与多目标优化相结合的研究报道较少见，本文中基于试验验证的仿真模型，以中导轨、挂钩和后锁高度方向距离为设计变量，采用最优拉丁超立方试验方法和RBF神经网络模型建立最大分离距离的近似模型，以车门与门框最大分离距离最小为优化目标，中导轨、挂钩和后锁高度方向距离的变化范围为约束条件，采用NSGA-II算法对保持件结构布置进行多目标优化。

1 滑移门保持件试验与性能要求

GB15086—2013对汽车滑移门保持件试验方法做了详细规定。

1.1 试验方法

图1 滑移门保持件试验加载示意图

（1）滑移门保持件性能试验装置如图1所示。以20～90 mm／min的速度移动图1中的两个施力装置，直到每个施力装置达到9 000 N的力或300 mm的总位移量。

（2）如果一个施力装置比另一个施力装置先达到9 000 N的目标力，则先达到的施力装置继续保持9 000 N的力，直到另一个施力装置也达到9 000 N的目标力。

（3）如果两个施力装置都达到9 000 N的目标力，保持该目标力至少10 s。

（4）施力装置保持规定的载荷，测量车门和门框之间的最大分离距离。

1.2 评价标准

车门与门框的最大分离距离小于100 mm；任何一个施力装置的总位移量小于300 mm；所有导轮不得从导轨中脱开。

选择一辆带有左前车门和滑移门系统的白车身，去除所有对试验安装和操作有妨碍的座椅、内饰、装饰部件等。在前后轮毂包处纵梁的外表面增加固定约束挡板（前右轮毂包除外），将试验车固定在地面上，同时，将试验装置和支撑部件安装并固定在法规要求的位置。确保所有车门保持件锁紧时，以50 mm／min的速度加载，在达到9 000 N的载荷或300 mm的位移量之后保压10 s。试验允许导轮从导轨中脱开和最大分离距离超过100 mm的法规要求，但当加载板的位移量超过300 mm时需立刻停止试验，以免滑移门脱落对试验人员造成伤害。试验中通过直尺测量车门与门框的最大分离距离，通过位移传感器测量加载装置的载荷-位移曲线。

2 滑移门保持件性能试验与仿真分析

2.1 保持件性能试验

图2 最大分离距离试验结果

根据法规要求的边界条件，在试验车上进行滑移门保持件性能试验，试验结果如图2和图3所示。由图可知，在规定载荷下车门与门框上端和下端最大分离距离分别为150.1和135.2 mm，超过100 mm的国家标准要求；中导轮从导轨中脱开；由位移传感器获得B柱和C柱侧加载板的总位移量分别为125.3和202.5 mm；试验结果不满足法规要求。

图3 中导轨与导轮相对位置试验结果

2.2 仿真建模

白车身和车门主要采用薄壳单元QUAD4和TIRA3对几何模型进行网格划分，单元尺寸为8 mm，锁体／锁扣、轮臂、导轮采用的是HEX8和PENTA6单元，单元尺寸为2 mm。此外，根据实际受力情况，对集中受力区域的网格局部细化。模型包含263 292个单元，其中QUAD4单元221 613个，TIRA3单元7 777个（占单元总数的2.95%）。白车身、车门各钣金件之间的点焊和胶粘均采用Solid实体单元模拟。模型各部件间的连接严格按照实物之间的连接关系，分别采用螺栓、铰链、胶粘、点焊和缝焊模拟。滑移门保持件的有限元模型如图4所示。

图4 滑移门保持件有限元模型

根据法规要求，有锁体／锁扣一侧，在锁芯同一水平位置的车门内板外边缘沿车辆横向施加9 000 N的载荷，加载板的尺寸为150 mm×50 mm×1 mm；无锁体／锁扣时，载荷施加在整个车门内板中间点的外边缘，加载板的尺寸为300 mm×50 mm×1 mm。采用弹簧加载的方式在远离车门一侧的加载板1和加载板2上施加9 000 N载荷，达到法规规定的载荷或靠近车门侧加载板的总位移量达到300 mm时保压10 s，测量车门与门框的最大分离距离，加载位置和加载板的尺寸如图5所示。

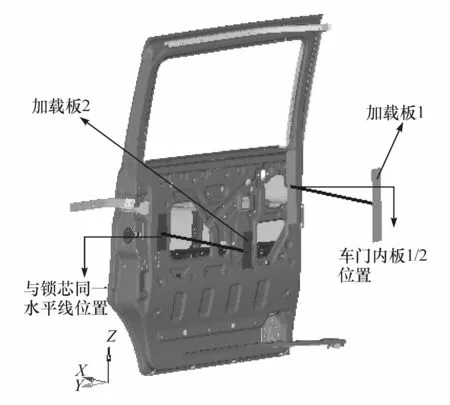
图5 仿真分析加载示意图

根据试验状态，全约束前后轮毂处的纵梁（前右轮除外），约束区域为50 mm×100 mm，同时在白车身与地板接触位置增加两块不变形的薄钢板，以模拟地面，约束区域如图6所示。试验的加载速度为50 mm／min，加载速度较缓慢，是一个典型的准静态加载；仿真加载速度为1.2×105mm／min，采用快速加载的方式缩短计算时间，为减小材料应变速率对仿真结果的影响，材料曲线只输入准静态条件下的应力 应变曲线。

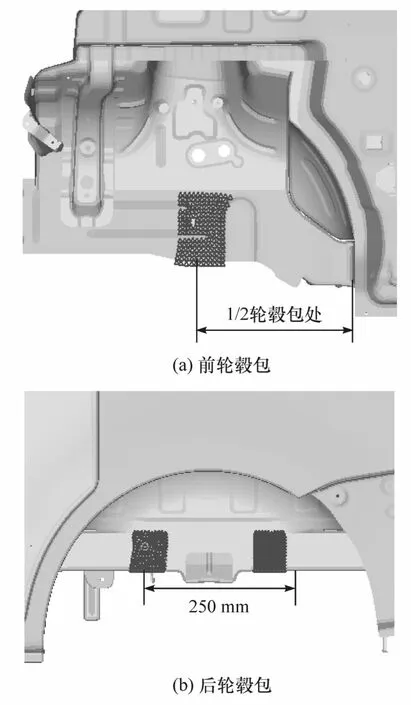
图6 仿真分析约束示意图

2.3 仿真结果分析

将滑移门保持件仿真模型提交LSDYNA软件进行计算，结果如图7～图9所示。由图可知，车门与门框上端和下端最大分离距离分别为156.52和147.67 mm，与试验结果的误差分别为4.1%和8.44%；中导轮从导轨中脱开；B柱和C柱侧加载板的总位移量分别为133.06和215.01 mm，仿真与试验的误差分别为5.12%和3.58%。

图7 最大分离距离仿真分析结果

图8 中导轨与导轮相对位置仿真结果

表1为滑移门保持件性能试验与仿真结果对比。其中，Su和Sl分别为车门与门框上端和下端最大分离距离，SB和SC分别为B柱和C柱侧加载板的总位移量。由表可知，仿真与试验结果的性能评价指标基本接近，误差小于9%，表明该滑移门保持件性能仿真模型精度较高，可用于指导滑移门保持件性能优化工作。

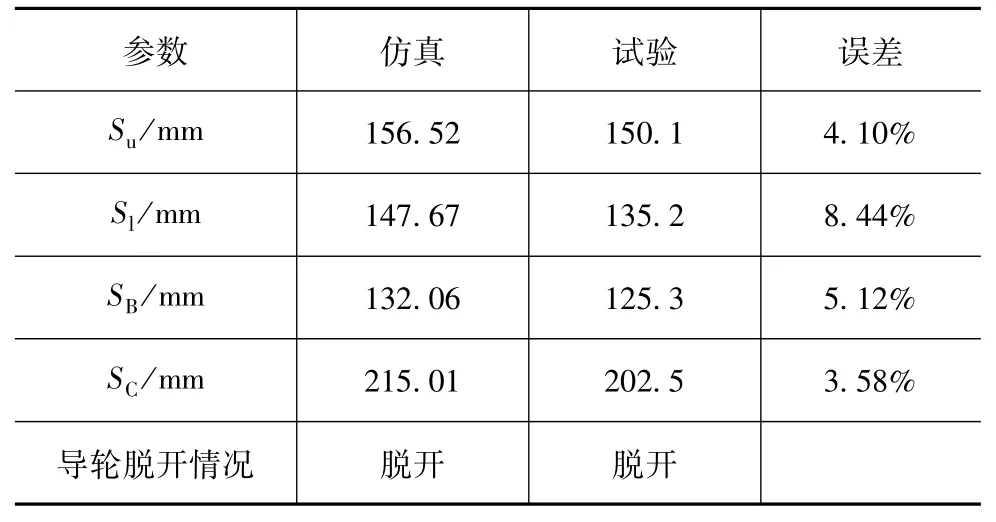
表1 滑移门保持件性能试验与仿真结果对比

3 保持件性能多目标优化

3.1 滑移门保持件位置参数化设计

滑移门通过导轮在3根导轨上的来回运动实现车门的开启和关闭，锁止机构为乘员在行车过程中的安全提供了保障。仿真分析发现中导轨、挂钩和后锁在整个门框上的布置对保持件性能影响较大。中导轨、挂钩和后锁高度方向位置示意图如图10所示，其中，Lf，Lr和Lg分别为挂钩、后锁和中导轨高度方向距门框上边缘的距离。

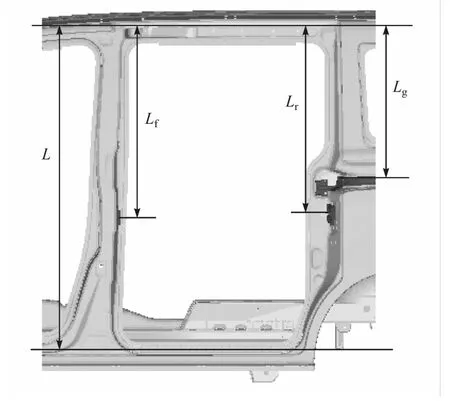
图10 中导轨、挂钩和后锁位置示意图

3.2 最优拉丁超立方试验设计

本文中采用最优拉丁超立方的试验设计。拉丁超立方设计是一种多维分层抽样方法，其最大的优点是能够避免重复抽样，用较少样本点来研究较多因子，但在高维设计空间采样时，可能导致样本点分布不均匀。最优拉丁超立方设计则是在拉丁超立方设计的基础上运用优化算法使样本点尽可能均匀分布在设计空间［7］。常用的优化准则［8-9］为

式中：Y（x）为设计变量响应；fj（x）为第j个设计变量x的函数；k为设计变量个数；αj为待定系数；Z（x）为均值为0的高斯分布函数。

一维输入s与t的协方差函数为

式中：0＜q≤2，参数 θ与q决定了Z（x）的性能，因此，最优优化准则与-lg｜R｜最小等价。

图11为两因素9个样本点的随机拉丁超立方和最优拉丁超立方采样结果对比。本文中采用最优拉丁超立方试验设计方法设计中导轨、挂钩和后锁高度方向的距离矩阵，并进行滑移门保持件性能仿真分析，样本32个。

图11 两因素试验设计采样对比

3.3 RBF近似模型

RBF模型是一种三维前向网络，首先是确定一组样本点，xi=（x1，…，xn），i=1，2，…，n；再以样本点为中心，通过径向基函数的线性叠加来计算待测点响应值。径向基函数把一个多维问题转化为以欧几里得距离为自变量的一维问题，具有容错性好，能消除样本中的“噪声”输入，且逼近任意非线性函数的能力很强［10］。RBF近似模型的基本形式为

式中：y为待测点响应；n为基函数个数；ωi为基函数的权系数；Ф（ri）为基函数；ri为待测点x与样本点xi之间的欧几里得距离。

根据前面采集的最优拉丁超立方样本点数据得到仿真分析结果后，以中导轨、挂钩和后锁高度方向的距离作为设计变量，车门与门框上端和下端最大分离距离作为优化目标函数，采用径向基函数神经网络方法建立符合要求的拟合模型。本文中以确定性系数R2来表征近似模型的逼近程度，其定义为

式中：Qc为残余偏差平方和；Qz为偏差平方和。

拟合模型的精度如图12所示，车门与门框上端Su和下端Sl最大分离距离的确定性系数R2分别为0.961和0.916，说明该近似模型的精度较高，可取代详细模型进行计算。

图12 近似模型实际值与预测值对比

3.4 基于遗传算法的保持件布置多目标优化

滑移门保持件性能评价指标之一是车门与门框的最大分离距离，因此多目标优化以车门与门框上端Su和下端Sl的最大分离距离最小为目标。同时，由于保持件的结构布置受车型定位和造型的限制，以中导轨、挂钩和后锁高度方向距离的变化范围作为约束条件。将中导轨、挂钩和后锁高度方向的距离Lf，Lr和Lg作为设计变量，建立的多目标优化数学模型为

采用第二代非支配遗传算法（NSGA-II）对该数学模型进行迭代寻优［11］。其中，群体规模为16，最大遗传代数为30，而交叉率设置为0.9，共进行了482次迭代。计算得到车门与门框最大分离距离的Pareto前沿曲线，如图13所示。根据前面确定的车门与门框上端Su和下端Sl的最大分离距离最小的优化目标，可以推测，最为接近，即差别最小的Su和Sl将是所要寻找的最优解。据此，通过简单的作图法，不难从图13的诸多Pareto解中找到Su=65.42 mm，Sl=65.99 mm的一个解（对应于优化过程的第150步），故本文中选取该点作为滑移门保持件结构布置的最优解。

图13 车门与门框最大分离距离的Pareto前沿曲线

将基于RBF神经网络模型进行优化得到的最佳结构布置进行规整化处理后，代入滑移门保持件性能仿真模型中计算，优化前后保持件性能对比如表2所示。由表可知，车门与门框上端和下端的最大分离距离分别降至65.42和65.99 mm，导轮始终未从导轨中脱开，且B柱和C柱侧加载板的位移量均小于300 mm，满足法规对保持件性能的要求。

表2 保持件结构布置优化前后性能对比mm

4 结论

（1）建立某标杆车滑移门保持件仿真分析模型，开展基于GB／15086—2013法规的保持件性能试验，验证了滑移门保持件仿真模型的可靠性。

（2）以中导轨、挂钩和后锁高度方向距离为设计变量，采用最优拉丁超立方试验方法和RBF神经网络模型建立车门上端和下端最大分离距离的近似模型，模型的确定性系数R2分别为0.961和0.916，近似模型的精度较高。

（3）以车门上端和下端最大分离距离最小作为优化目标，中导轨、挂钩和后锁高度方向距门框上边缘距离作为约束条件，采用NSGA-II算法对保持件结构布置进行多目标优化。结果表明，上端和下端的最大分离距离分别降低至65.42和65.99 mm，导轮始终未从导轨中脱开，且B柱和C柱侧加载板的位移量均小于300 mm，满足法规对保持件性能的要求。

（4）对滑移门保持件性能进行优化时，未考虑中导轨、挂钩和后锁结构布置变动引起加强件结构改变对性能的影响，且优化方案缺乏试验验证，今后须在这两方面开展后续研究。