铝合金车体的有限元分析和结构评估方法研究*

王万林，徐从昌，王震虎，王哲阳，李落星

（1.湖南大学，汽车车身先进设计制造国家重点实验室，长沙 410082； 2.湖南大学机械与运载工程学院，长沙 410082）

前言

电动汽车的快速发展迫切需要更轻质的车身来弥补因放置电池引起的质量增加，以实现更理想的续航里程。铝合金因其密度小、性能优的特点成为各大汽车厂商青睐的轻量化车身材料［1］。

在铝合金车身的开发应用方面，国外学者已经做了大量研究。从1994年诞生的第一台奥迪A8全铝车身至今，一系列具有代表性的车型如奥迪R8、捷豹XJ、特斯拉Models S和宝马i3的相继问世标志着铝合金车身开发技术的日益成熟。同时形成了3种具有代表性的技术路线：（1）以铝板代替钢板，以自冲铆接和胶粘代替点焊的承载式铝车身结构；（2）以铝型材、板材和铸件各占一定比例的空间框架式铝车身结构；（3）“铝合金下车体＋碳纤维上车体”的车身结构［2-5］。而在国内，车身用铝合金的研究起步较晚，目前更多的体现在零部件级别，如前碰撞横梁等，而对全铝合金车身的关键技术研究微乎其微［6-8］。但随着国内电动汽车的飞速发展，对全铝车身结构设计的研究迫在眉睫。因此，为探究铝合金车身结构设计方法，本文中以铝合金下车体为例开展结构设计的关键技术研究。

与传统钢制车身相比，铝合金下车体的特点主要体现在：（1）结构布置的差异，一方面铝合金下车体要承载庞大的电池包质量，须在车体底部规划出整块电池包的安装空间，无法实现车身底部横梁和纵梁交错的结构布置，另一方面铝合金下车体的关键梁是等截面的铝型材结构，无法变截面意味着受到的空间约束更多；（2）结构连接上的差异，铝合金下车体采用型材、铸件和少量铝板相结合的技术，主要梁结构采用型材，不规则的且对性能影响较大的部位采用铸件，型材、铸件和板材相互之间采用MIG保护焊连接，而焊缝的连接强度只有母材的60%～70%左右［9］。基于上述要求，采用空间的拓扑优化、单根梁的拓扑优化和截面属性换算（以传统车关键梁截面的惯性矩作为铝合金下车体关键梁惯性矩的参考）、接头结构的经验评估和考虑挤压工艺的梁截面轻量化设计等方法，建立铝合金下车体结构的概念模型。

而在详细设计阶段，上述结构布置和连接上的特点同样成为关注的重点。一方面要解决铝合金车体的有限元仿真方法的问题，另一方面由于特殊的结构布置形式和连接方式，需要有合理有效的整体结构评估形式对此进行评估。而在国内外，尽管对铝合金车身的有限元仿真进行了大量的研究，但少有资料对铝合金车身有限元连接方法进行说明［10］。同时对于铝合金车身的整体评估方法的研究更是少之又少。因此，本文中以铝合金下车体为研究对象，探讨铝合金车身的有限元线性仿真分析方法，并基于广义结构刚度探究车身结构的整体评估方法。

1 铝合金车体的线性有限元仿真分析

1.1 铝合金下车体的有限元建模

下车体主要由铝合金型材和铝铸件焊接和螺栓连接而成，因此建立的有限元模型有以下特征：（1）型材采用面网格进行模拟，各个面之间共节点；（2）综合考虑计算的精度和效率，网格的基本尺寸采用5 mm；（3）铝型材之间的MIG保护焊采用shell单元进行模拟，具体模拟方式参考图1；（4）螺栓连接采用bolt单元模拟。由此得到铝合金车体有限元模型如图2所示。其中节点104 443个，壳单元个数共106 847个，三角形单元1 924个，三角形网格占比1.8%。

MIG保护焊的模拟参数为

式中t1和t2分别为两焊接面的厚度。两焊接材料中屈服强度较小者作为焊缝的材料。

1.2 铝合金下车体的性能仿真

参考钢制白车身下车体平台的性能控制策略［11］，将弯曲刚度、扭转刚度、1阶弯曲模态和1阶扭转模态作为铝合金下车体的控制指标。其中弯曲刚度描述的是汽车在满载情况下，在静止或平直路面上行驶时下车体抵抗变形的能力。扭转刚度描述的是汽车在坑洼路面上行驶时下车体抵抗变形的能力。模态分析的目的是通过识别车体在自由振动时的固有频率，达到对下车体基本NVH性能的控制，是车体设计开发阶段的重要环节。对铝合金下车体的上述基础性能进行控制时，可将成熟的、已平台化的下车体性能作为结构设计的参考指标，以保证下车体的刚度和振动要求，同时确保与上车体组合后白车身的性能要求。

下车体弯曲刚度的分析方法为：在下车体的前后悬架安装点各施加不同自由度的约束，在通过前后悬架安装点的X平面与门槛梁上平面的交点上各施加-Z向的1 000 N的力，如图2所示。

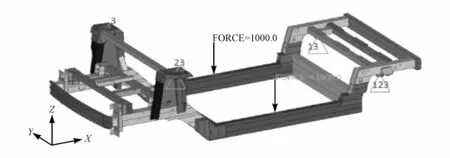
图2 车体有限元模型和弯曲刚度的边界条件

弯曲刚度的计算公式为

式中z1和z2分别为载荷作用点在门槛梁下底面上投影点的Z向位移的绝对值。

扭转刚度的分析方法为：分别在下车体的后悬架安装点约束不同的自由度，在前悬架安装点施加MPC约束，同时在一侧施加＋Z向的3 546.0 N的力，如图3所示。

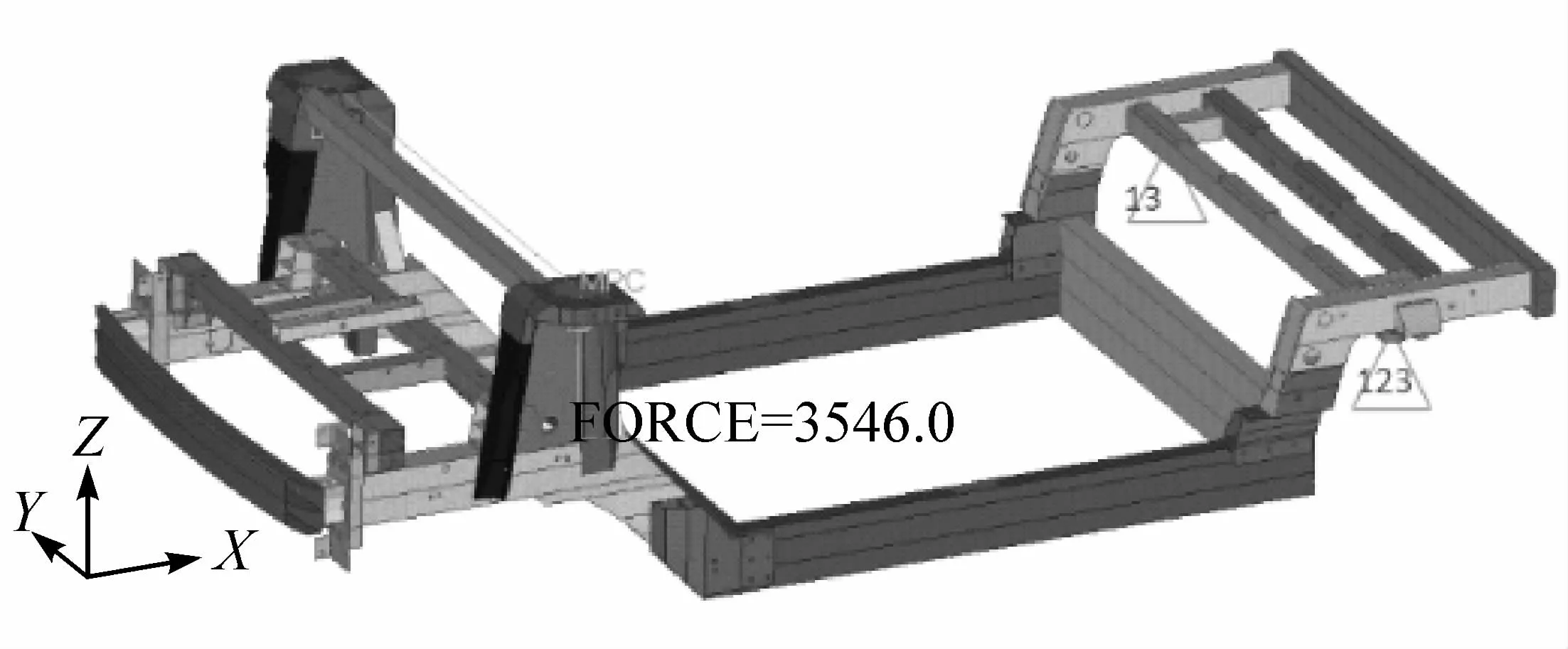
图3 车体的扭转刚度边界条件

扭转刚度的计算公式为

式中：z3和z4为前减振塔中心点在前纵梁下底面投影点（测点）的Z向位移绝对值；l为两测点间的距离。

模态分析时运用MSC.Nastran的SOL103进行求解（Lanczos法），分析时不添加任何约束，不考虑前6阶刚体模态（＜1 Hz），分析的频率范围为1～70 Hz。

仿真分析得到的各工况下的位移云图如图4～图7所示。

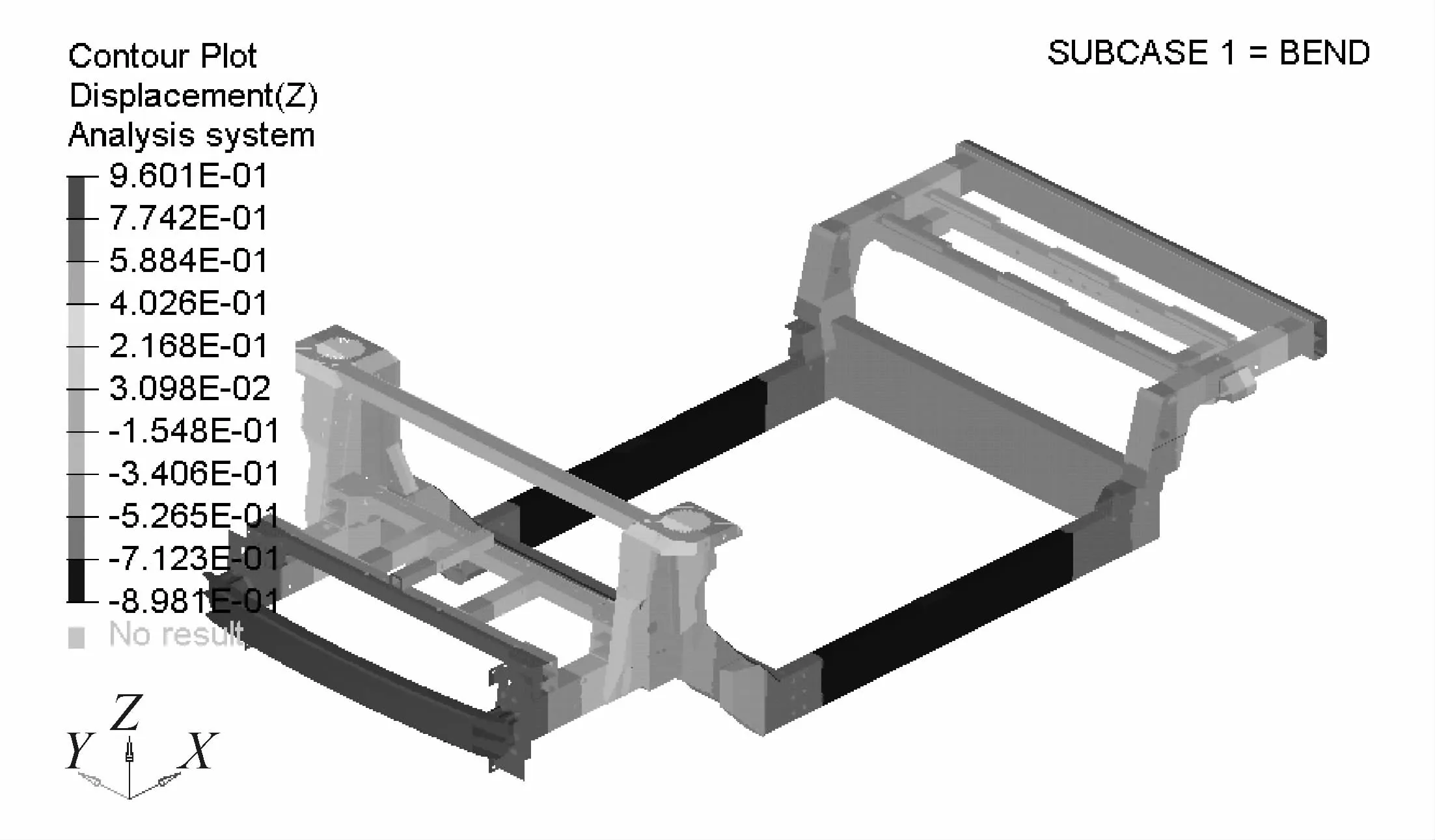
图4 车体的弯曲刚度位移云图

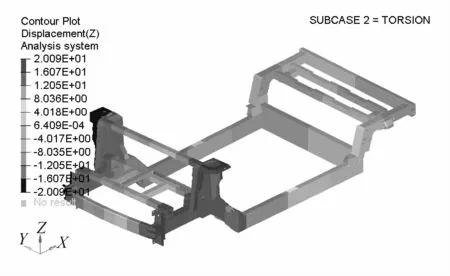
图5 车体的扭转刚度位移云图

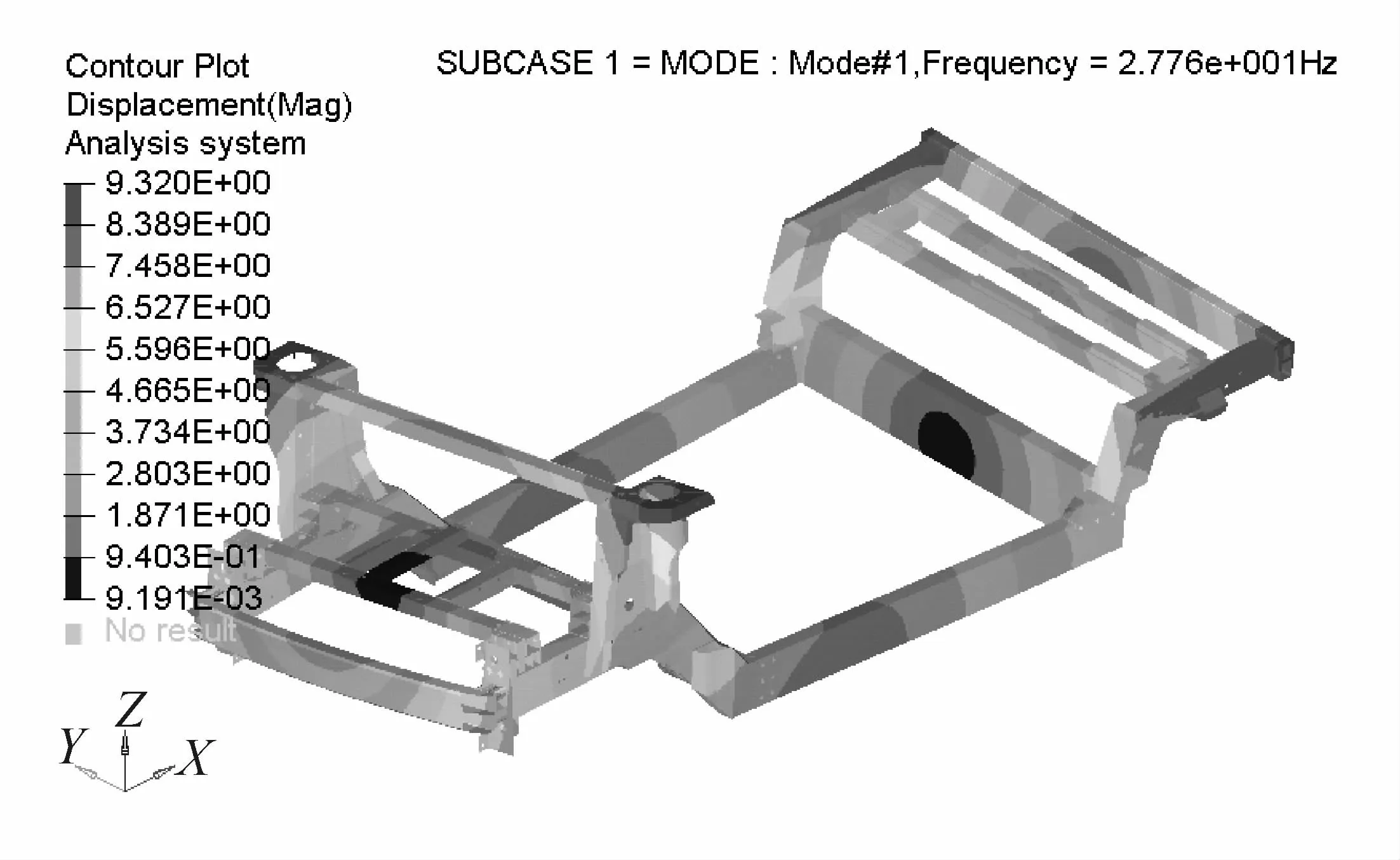
图6 车体的1阶扭转模态位移云图

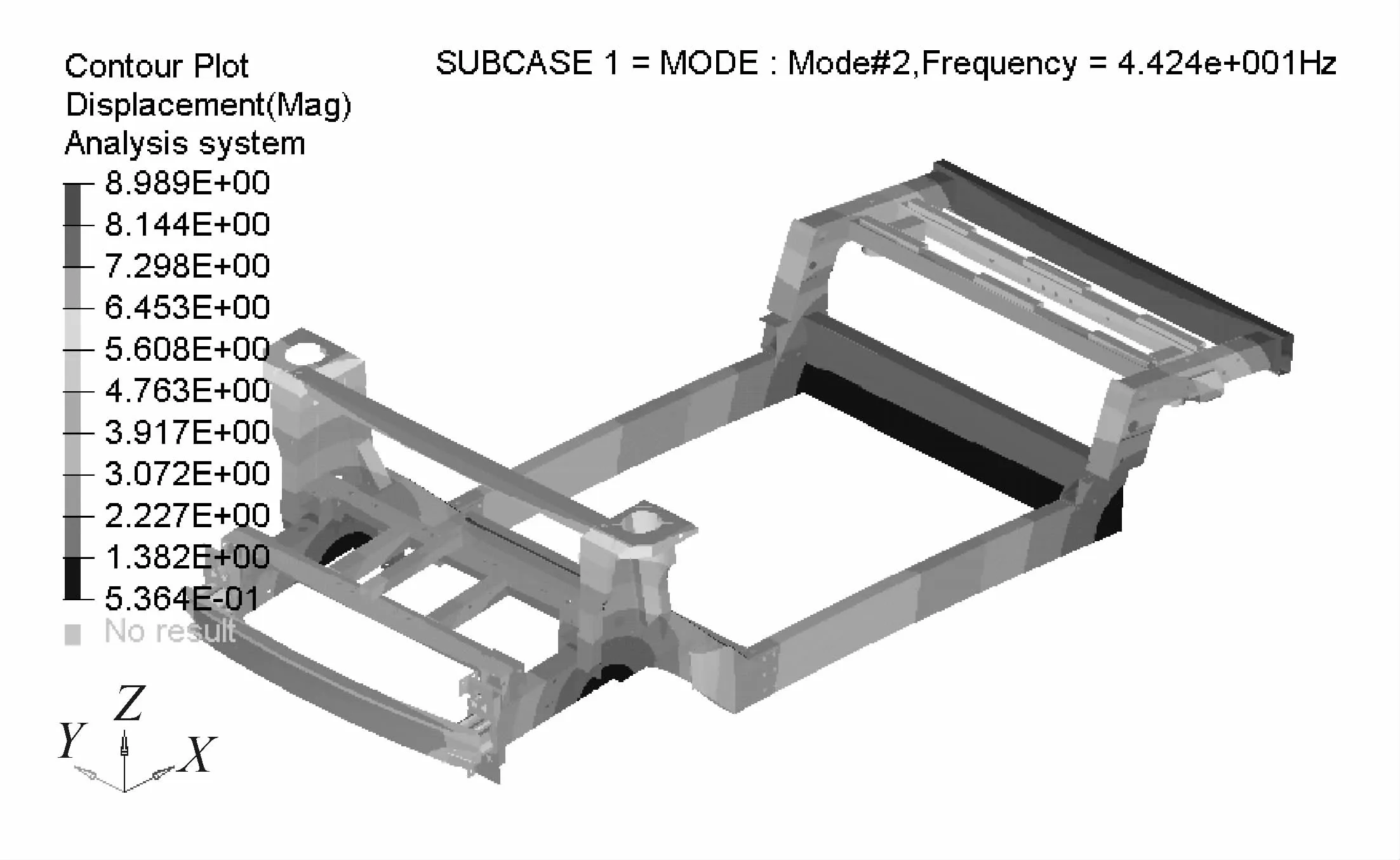
图7 车体的1阶弯曲模态位移云图

1.3 铝合金下车体的刚度实验验证

弯曲刚度实验时，将下车体放置于实验台架上，用夹具约束前后悬架的连接点，用刚性梁以集中载荷的形式作用在门槛梁上的前后悬架中垂面位置，左右对称各1 000 N的加载力。实验点和模拟分析测点相同，并用传感器读取测点位移。整体现场如图8所示。

图8 下车体的弯曲刚度实验

扭转刚度实验时，用夹具约束后悬架弹簧与车身连接处，在前悬架处通过千斤顶施加200 N·m的扭矩，并用传感器读取测点变形位移。测试现场如图9所示。

图9 下车体的扭转刚度实验

模态实验时将车体的前舱及行李舱处与橡胶绳连接，分别在右前悬架、左后悬架安装处施加激励，右前悬架处的激励向后倾斜45°，左后悬架弹簧处的激励垂直向上，这样有利于同时激励出横向、纵向及垂向模态，采用力学传感器采集激振力信号。同时在车体上均匀布置86个加速度传感器，采集车身模态变形的几何形状。车体的模态实验现场见图10。

图10 车体的模态实验

表1为铝合金下车体的性能仿真结果与实验值的对比。由表1可知，弯曲刚度和扭转刚度的误差分别为-2.45%和-3.59%，1阶扭转和弯曲模态的误差分别为-2.73%和-3.43%。仿真结果与实验结果基本吻合，误差绝对值均小于5%，表明铝合金下车体的有限元模型是正确的。

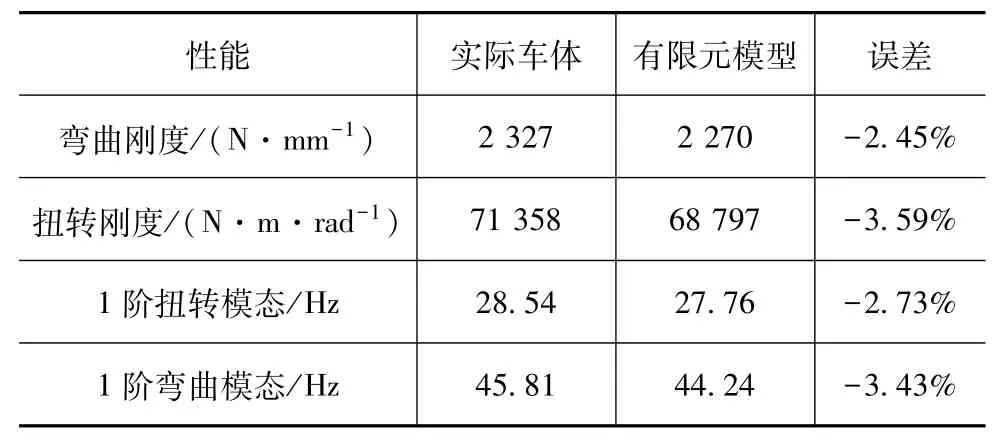
表1 弯曲和扭转工况下仿真与实验值的对比

2 广义结构刚度的理论基础、评价指标与计算方法

2.1 广义结构刚度的理论基础

广义结构刚度作为评价结构中的任意一点与载荷的施加点之间的刚度连接关系的一种物理量，能解释载荷在车体中的传递路径并对结构的内部刚度进行评估。基于广义结构刚度的车体载荷传递路径识别方法是一种在不同边界条件下基于结构内部应变能的数值评估方法。

如图11（a）所示，点A是结构的受力点，点B是支撑点（约束点），点C是结构内部的任意点，式（5）代表了A，B和C 3点之间的相互关系。

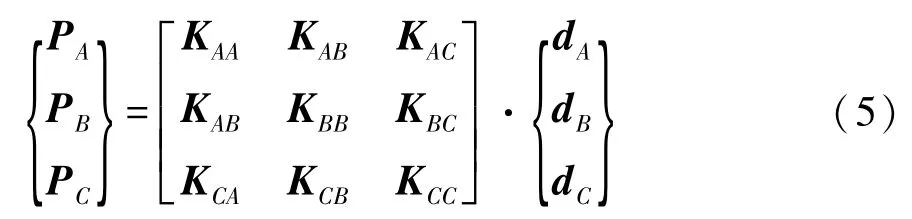
式中：Pi（i=A，B，C）表示结构在i点受到的外力向量；Kij（i，j=A，B，C）表示i点与j点间的刚度矩阵；di（i=A，B，C）表示i点的位移。结构的整体应变能U表示为

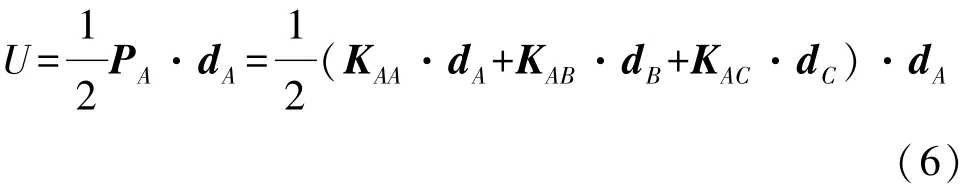
由于点B是约束点，所以dB=0，因此

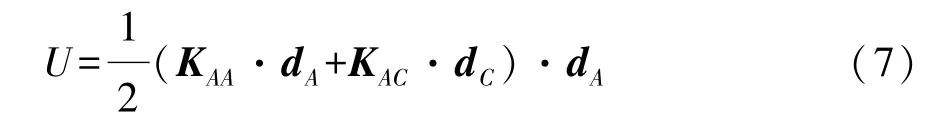
如果同时把点B和任意点C约束，在A点施加强制位移dA得到A点的支反力P′A，见图11（c）。此时dB=0，dC=0，结构约束条件的改变引起刚度矩阵的改变，式（5）可写为

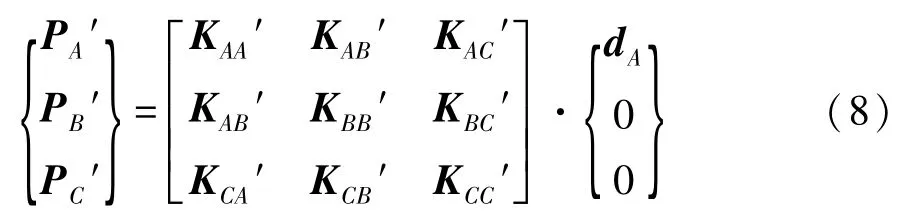
则结构的应变能U′表示为

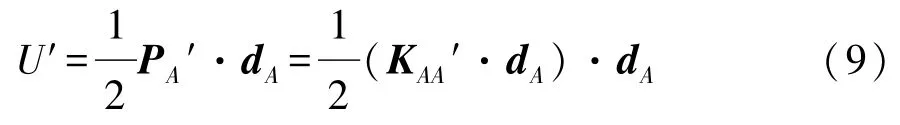
广义结构刚度的定义为

图11 广义结构刚度说明示意图

基于式（10）即可求得每个点处的广义结构刚度。由于广义结构刚度是结构内部刚度大小的表征，因此，广义结构刚度值较高的部位即是结构中的主要传力部位。借用梯度函数表示结构的传力路径，定义λ为U*沿着A至B方向上的梯度函数，则

因此，从A点至B点，梯度最小点连成的曲线就是主要的传力路径，如图12所示。

2.2 广义结构刚度的评估标准

（1）均匀性评价指标 均匀性评价指标描述的是传力路径上各点U*值的变化趋势。图13（a）中定义l为结构的载荷作用点到结构约束点之间的传力曲线的总长度，定义s为传力路径上的点到载荷作用点之间的距离，定义s／l为横坐标、U*为纵坐标的曲线表征均匀性评价指标曲线。图13（a）中虚线为理想的传力路径曲线，是一条斜率为负的直线。基于理想的均匀性曲线，给出均匀性评价指标：结构的实际均匀性曲线（图中实线所示）偏离虚线的程度（方差），偏离程度越小表征结构的传力效果越好。

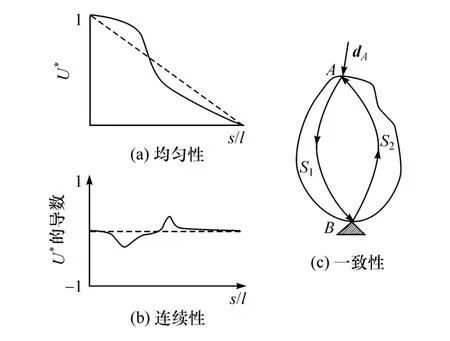
图13 广义结构刚度的评估指标

（2）连续性评价指标 连续性评价指标是对图13（a）中曲线的求导。描述的是从施力点到约束点之间U*递减的均匀性。图13（b）中虚线所示U*相对于s／l的斜率为定值，是理想的受力结构形式。图中实线表示实际的受力结构的连续性曲线，实线的上下波动的幅度越小或越贴近虚线表明结构的受力效果越好。通常用虚线与实线围成的面积作为评价结构性能好坏的参数之一。

（3）一致性评价指标 均匀性与连续性评价指标表示从结构的载荷作用点到结构约束点之间的传递效果的好坏，一致性评价指标描述的是：作用在结构上A点的载荷通过结构内部的传力路径S1传到约束点B和以B点作为载荷输入点，以A点作为约束点，载荷通过结构内部的传力路径S2从点B传到点A时，S1与S2的差异性。对于理想的结构路径S1与S2是吻合的，所以一致性就是对S1和S2之间差异性大小的描述，如图13（c）所示。当S1和S2越靠近时，表征结构的传力效果越好。

基于以上评估结构传力性能好坏的3个指标，合理的结构设计应该是载荷在结构之间的传递是连续的、突变较小的，同时载荷的传递路径一致性良好。

2.3 广义结构刚度的计算方法研究

由式（10）可知，为得到结构中任意点处的U*值，需要计算结构的整体应变能U和任意点约束时结构的应变能U′。因此每计算一个点的应变能U′，结构的边界条件就要改变一次，计算的次数就等于模型节点个数。如果采用手动修改边界条件求解U*值的方法，计算工作量将会非常庞大。本文中借助MSC.Nastran和Isight两大成熟商用软件，运用实验设计（DOE）的思想，将节点ID号作为实验设计变量的水平，从而将重复的对边界条件的修改视为DOE实验设计的过程，实现对节点广义结构刚度值的计算，简单易行。具体的计算流程如图14所示。

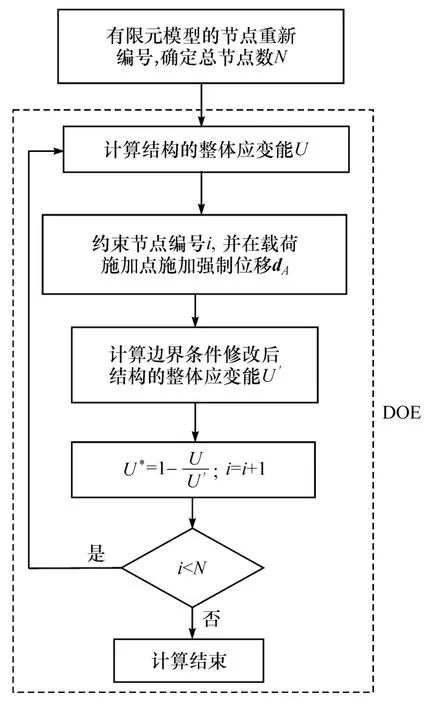
图14 广义结构刚度的计算流程

3 基于广义结构刚度的铝合金车体整体结构评估与改进

3.1 基于广义结构刚度的车体传力性能评估

以车体左前悬架安装点至左后悬架安装点的载荷传递路径为例，对采用广义结构刚度识别传力路径的方法进行探究。如图15所示，约束后悬架安装点、右前悬架安装点的1～6自由度，在左前悬架安装点处施加Z向载荷P=1000 N，作为结构的初始边界条件。

图15 车体传力路径计算的初始边界条件

基于图14的计算流程对车体的传力路径进行计算，图16为整个车体的U*分布云图，基于最小梯度绘出从左前悬架受力点到左后悬架的主要传力路径（图中实线所示）。同时，运用均匀性和连续性评价指标对车体的传力路径进行评估，结果如图17和图18所示。

由图16可知，基于广义结构刚度的传力路径识别方法能清晰地描绘出载荷从受力点至约束点之间的主要传递路线。由于是计算每个节点的广义结构刚度，故细小的结构单元如焊点、螺栓等在载荷传递中的作用都能显现。

图16 车体的广义结构刚度分布云图

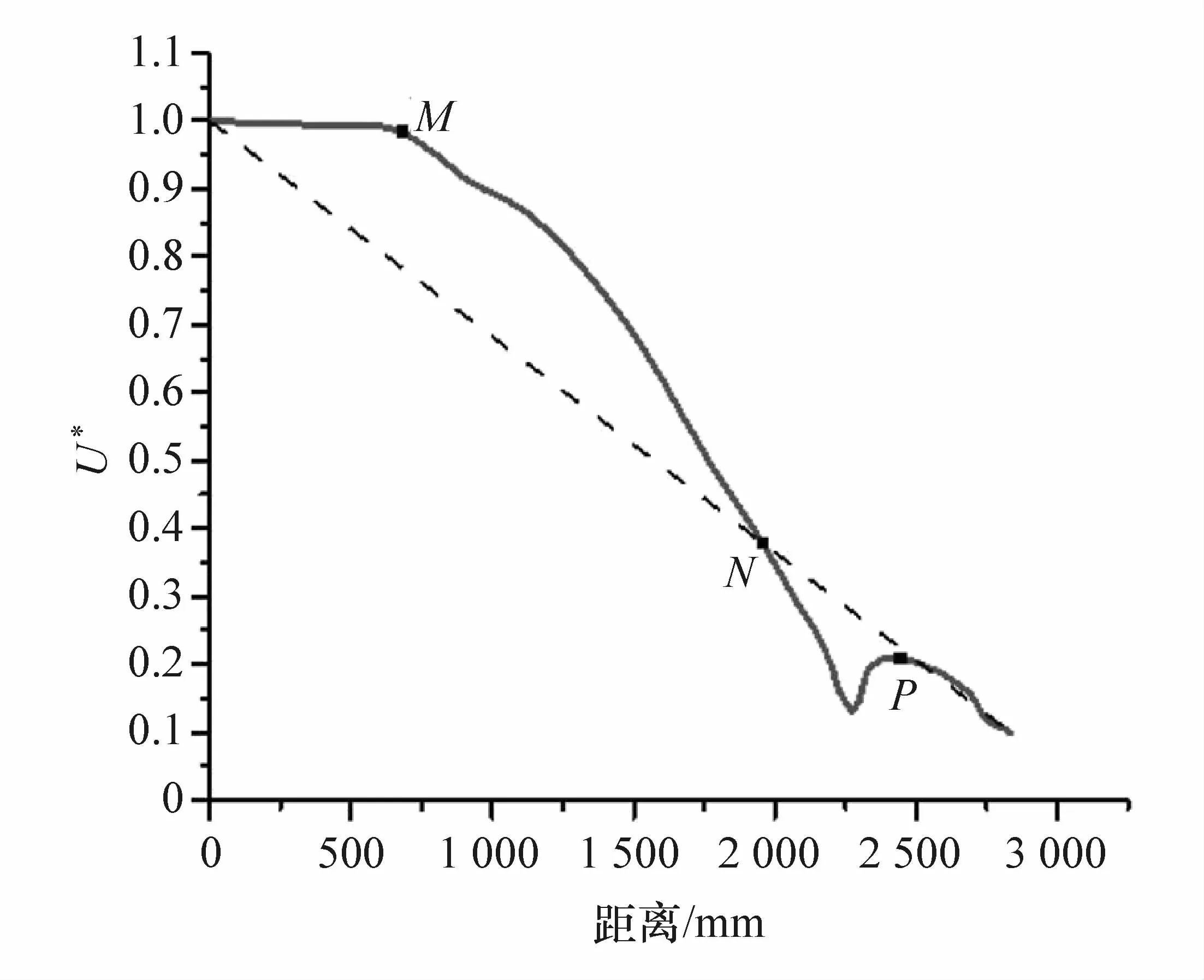
图17 车体传力路径的均匀性评估曲线

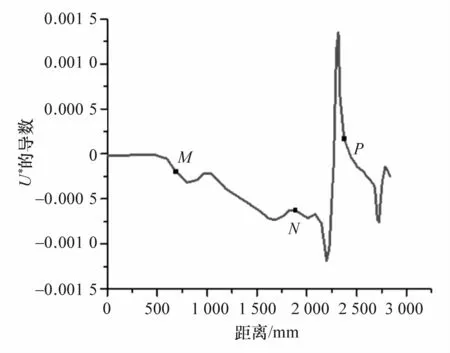
图18 车体传力路径的连续性评估曲线

由图17和图18可知，载荷从前悬架安装支架至前舱边梁的过程中出现拐点，M点之前广义结构刚度值变化较小，M点之后广义结构刚度值迅速降低。结合局部放大云图（图19）可知，作用于前悬架安装点上的主要载荷先经过前悬架支架加强筋传至A点，从A点沿着前悬架支撑型材内表面至B点，从B点传至前舱边梁E点的过程中由于型材中空导致C点至E点的传递路线中断（图19中的虚线），从而载荷沿图中的A→B→D→M→E路线至前舱边梁。由此造成M点之前结构的相对刚度较高，M→E的过程中结构薄弱，广义结构刚度值迅速降低。

此外，由图17和图18可知，从N点至P点之间的门槛梁后接头U*的均匀性、连续性较差。主要表现为N→P之间U*的连续性出现先减小再增加的极小点，导致连续性评价指标的NP段出现大于0的极大值，且方差较大。N，F，G，P点对应的门槛梁后接头的位置如图20所示。

3.2 车体结构的改进与性能验证

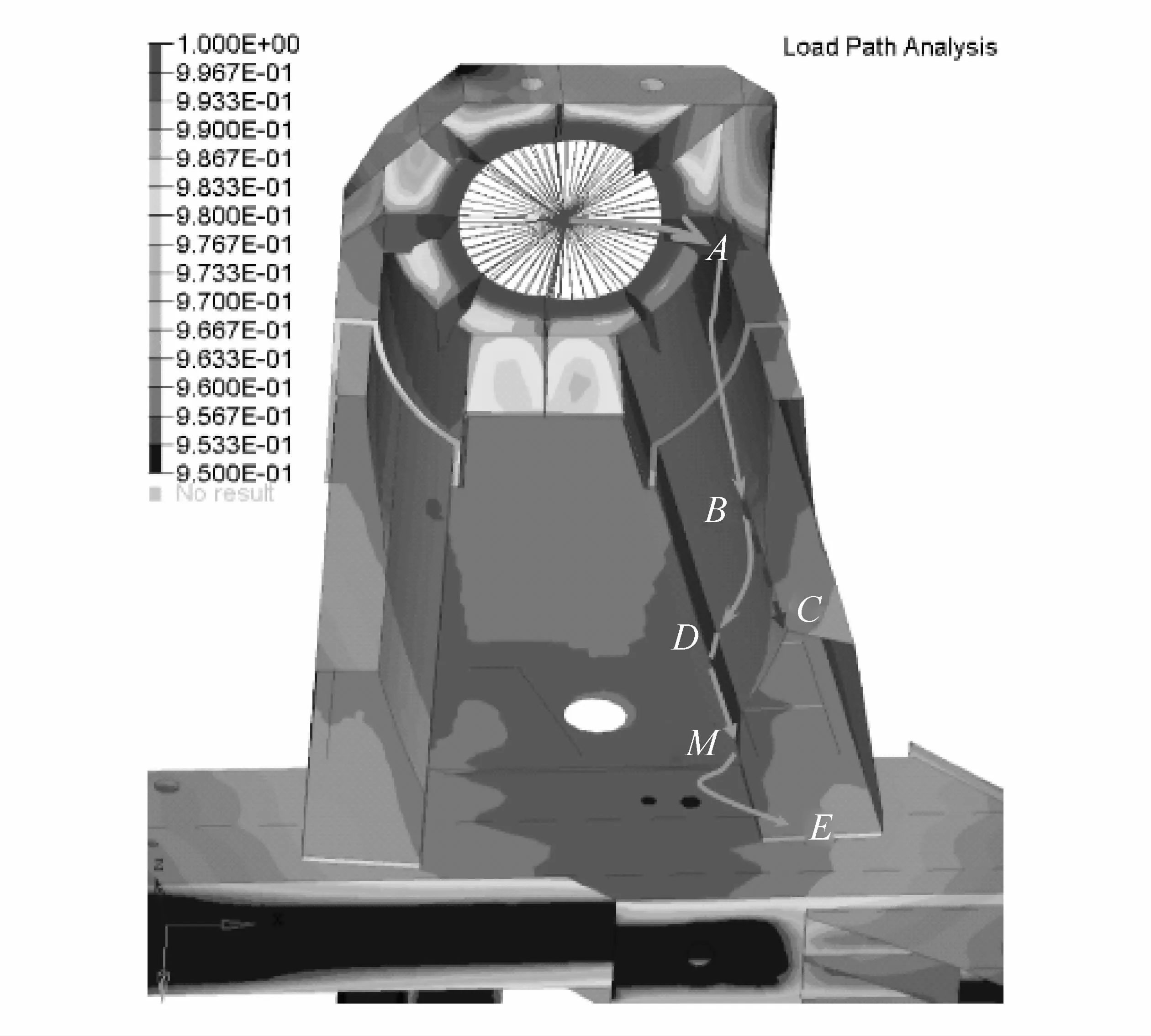
图19 车体前悬架至前舱边梁的传力路径

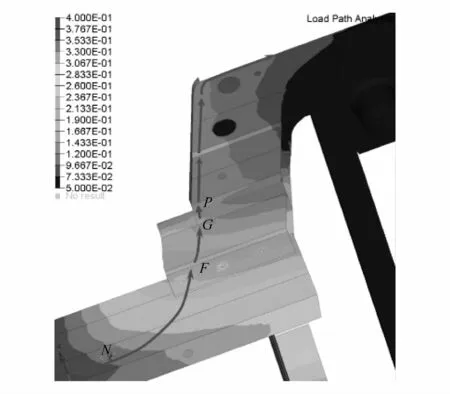
图20 车体门槛梁至后悬架的传力路径

综上对车体有限元模型的传力路径分析可知，车体的结构设计有两处存在一定缺陷，一是前悬架支撑型材与前舱边梁的搭接结构，二是门槛梁的后接头结构，且由连续性指标可知，后者对车体的性能影响更大。本节中以门槛梁的后接头结构为例，进行结构改进，并将改进前后的刚度特性进行对比，以证明基于广义结构刚度的传力路径识别方法的正确性。

为分析门槛梁后接头结构的设计缺陷，截取车体门槛梁后接头的局部结构视图，见图21。由图20和图21可知，作用于车体内部的载荷在N→G作为平面内部力进行传递，而在G点时，FG平面的内部载荷转化为垂直作用于PG所在平面的平面外部载荷。此变化是引起车体局部刚度下降的主要原因。因此，采用如图22所示的方案进行接头结构的改进。具体描述为：在接头结构内增加加强面，如图22中K平面所示，加强面厚度选用与FG平面等厚度的2.0 mm。同时为使载荷的传递更加平顺，去除门槛梁与接头搭接时宽度差（参考图20，F点的宽度差）的影响。

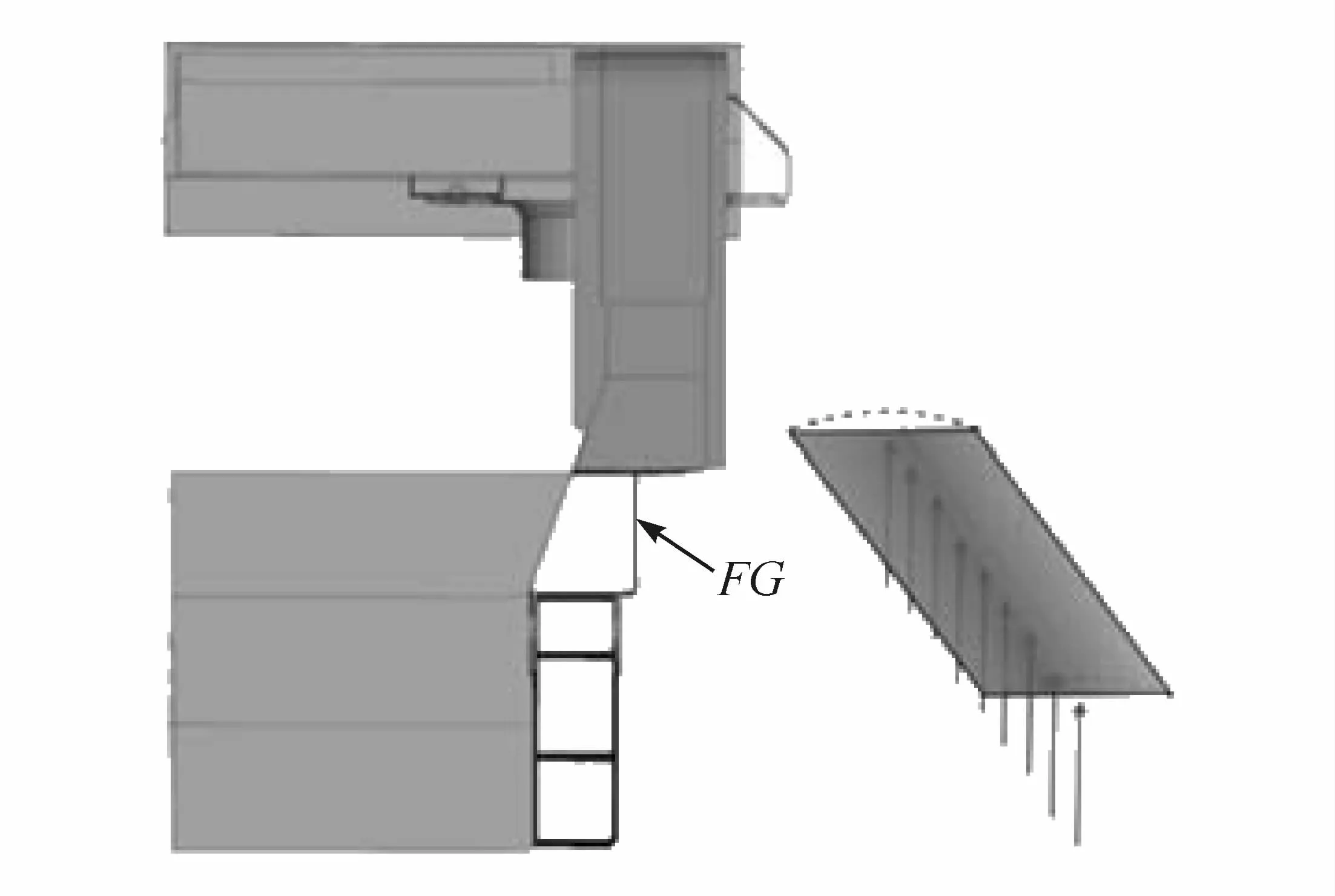
图21 门槛梁后接头改进前结构

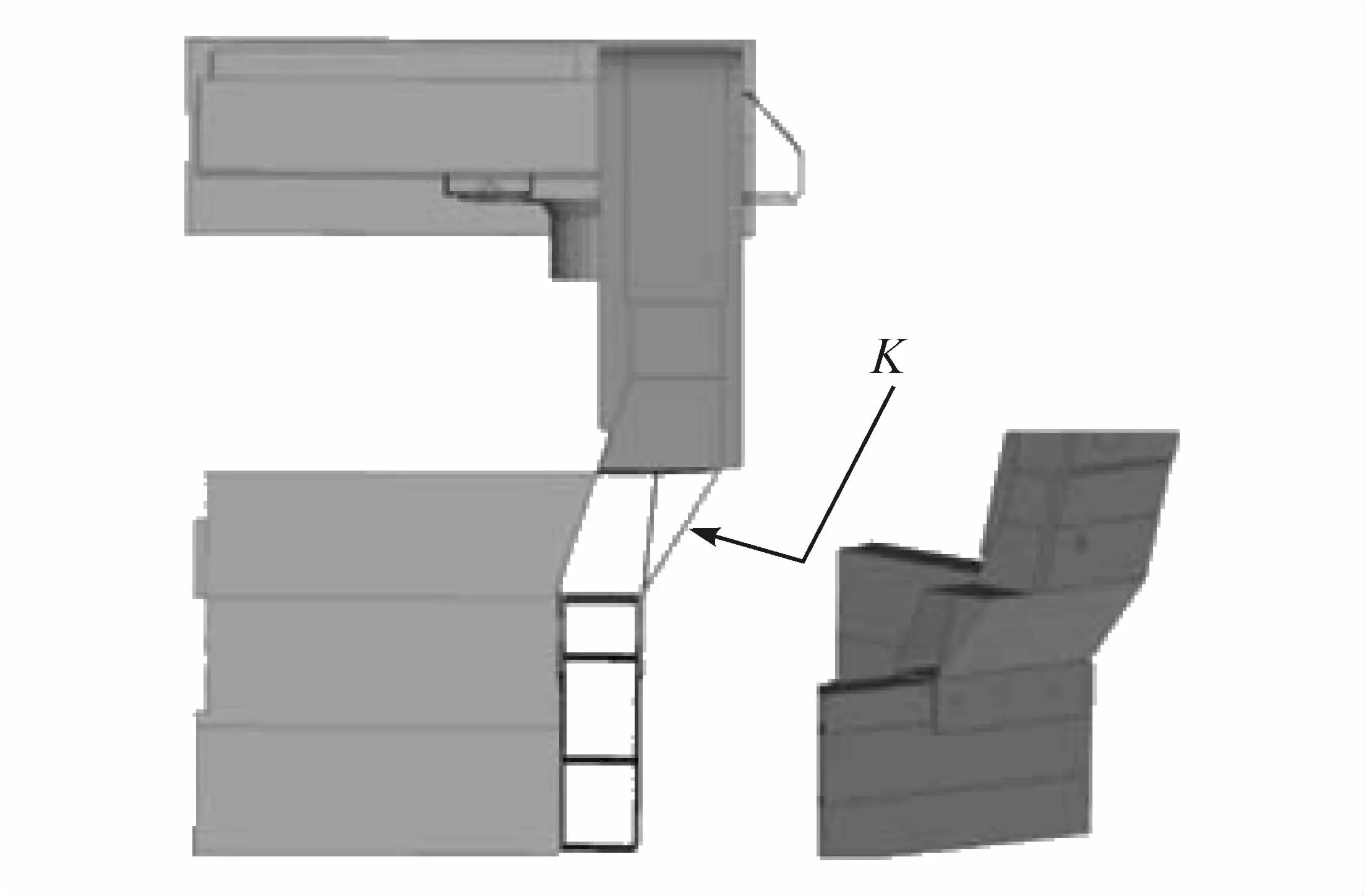
图22 门槛梁后接头改进后结构

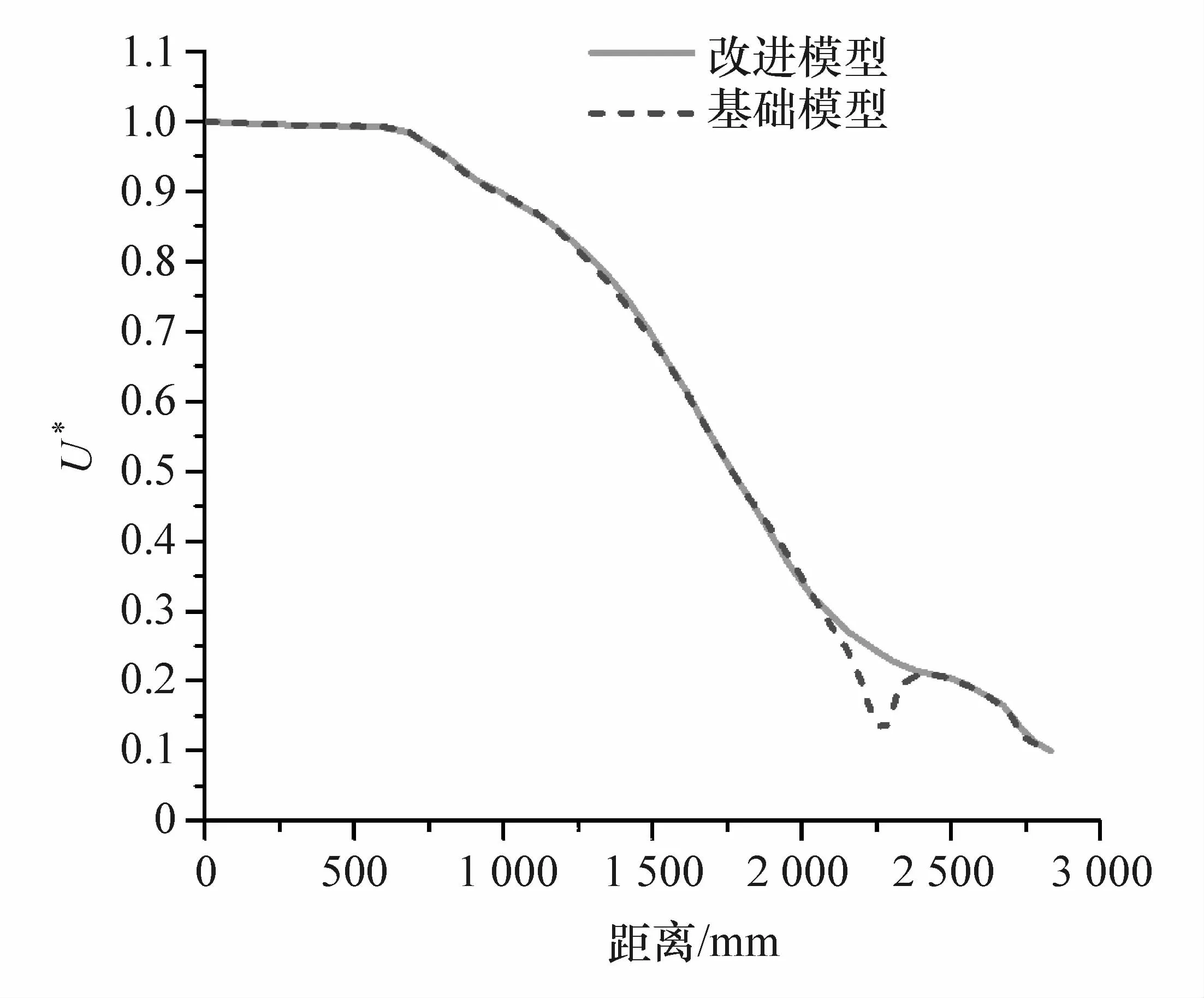
图23 接头改进前后车体传力路径的均匀性评估曲线对比

采用均匀性指标和连续性指标对改进前后车体的整体传力路径曲线进行对比评估，如图23和图24所示。由图23可知，改进后车体传力路径的均匀性曲线的整体趋势与改进前保持一致，在门槛梁后接头处有效避免了极小值的出现，U*值在此处呈现梯度性降低的趋势，均匀性有很大的改善。由图24可知，车体接头结构改进后连续性曲线的波动区间由［-1.18E-3，1.35E-3］减小为［-7.5788E-4，-8.6446E-6］，波动幅度明显降低，车体传力路径的连续性有较大提高。

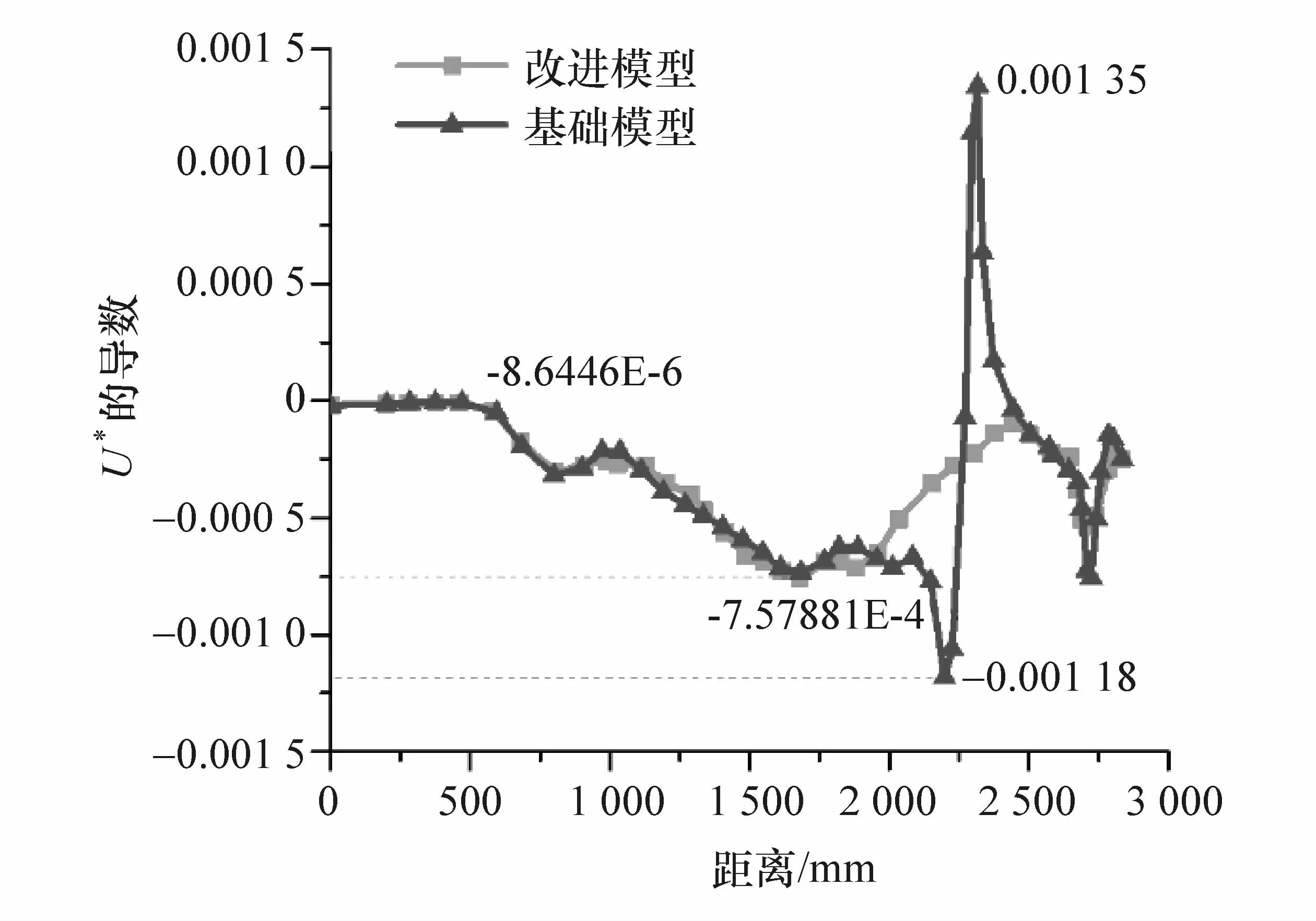
图24 接头改进前后车体传力路径的连续性评估曲线对比

为验证车体门槛梁后接头改进后车体性能的提升效果，基于图22的改进结构计算车体的刚度特性，并与改进前的结构对比，详细对比结果见表2。

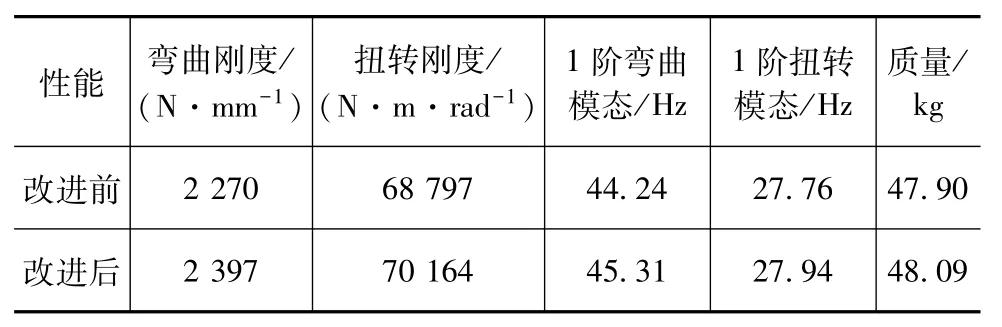
表2 门槛梁后接头改进前后车体的刚度特性对比

由表2可知，改进后在质量稍有增加（0.19 kg）的情况下，车体的弯曲刚度、扭转刚度、1阶弯曲模态和1阶扭转模态分别提升了5.59%，1.99%，2.42%和0.65%，效果明显。因此，直接验证了传力路径的均匀性和连续性评价指标的有效性，验证了基于广义结构刚度的传力路径分析方法在车体结构评估上的可行性。

4 结论

（1）采用shell单元模拟铝合金焊缝，并开展车体的刚度、模态性能的有限元仿真与实验对比，仿真误差均小于5%，证明了仿真方法的正确性。

（2）提出将广义结构刚度运用于铝合金车体的结构评估中。运用DOE实验设计思想避免了每个点广义结构刚度的重复计算。基于广义结构刚度的最小梯度原则识别出车身左前悬架和左后悬架中设计的薄弱区域，并对其进行改进，改进后在质量稍有增加（0.19 kg）的情况下，车体的弯曲刚度、扭转刚度、1阶弯曲模态和1阶扭转模态分别提升了5.59%，1.99%，2.42%和0.65%，效果明显，验证了基于广义结构刚度在结构整体评估中的有效性。