自主学习干扰观测器驱动的重复使用运载器再入段滑模控制

陈佳晔，穆荣军，白瑜亮，张 新，崔乃刚

(哈尔滨工业大学航天工程系，哈尔滨 150001)

0 引 言

近年来，由于重复使用运载器(Reusable launch vehicle, RLV)具有降低发射成本、全球快速可达、飞行安全可靠等优势，在航空航天、军用民用等领域内成为研究热点。由于RLV的再入段具有速度变化范围大、模型不确定性显著、外部环境存在严重干扰以及多通道存在较强耦合等特点，使得RLV再入段控制系统设计面临更大挑战[1-2]。因此，设计对飞行环境、外界干扰以及模型不确定性都具有鲁棒性的先进控制器对于提升RLV再入段飞行控制性能具有重要意义。

近期众多学者对再入飞行器控制系统设计方法进行了研究，如增益调度[3]、轨迹线性化方法[4]、动态逆[5]、状态Riccati方程[6]、反演控制[7]等。尽管这些线性和非线性控制方法能够跟踪再入段RLV的制导指令，但滑模控制方法在考虑到模型不确定性和外部干扰时，则更为有效[8]。为更好地解决RLV再入段存在干扰无法建模的问题，根据其特点设计相应的干扰观测器，以提高系统的鲁棒性。在文献[8]中，设计了一种基于干扰观测器的非线性动态逆控制方法，控制导弹纵向自动驾驶，相关研究中的主要问题是：基础非线性干扰观测器(Basic nonlinear disturbance observer，BNDO)只能估计时不变干扰，如果干扰随时间变化，BNDO对干扰的估计值将存在偏差。目前，虽然有众多非线性观测器可供使用，例如扩展卡尔曼滤波器、粒子滤波器以及非线性序贯+迭代时域估计方法等，但粒子滤波器和滚动时域估计方法的计算量较大，需要的计算时间较长[11]。因此，设计一种计算简单、能够估计时变干扰的观测器的需求非常迫切。

本文针对RLV再入飞行阶段的复杂特性，根据奇异摄动理论及时标分离原则将RLV动力学方程分解为内、外环子系统，由于在该飞行阶段存在模型不确定性和未建模的外部时变干扰，设计基于2型模糊神经系统结构的SLDO，用于观测和估计干扰，与传统的干扰观测器相比，该方法具有更强的鲁棒性和更高的计算效率，且可在未知干扰边界时对干扰进行有效估计。通过仿真校验，基于SLDO设计的RLV多元超螺旋滑模控制器，可准确地实现再入段姿态跟踪，并快速收敛。

1 RLV动力学模型

RLV的刚体6自由度动力学方程是由3自由度平动方程以及3自由度转动方程组成。

3自由度平动方程如下所示：

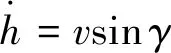
(1)

(2)

(3)

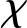
(4)

(5)

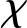
(6)

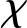
3自由度转动方程表示为：

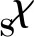
(7)

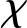
(8)

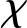
(9)

(10)

(11)

(12)

式中：α为攻角，β为侧滑角，σ为倾侧角，ωx,ωy,ωz分别表示滚转角、偏航角以及俯仰角角速度，Jij(i,j=x,y,z)为飞行器的惯量，Mx,My,Mz分别表示滚转、偏航和俯仰力矩。

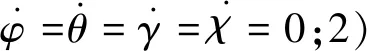
(13)

(14)

(15)

为了尽可能准确地描述RLV再入飞行段过程，需要考虑由于简化模型和不同通道之间的耦合带来的模型不确定性。因此，一个更加实际的面向控制的动力学模型如下：

(16)

(17)

y=Θ

(18)

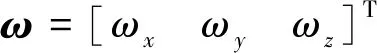
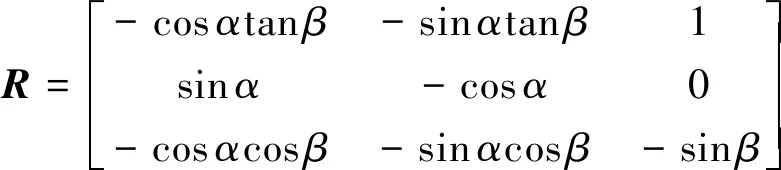
控制力矩矢量M如下所示：

(19)

式中：Cl,Cm,Cn是空气动力学力矩系数，通过三次多项式拟合方法，将它们随α∈[-10°, 40°],Ma∈[0.4,7]的变化拟合为：

Cl=0.02-0.05Ma-1.2×10-3α+0.02Ma2-

7×10-4Maα+1×10-4α2-1.7×10-3Ma3+

1.5×10-4Ma2α-1.8×10-5Maα2-

4.42×10-7α3

Cm=0.45-0.24Ma-6×10-3α+0.05Ma2+

1.7×10-3Maα+3.32×10-5α2-2.9×

10-3Ma3-1.4×10-4Ma2α+1.37×10-6

Maα2+1.5×10-7α3

Cn=-8×10-4-0.05Ma-5×10-3α+

0.014Ma2-0.008Maα+3×10-4α2-

0.005Ma3+0.005Ma2α-1×10-3Maα2-

3×10-5α3

为了方便后文设计，将上述由式(16)～式(18)描述的姿态控制动力学模型写为下列形式：

(20)

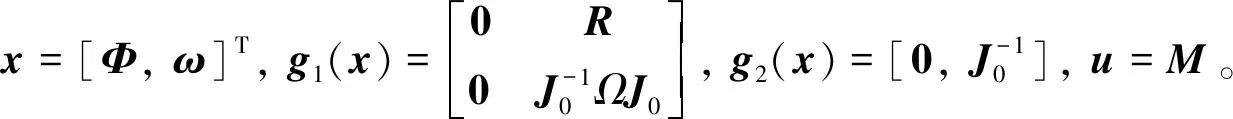
2 基于自学习干扰观测器的滑模控制器

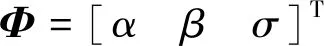
2.1 自主学习干扰观测器设计

2.1.1基本非线性干扰观测器

在第1节建立的面向控制系统动力学模型(20)中，干扰d(t)在实际情况下是不可测量的，需要对其进行估计，从而提高控制系统的鲁棒性。文献[9]中提出的BNDO如下所示：

(21)

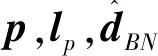
(22)

(23)

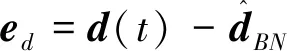
2.1.2基于T2NFS的自学习干扰观测器

本文所设计的自学习干扰观测器形式如下：

(24)

式中：τc，τr和τn分别代表传统估计律项、鲁棒估计律项和T2NFS项。图2为自学习干扰观测器的结构图。

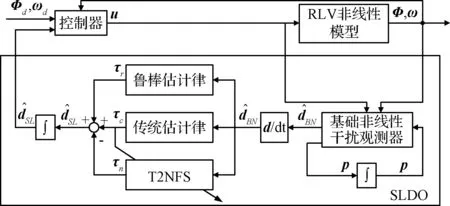
图2 自学习干扰观测器(SLDO)示意图Fig.2 Framework of the self-learning disturbance observer(SLDO)

传统估计律项定义如下：

(25)

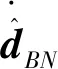
鲁棒估计律项形式如下：

(26)

lrZ为正，即lrZ>0,lr代表鲁棒增益向量。

1)2型神经模糊结构

区间2型TSK(Takagi-Sugeno-Kang)的if-then模糊规则Rij定义如下：

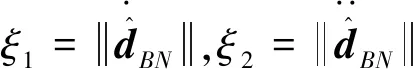
按照A2-C0模糊系统规则，激活值计算方法如下所示：

(27)

网络输出公式如下所示：

(28)

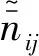
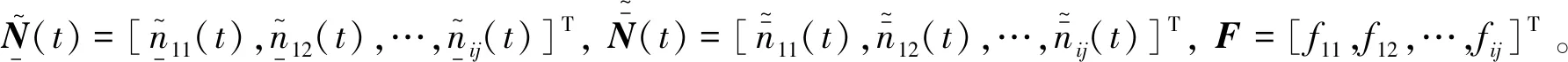
2)基于滑模控制理论的学习算法

将滑模面设计为如下形式：

s(τc)=τc

(29)

式中：τc为传统估计律输出值，采用滑模面作为学习误差来训练基于滑模控制理论的学习算法，过程如下所述。

T2NFS参数的适应规则：

(30)

(31)

ηsgn(s)

(32)

(33)

(34)

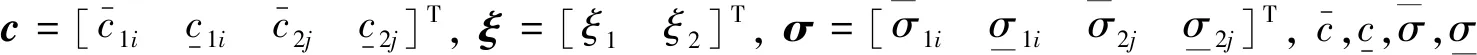
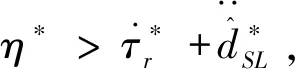
证.李雅普诺夫函数写为如下形式：

(35)

根据文献[10]可得：

(36)

(37)

由上述设计可以看出，在2型神经模糊结构中采用基于滑模控制理论的学习算法具有自适应能力，因此SLDO能够在未知干扰的上界以及干扰对时间的一阶导数的上界时对干扰进行估计。

2.2 基于SLDO的多元超螺旋滑模控制器

根据奇异摄动理论及时标分离的原则，系统中的角速度与姿态信息变化快慢不同，将控制系统分为快慢回路，使控制系统能够在存在模型不确定性以及外部干扰时，跟踪指令姿态角Φd以及期望角速度ωd。

2.2.1外环控制器设计

对于子系统(16)，设计实际控制ωd使得姿态角Φ能够在考虑模型不确定性Δf的情况下，在有限时间内跟踪制导指令Φd。

定义跟踪误差为：

eΦ=Φ-Φd=[eΦ1,eΦ2,eΦ3]T

(38)

eΦ的导数为：

(39)

为了使系统以较快的速度收敛到平衡点，设计新型滑模面如下：

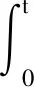
(40)

其中，γΦ1≥1,0<γΦ2<1,kΦ>0。

对式(40)求导可得：

(41)

设计基于多元超螺旋算法的快速到达控制律如下所示：

(42)

然后，将式(42)代入式(41)，设计连续虚拟控制律为：

(43)

2.2.2内环控制器设计

设计控制力矩M使ω能够在考虑到模型不确定性ΔJ和外部干扰Δd时，跟踪上期望指令ωd。

根据方程(17)，可得如下方程：

(44)

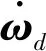
内环多变量SLDO被设计为方程(48)和(51)。

(45)

辅助滑模变量如下：

sM=eω-wM

(46)

方程(46)对时间的导数为：

(47)

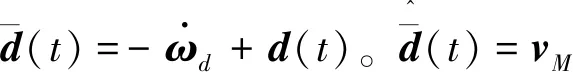
(48)

将式(48)代入式(47)可得：

(49)

采用类似外环控制器的设计方法设计内环系统控制器，定义快速滑模面：

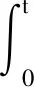
(50)

式中：kω>0，常数γω1≥1,0<γω2<1。

应用与式(42)相似的控制律可得：

(51)

2.2.3稳定性证明

(52)

对于系统(52)，定义如下李雅普诺夫候选函数：

(53)

根据文献[11]中类似的证明过程，若取

可得：

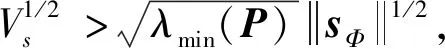
可以得到结论：如果参数kΦ1,…,kΦ4都选择合适，sΦ以及其导数能够内收敛到零。

(54)

考虑到如下正定李雅普诺夫函数：

(55)

其导数可以被写为：

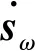
3 仿真校验

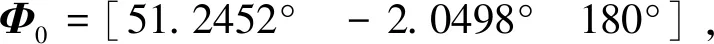
针对系统(16)～(18)，设置不确定性参数为ΔI=random(0,1)×10%I0，其中I0(kg·m2)为RLV再入段转动惯量常数矩阵，其形式为I0=diag(56241,1×106,985392) kg·m2，外部时变干扰d(t)×105(N·m)，其中

分别采用BNDO和SLDO两种观测器对干扰进行观测，得出两种观测器估计值以及干扰估计误差，如图3所示。从图3可以看出，对于阶跃类常值的干扰，SLDO与BNDO对干扰的估计速度相近，都能够比较快地估计出干扰值并且收敛至真值附近；对于随时间变化的干扰值，SLDO的收敛速度比BNDO快，收敛效果也比BNDO好。仿真结果说明,SLDO可以有效地估计时变干扰，收敛速度和收敛效果都优于BNDO。

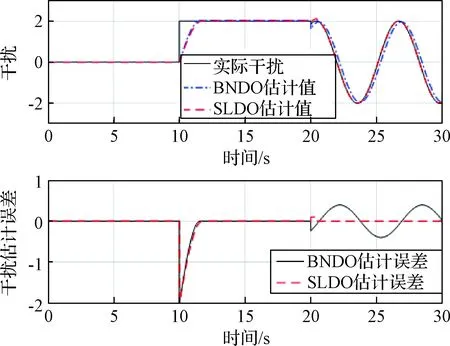
图3 BNDO或SLDO对干扰观测值Fig.3 Curves of estimation value from BNDO and SLDO

针对RLV再入段对控制系统进行仿真校验，首先选取PID控制方法与本文所提出的控制方法进行对比分析，仿真结果如图4～图5所示。

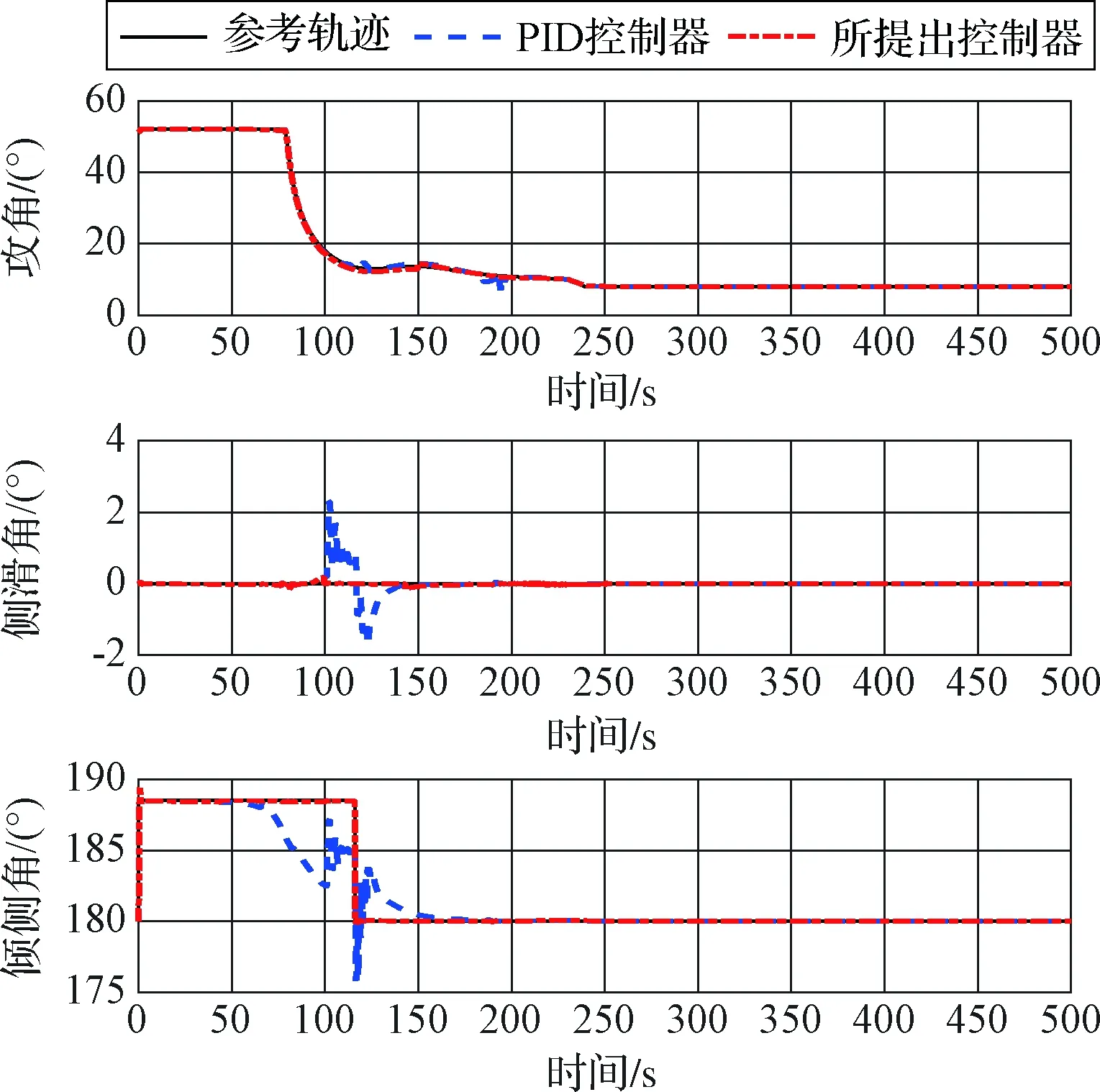
图4 PID控制系统以及所提出控制方法的跟踪曲线Fig.4 Tracking curves of the PID control system and the proposed control system

图4中曲线分别为PID控制系统以及本文所提出控制系统的攻角、侧滑角以及倾侧角跟踪轨迹曲线，图5为两种控制方法输出的误差曲线。

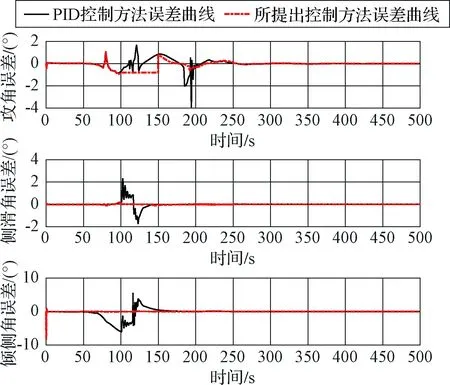
图5 PID控制系统以及所提出控制方法的姿态跟踪误差Fig.5 Tracking error of the PID control system and the proposed control system

从图4～5可以看出，本文所提出控制系统对三个角的最大误差分别为1.05°，0.2°，1°以内，而PID控制系统的三个角最大误差分别为3.89°，2.3°，6.1° 以内，本文所提出的控制器在系统存在不确定性时的跟踪误差小于传统PID控制器的跟踪误差，收敛速度快、收敛效果好。

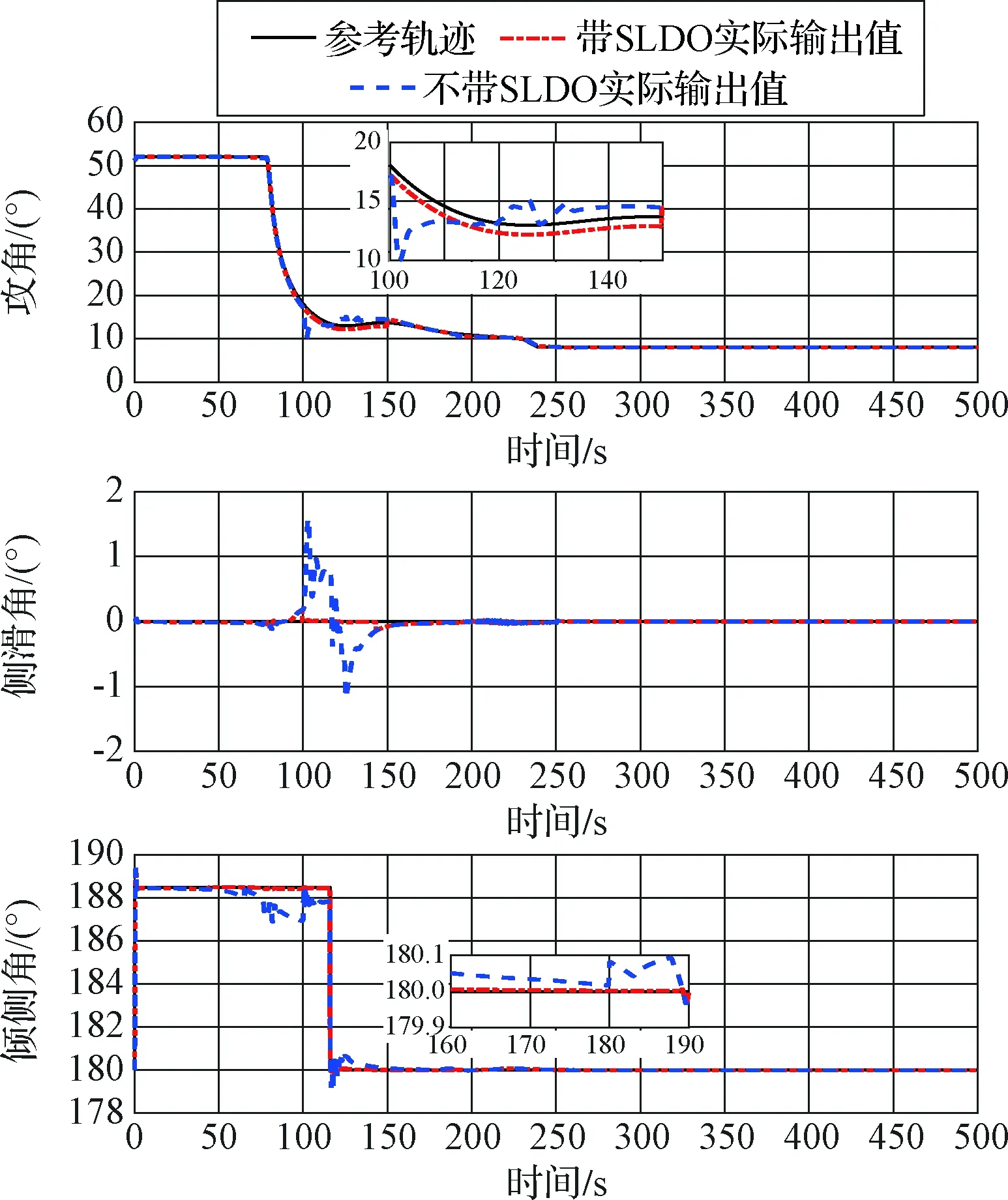
图6 有无SLDO的控制系统输出曲线Fig.6 Curves of the outputs from control system with and without SLDO

其后，选取有无SLDO的控制系统进行仿真对比分析，图6分别为有无SLDO情况下的控制系统输出的姿态角Φ曲线，通过仿真结果可以看出，在存在未知时变干扰时，基于SLDO的控制系统与不含有SLDO的控制系统相比，精度更高、抖动更小、收敛速度更快、控制效果较好、满足控制需求。

4 结 论

本文针对RLV再入段存在时变不确定干扰情况下的控制问题进行了研究。提出了自主学习干扰观测器，该观测器结合了基础非线性干扰观测器、传统估计律、鲁棒估计律以及T2NFS项，实现了在未知干扰边界情况下对时变干扰的观测和估计，并分析和证明了观测器学习算法的稳定性。然后提出了由SLDO驱动的多元超螺旋滑模控制方法，根据干扰估计值调整控制器的参数，从而使控制器更具鲁棒性，实现对姿态指令的跟踪。以某型RLV再入段为研究对象，进行数值仿真，通过BNDO和SLDO的干扰观测对比，校验了SLDO对时变干扰的估计能力优于BNDO；通过PID控制系统与SLDO驱动的控制系统对比，校验了在系统中存在时变干扰时，SLDO驱动的控制系统的收敛更快、收敛效果更好；通过对有无SLDO情况下的控制系统输出对比，校验了由SLDO驱动的多元超螺旋控制方法能够有效估计外部干扰和模型不确定性，提高控制精度。