利用增量相位和星光仰角增强XNAV

焦 荣，甘 伟，肖志红，崔占琴

(西安石油大学电子工程学院，西安 710065)

0 引 言

卫星实现自主导航是未来发展方向。X射线脉冲星导航(X-ray pulsar navigation，XNAV)具有自主性好、适应性强、能输出全导航参数等优势受到广泛关注。XNAV测量脉冲星信号到达航天器和选定惯性参考点之间的时间差来获取航天器的位置信息，类似全球定位系统(Global positioning system, GPS)，因此也被称为“自然界的全球定位系统”[1-2]。XNAV的主要问题是精度还不理想，常采用差分来消除或减小误差，如脉冲星相对定位法。文献[3-5]分别提出基于相位差测量的相对导航递推算法；另一类重要的方法是采用多源融合，如文献[6-7]提出使用太阳或行星等天体信息辅助X射线脉冲星提高定轨精度的改进方法；文献[8]设计出X射线脉冲星与惯性系统的组合方案，可有效降低航天器钟差和加速度计偏差；文献[9]把XNAV与多普勒测速导航相结合，采用多普勒差分测速提高导航定位精度；文献[10]提出“脉冲星+光学”的组合导航方式。前期研究中曾将相位增量信息融合加权最小二乘方法，有效提高卫星初轨定轨精度[11]。相位增量指在两个时刻信号从脉冲星到达航天器的相位差，因为抵消了部分共性误差，可以提高估计精度。考虑到传统天文导航具有观测方便，信号采样周期短的优势，本文将恒星星光仰角信息引入XNAV降低脉冲星导航误差积累，提高滤波器收敛速度。X射线脉冲星导航系统是典型的非线性系统，常用的非线性滤波方法如扩展卡尔曼滤波器、无迹卡尔曼滤波器(Unscented Kalman filter, UKF)对于过程噪声的不当假设也导致滤波估计性能不佳[7]。文献[12]将自适应差分卡尔曼滤波器(Adaptive divided difference filter , ADDF)应用到火星探测器导航中，表明ADDF具有良好的噪声适应能力，能有效提高导航精度。鉴于以上原因，本文提出用ADDF融合脉冲星计时观测、相位增量及恒星星光仰角等信息的增强XNAV方法，通过适应过程噪声协方差来估计系统的参数和状态，提高导航精度。

1 多信息测量模型

1.1 计时观测模型

脉冲星距离太阳系可达几万光年，因此在太阳系脉冲星辐射方向可近似认为常矢量。脉冲星信号具有稳定的周期，其到达太阳系质心(Solar system barycenter, SSB)的相位可用模型来预测。如果已知参考时间原点t0时刻的初相φ(t0)，脉冲频率f及其多阶导数，在SSB处t时刻的相位φ(t)可用相位演化模型精确预测[13]：

(1)

同时信号由航天器到SSB的传输时间td可表示为

(2)

XNAV的观测模型可表示为光行时和噪声之和：

Y1=g1(X,t)+v1=td+v1

(3)

式中：td为不同时刻脉冲星信号从航天器到达SSB的时间延迟;v1为脉冲星测量噪声，它是均值为零的高斯白噪声，其方差由脉冲星测量精度决定[1]。

1.2 相位增量模型

使用脉冲星相位增量信息可以提高传统XNAV精度。当探测器连续观测同一颗脉冲星时，相邻两个时刻的相位差受相对论影响较小，所以相位增量在理论上具有更高的测量精度。相位增量模型如图1所示。

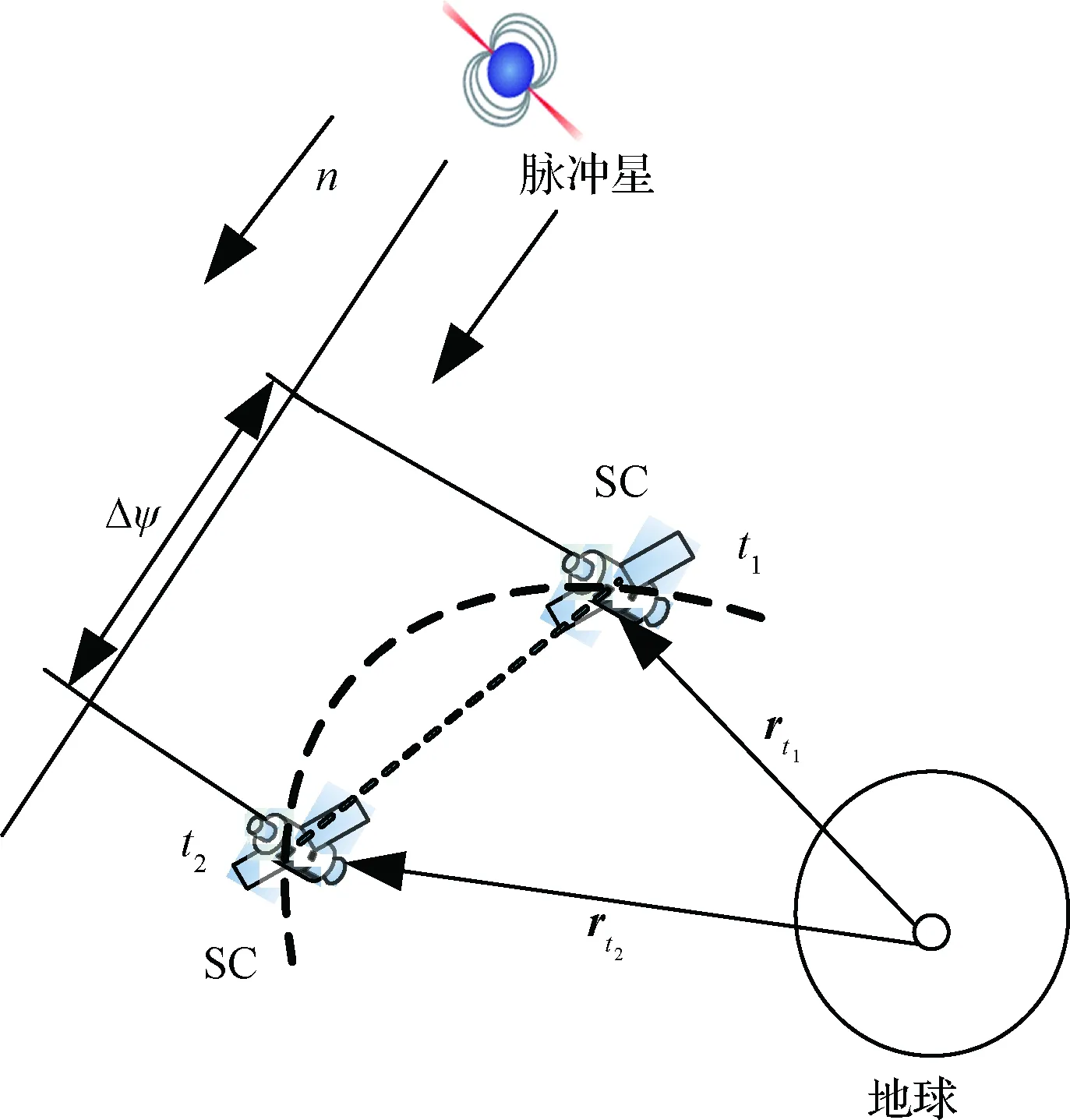
图1 相位增量观测的几何模型Fig.1 Geometric model of incremental phase observation

图1中，t1和t2分别表示卫星轨道的两个时刻，其相位差可以表示为

Δψ=ψt2-ψt1

(4)

式中：ψt1和ψt2分别表示t1和t2时刻脉冲星和卫星之间的相位；rt1和rt2为卫星相对于地球中心在t1和t2时刻的位置矢量。

用位置矢量rt1和rt2推导Δψ表示为

(n·δr)-(|rt1|+|rt2|)|δr|+2(n·b)(n·δr)-

(5)

式中：δr=rt2-rt1。

在太阳质心参考系中，b=|b|约为106km量级，D0为1014km量级。假设到达时(Time of arrival, TOA)的观测时间为500 s，航天器速度为10 km/s，δr为102km量级，(|rt1|+|rt2|)|δr|/D0,(n·b)(n·δr)/D0均为10-7km量级，可忽略不计。式(5)可重写为

Δψ=Δt/P=n·(rt2-rt1)/cP

(6)

相位增量观测模型可写为：

Y2=g2(X,t)+v2=Δψ+v2

(7)

式中：v2为零均值的高斯白噪声，其方差由脉冲星测相精度决定。

1.3 星光仰角观测模型

星光角距和星光仰角是天文导航最常用的观测量。与星光角距相比，星光仰角在低轨道或者传感器视场较窄时，可观性更好，定位精度更高[14]。本文将星光仰角作为观测量，其几何模型如图2所示：

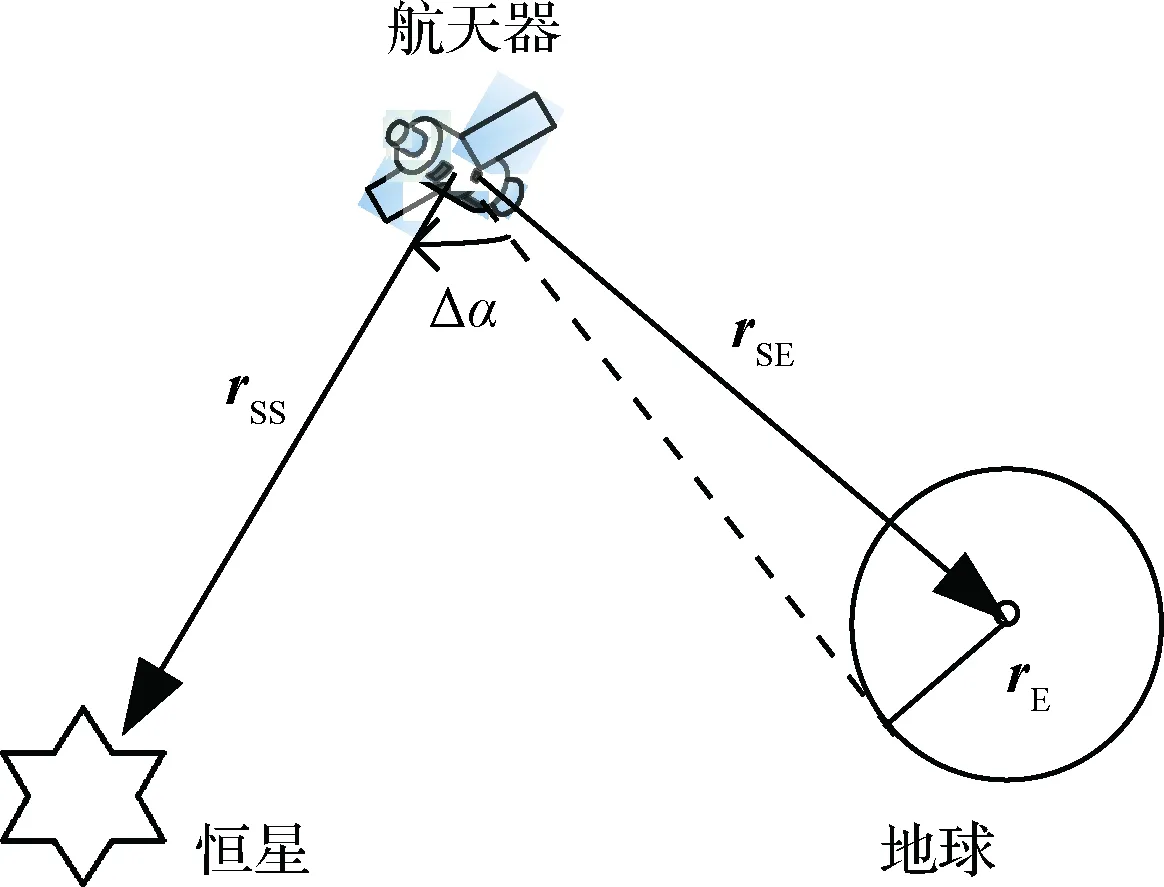
图2 星光仰角的几何模型Fig.2 Geometric model of star elevation

星光仰角是指利用星敏感器观测到的导航恒星与地球边缘的切线方向之间的夹角，图2所示Δα即为星光仰角，由几何关系可知：

(8)

式中：rSS为导航恒星星光方向的单位矢量；rSE为航天器相对于地球的位置矢量；rSE=|rSE|为航天器和地球之间的距离，rE为地球半径。

因此，可得到星光仰角的测量模型为

Y3=g3(X,t)+v3=Δα+v3

(9)

式中：v3为零均值高斯白噪声，其方差由星敏感器精度决定。

2 自适应差分滤波融合方法

2.1 航天器轨道动力学模型

将航天器当成质点，在J2000.0 地心惯性坐标系中，航天器的轨道动力学模型可表示为

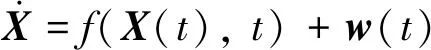
(10)

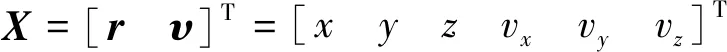
航天器状态模型[15]可进一步表示为

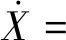
(11)

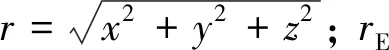
在已知初始状态的情况下，对式(11)积分即可得到航天器在任意时刻的运动模型。

2.2 ADDF滤波器

ADDF滤波器是一种迭代滤波算法，它将测量值协方差与理论值协方差间的差值作为调节噪声统计特征的自适应因子，能够有效抑制滤波器发散从而提高滤波精度[16-17]。

由第1节分析可知多信息融合后的测量方程为：

Y=[Y1Y2Y3]T=[tdΔψΔα]T+V

(12)

ADDF滤波结构如图3所示。

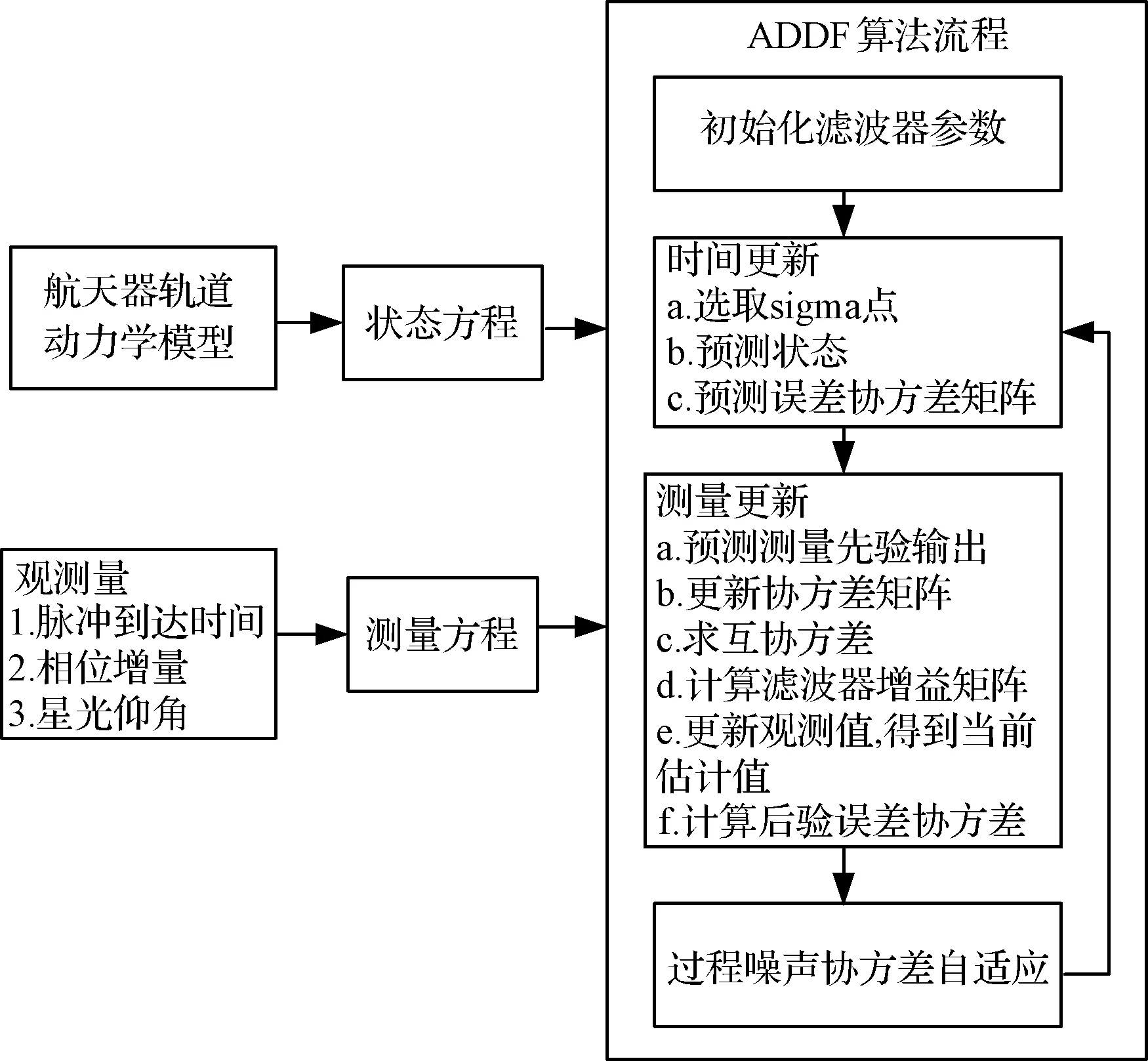
图3 ADDF滤波结构图Fig.3 Structure diagram of ADDF filter

3 仿真结果与分析

3.1 初始条件

仿真主要校验了脉冲星计时观测、相位增量及恒星星光仰角等多信息ADDF滤波器融合导航性能，并与UKF对比。仿真采用100次蒙特卡洛实验。

导航脉冲星选自XNAVSC数据库，它们分别为B0531+21、B1821-24、B1937+21。X射线脉冲探测器的探测面积为1 m2，背景噪声约为0.445 ph·cm-2·s-1。这组导航脉冲星的性能及参数详见文献[18]。

实验选择恒星HR-539、两颗现役导航卫星GPS_BII-04及ALOUETTE_1进行分析，在地心J2000.0惯性系中，各轨道参数如表1所示。

如果位置方差要求小于500 m，则脉冲星观测时间设置为300 s[18]，滤波400次。增强XNAV滤波器的仿真参数设置如下：

航天器初始状态误差为

δX(0)=

(13)

表1 仿真所用卫星轨道参数Table 1 Satellite orbit parameters for simulation

初始状态协方差矩阵为

P=diag((2km)2, (2km)2, (2km)2, (10m/s)2,

(10m/s)2, (10m/s)2)

(14)

初始噪声协方差矩阵为

Q=diag((20m)2, (20m)2, (20m)2, (1m/s)2,

(1m/s)2, (1m/s)2)

(15)

包括3颗脉冲星、相位增量和恒星星光仰角的观测噪声协方差矩阵可以表示为：

R=diag((0.109km)2, (0.325km)2,

(0.344km)2, (0.003rad)2, (0.003rad)2,

(0.003rad)2, (0.002rad)2)

(16)

3.2 仿真结果及分析

首先验证不同观测量增强XNAV的有效性。GPS_BII-04轨道下，不同观测下导航误差累积情况如图4所示。

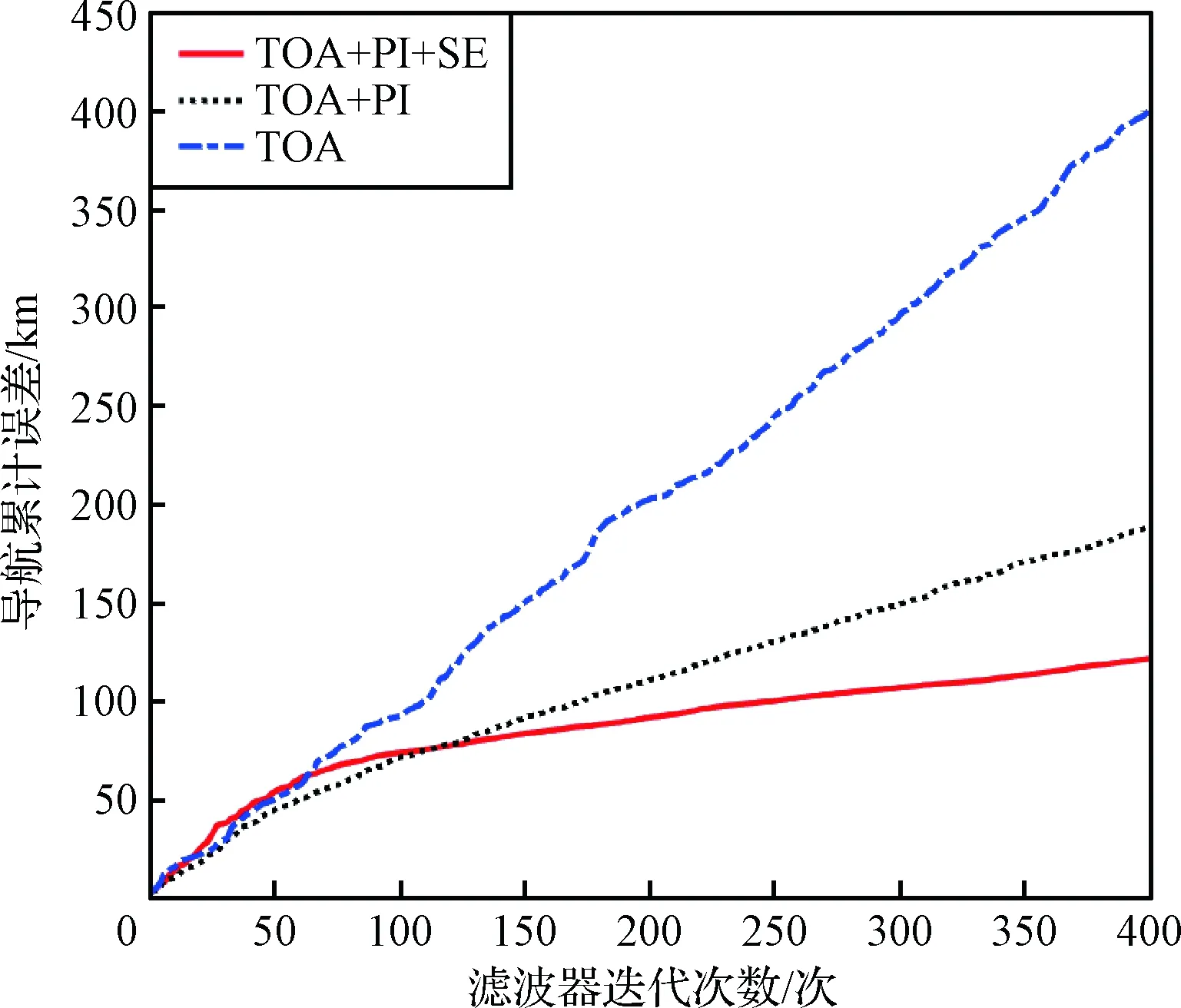
图4 融合不同观测量情况下系统累积误差曲线Fig.4 Cumulative error curves with different observations

图4中TOA表示计时观测，PI表示相位增量，SE表示恒星星光仰角。从图4可以看出，脉冲星计时观测系统的累积误差最大，滤波器收敛最慢；同时融合脉冲星相位增量信息及恒星星光仰角后，系统累积误差最小，收敛最快；融合相位增量和计时观测的系统介于两者之间。

不同观测量对系统导航精度的影响仿真结果如图5及表2所示。

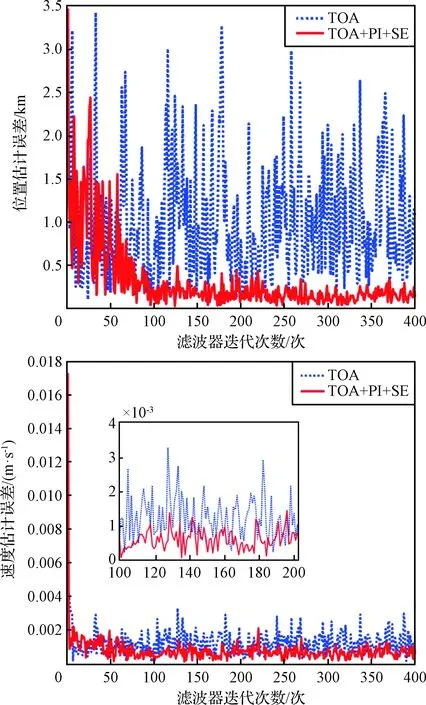
图5 不同观测量下的导航精度曲线Fig.5 Navigation precision with different observations

从图5可以看出，在相同的初始误差条件下，多信息融合XNAV算法比计时观测算法收敛速度快、状态估计误差明显降低。与位置估计误差相比，速度估计误差的改善程度要小，这是因为探测器初始速度较小且变化缓慢。在前70次的迭代中，ADDF位置估计性能并不是最好。这是因为ADDF滤波器自适应过程需要迭代20次才能完成，仿真中滤波器滑动窗口的大小设置为50，所以第70次迭代时才是滤波器正常工作的开始时间，取数也应该在这之后。

从表2可以看出融合相位增量信息能将位置估计精度提高50%左右，速度估计精度提高25%以上；同时融合相位增量和星光仰角，位置估计精度提高70%以上，达到200 m以下的位置估计精度，速度估计精度提高40%以上。

为验证ADDF在非线性系统状态参数估计中具有的优势，现将ADDF和UKF两种滤波器作对比分析。在GPS_BII-04轨道下，ADDF和UKF滤波仿真图如图6所示。

表2 GPS_BII-04卫星状态估计值Table 2 State estimation value of GPS_BII-04

注：TOA-计时观测，PI-相位增量，SE-星光仰角

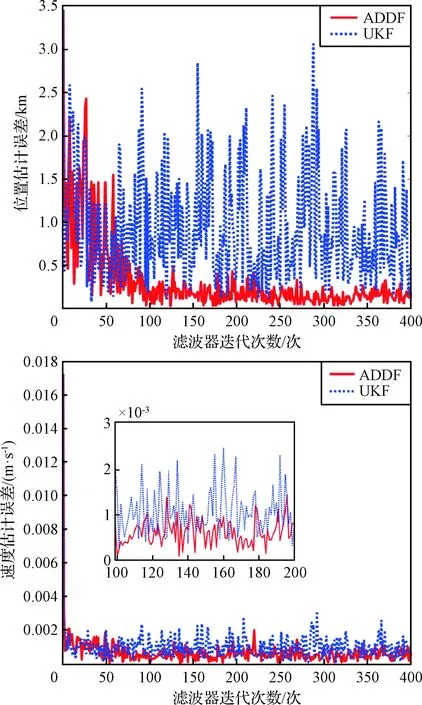
图6 不同滤波器估计误差曲线Fig.6 Navigation precision with ADDF and UKF

从图6位置估计误差曲线可以看出：在前70次迭代中，UKF和ADDF估计性能相差不大；70次迭代之后，ADDF通过实时调节过程噪声估计的协方差矩阵，使得滤波算法收敛更快、估计精度更高，而UKF采用固定不变的过程噪声协方差矩阵，与ADDF相比，UKF估计的位置和速度误差更大。

为了验证所提方法对不同导航卫星的适用性，采用相同方法对卫星ALOUETTE_1进行轨道滤波。其仿真结果如表3所示。

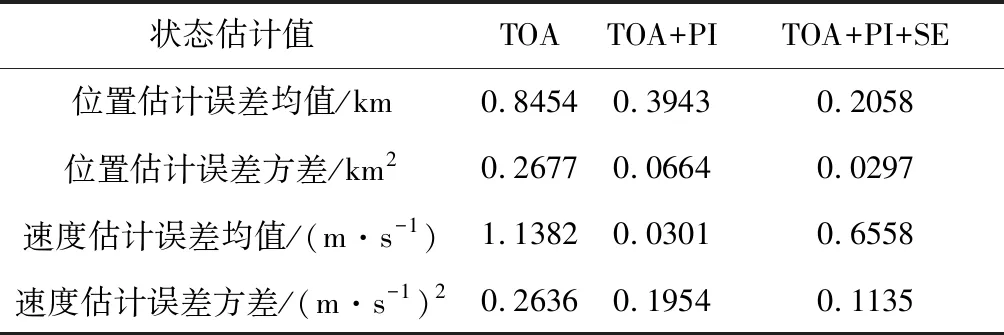
表3 ALOUETTE_1卫星状态估计值Table 3 State estimation value of ALOUETTE_1

从表3可以看出融合相位增量和星光仰角的X射线脉冲星导航系统的位置估计精度也能达到200 m 左右。对比卫星GPS_BII-04状态估计值，可知导航系统性能受轨道高度的影响较小，可为高中低不同轨道卫星提高导航服务，应用范围更广。

4 结 论

针对X射线脉冲星导航系统中过程噪声统计特性难以准确获取、滤波器估计性能不佳及导航精度低的问题，提出基于自适应差分卡尔曼滤波器的多信息融合算法。在传统X射线脉冲星信号计时观测的基础上，融合了恒星星光仰角信息及不同时刻之间的相位增量信息来提高导航精度。对高/低2种轨道卫星的状态估计结果表明：与仅使用脉冲星计时观测相比，融合相位增量观测量的方法能将卫星位置估计精度提高50%以上，速度精度提高25%以上；同时融合相位增量和星光仰角观测量，则可以获得更高的卫星状态估计精度，位置和速度精度分别提高了70%和40%以上。本文用ADDF将星光仰角和相位增量同时融入X射线脉冲星计时观测系统的方法，既提高了滤波器收敛速度，有效降低了导航误差，又扩大导航算法的应用范围，可为高低不同轨道卫星提供导航服务，具有很好的应用价值。