对失控翻滚目标逼近的神经网络自适应滑模控制
刘将辉,李海阳
(国防科技大学空天科学学院,长沙 410073)
0 引 言
近年来,航天器失联事件不断发生,如欧空局的Envisat卫星于2012年4月8日与地面失去了联系,印度发射的通信卫星GSAT- 6A于2018年3月31日进行最后一次轨道机动时与地面失去了联系。失联航天器一般处于低速无控制的自由翻滚状态,对在轨航天器的安全造成严重威胁。如果能对失控翻滚目标进行在轨维修检查、燃料加注和捕获,则具有重要的意义[1-3]。面向失控翻滚目标的逼近是实施上述任务的基础,追踪器需要对失控翻滚目标进行精确的位置跟踪和姿态同步。失控翻滚目标的非合作特性,大大增加了逼近过程的难度[4-5]。
针对这一问题,研究人员提出了各种非线性的控制方法[6]。文献[7]采用Smith模糊控制、文献[8]采用滑模控制、文献[9]采用人工视场法、文献[10]采用反馈线性法来设计航天器的相对运动。假设目标卫星的运动学是完全已知的,文献[11]设计了一种控制律,并给出了最优性准则,使跟踪器沿着所设计的轨迹向翻滚目标移动,直到两者之间保持相对静止。文献[12]利用逆动力学直接方法和非线性规划求解器序列梯度恢复算法研究了两个模拟航天器间协同对接策略的最小能量问题,并给出了一种近最优的制导策略。文献[13]基于双四元数的非线性和角速度反馈实现了追踪器对目标器的姿态同步。文献[14]阐述了具有通用目标的动力学和制导、导航与控制(GNC)方案,测试了基于线性二次型调节器(LQR)的位置跟踪控制器和角速度约束的比例微分(PD)姿态跟踪控制器。在有限时间控制和自适应控制策略的基础上,文献[15]实现了两航天器间的有限时间姿态同步与跟踪控制。采用状态相关的Riccati方程控制,文献[16]实现了两航天器间运动耦合的平动和旋转运动。文献[17]将滑模控制与逆最优控制相结合,考虑两航天器间的平移与姿态耦合,设计了鲁棒逆最优位置姿态控制器。文献[18]利用伪普法求得了追踪器与翻滚目标逼近的最小时间和最小能量消耗的最优轨迹。文献[19-20]针对非合作目标具有建模不确定性的问题,提出了一种具有标准可测信息的鲁棒自适应控制方法。文献[21-22] 应用模型预测控制器来控制追踪器逼近翻滚目标。文献[23]提出了一种基于非线性优化的运动规划方法,将安全成本放在首位,为追踪器接近非合作目标卫星提供一个安全的接近轨道。然而,多数文献存在以下不足:追踪器和目标器之间的相对位置和相对姿态耦合不完整,甚至忽略耦合作用;一般将标称轨迹或标称姿态单独设计以便对位置或姿态单独进行控制。设计参数的时候未考虑未建模动态和参数不确定性,甚至忽略外界扰动。
相比多层前馈反向传播(BP)网络,径向基函数(Radical basis function,RBF)网络具有良好的泛化能力,网络结构简单,避免不必要的和冗长的计算。RBF神经网络能够在一个紧凑集合任意精度下,逼近任何非线性函数[24]。滑模控制中,由于建模不确定性需要切换增益,这就容易造成抖振。本文在姿轨一体化模型中,考虑姿态和轨道耦合效应,设计标称轨迹和标称姿态,将滑模控制结合RBF神经网络逼近用于非线性系统的控制中,采用神经网络实现模型未知部分的自适应逼近。神经网络自适应律通过Lyapunov方法导出,通过自适应权重的调节保证整个闭环系统的稳定性和收敛性。仿真结果表明,本文所设计的神经网络自适应滑模控制器能够使追踪器快速、安全地逼近失控翻滚目标器,整个控制过程中无抖振问题,追踪器输出力矩和控制加速度连续平滑。
1 相对运动动力学方程
1.1 相对轨道动力学


图1 相对运动坐标系统Fig.1 Relative motion coordinate system
在目标航天器轨道坐标系下,选用非线性的T-H方程描述追踪航天器与目标航天器的相对运动[25]
(1)
(2)
(3)
其中,n为目标航天器的平均轨道角速度,e为目标航天器轨道偏心率。由式(1)可得到如下形式的非线性轨道相对运动方程
(4)
式中:
1.2 相对姿态动力学
根据刚体动量矩定理,可得到航天器姿态动力学方程
(5)
其中,J为航天器的转动惯量,ω为航天器姿态运动角速度矢量,τc为航天器姿态控制力矩,τd为航天器所受的外部未知有界干扰力矩,τg为航天器所受的重力梯度力矩,τg表达式为
(6)
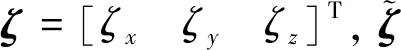
(7)
由于追踪航天器与失控翻滚目标航天器进行姿态同步旋转的过程中存在大角度机动,为避免姿态控制中出现奇异,本文使用四元数描述航天器的姿态运动。下面基于误差四元数推导追踪航天器和目标航天器的相对姿态动力学模型。
设航天器当前姿态四元数为q,期望姿态四元数为qd,误差四元数qe的表达式为
(8)
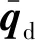
(9)
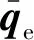
设追踪器当前的角速度矢量为ω,期望的姿态角速度矢量为ωd,角速度误差矢量为ωe,其表达式为
ωe=ω-Meωd
(10)
(11)
其中,
(12)
式中:G=ωe+Meωd。

(13)
对式(13)两边求导可得
(14)
基于误差四元数,由式(14)可得到如下形式的航天器相对姿态动力学方程
(15)
式中:
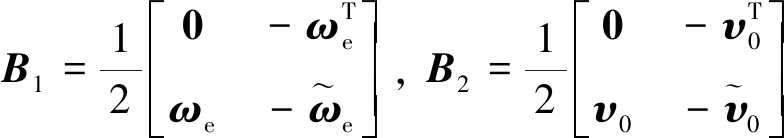
1.3 姿轨一体化动力学模型
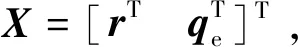
(16)
式中:
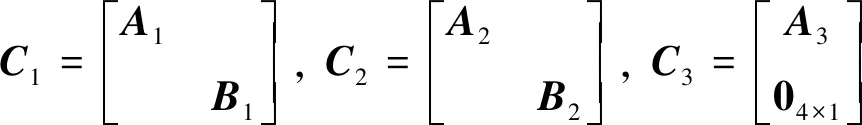
2 标称轨迹和标称姿态设计
2.1 标称轨迹设计
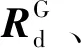
根据本文对目标器轨道坐标系的定义,由惯性坐标系OEXEYEZE至目标器轨道坐标系OTXTYTZT的姿态转移矩阵MIG为
(17)
式中:
(18)
(19)
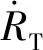
(20)
(21)
(22)
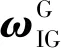
(23)
(24)
(25)
2.2 标称姿态设计
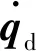
(26)
其中,
(27)
式中:
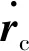
(28)
(29)
(30)
(31)
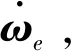
3 控制器设计
3.1 滑模函数
考虑系统中存在未建模动态及参数不确定性,由式(16)得到进一步的姿轨一体化模型
(Cd3+ΔC3)+C4(u+d)
(32)
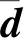
(33)
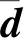
(34)
基于式(34)所建立的姿轨一体化动力学模型,通过控制输入u来对追踪器逼近过程进行控制。取
(35)
式(34)写成状态方程的形式为
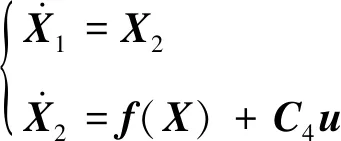
(36)

e=X1-Xd
(37)
(38)
滑模函数设计为
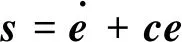
(39)
其中,c为滑模函数系数,c=diag(c1,…,c7),ci>0,i=1,2,…,7。则
(40)
3.2 RBF神经网络原理

(41)
(42)
(43)
3.3 控制器设计与稳定性分析
由于
(44)
定义Lyapunov函数为
(45)
其中,γ>0。
于是
(46)
设计控制律为
(47)
其中,η=diag(η1,…,η7),ηi>0,i=1,2,…,7, sgn(s)=[sgn(s1),…,sgn(s7)]T,则
(48)
其中,κ=[η1,…,η7]T,取ηi>|εi|max,i=1,2,…,7,自适应律为
(49)
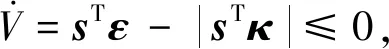
4 仿真分析
假设目标航天器在空间中处于失控翻滚状态,且不存在轨道机动。考虑J2项摄动和大气阻力的影响,仿真采用高精度数值积分轨道模型。目标航天器的轨道六根数为:a=6739200 m,e=0.005,i=51.6°,Ω=315°,ω=41°,f=320°。追踪器在距目标器质心15 m时对目标器进行逼近,终端逼近位置距目标器质心1 m,逼近期间假设追踪器和目标器的转动惯量不随时间而变化。

表1 仿真参数Table 1 Simulation parameters
设追踪器受到的外部有界摄动加速度ad和外部有界摄动力矩τd分别为[26]
(50)
(51)
式(50)和(51)中,ωo为追踪器轨道角速度,{ad1,ad2,ad3}与{τd1,τd2,τd3}满足均值为0且方差为υ=10-5高斯分布N(0,υ)。RBF神经网络滑模控制器参数如表2所示。

表2 神经网络滑模控制器参数Table 2 Neural network sliding mode control parameters
需要说明的是,表2中的高斯基参数pj和bj由网络输入X1和X2的实际范围来设计,本文采用了尝试法,并没有进行最优化处理。仿真结果如图2~图7所示。

图2 误差四元数、位置偏差和速度偏差Fig.2 Error quaternion, relative position and relative velocity
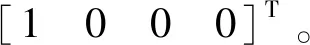
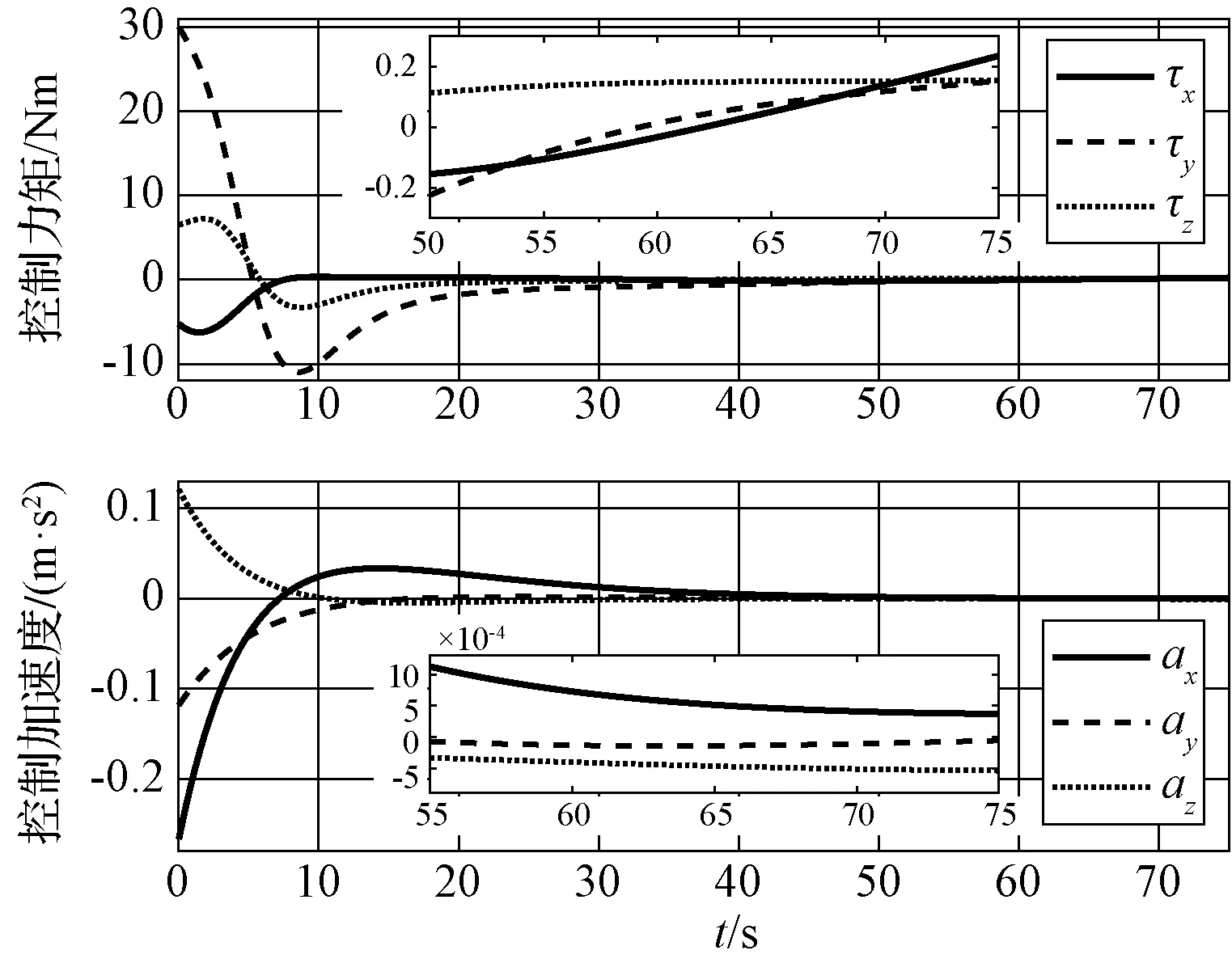
图3 追踪器的控制力矩和控制加速度Fig.3 Control torque and control acceleration of the chaser
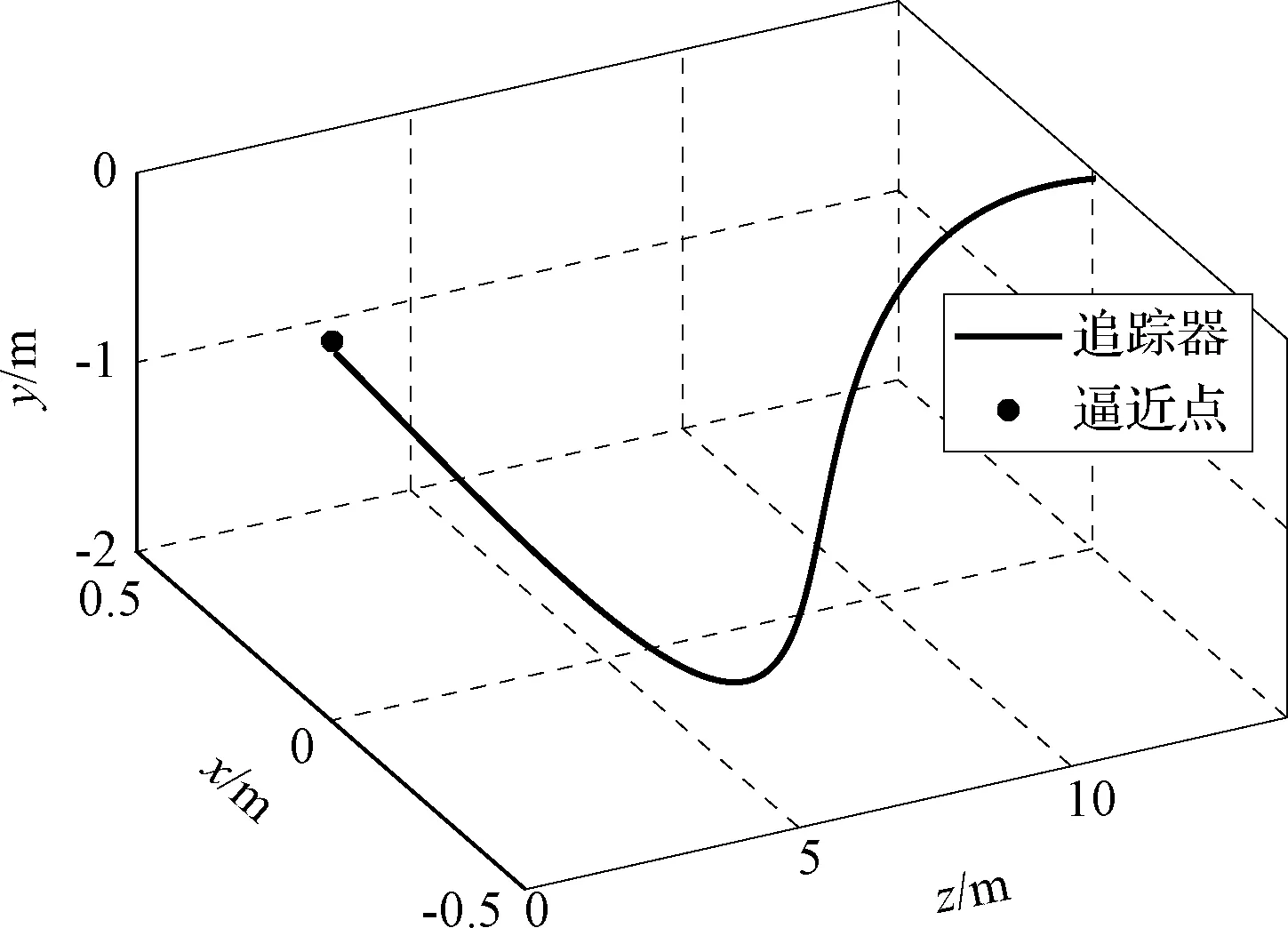
图4 三维空间中追踪器与目标逼近点的相对位置Fig.4 Relative position of the chaser and approach point in three-dimensional space
图3为追踪器的控制力矩和控制加速度变化曲线。在神经网络自适应滑模控制器的作用下,追踪器x与z方向输出的控制力矩变化较小,y方向输出的控制力矩较大,一段时间之后,各方向的控制力矩趋向于0,这是因为追踪器已经跟上了目标器的姿态,追踪器和目标器一起做相同的姿态运动。当完成姿态捕获后,后续所需的控制力矩极小;追踪器需要将其质心位置始终保持在逼近点的轴线上,初始时刻,追踪器距逼近点较远,所以初期所需的控制加速度较大。随着两者的距离逐渐减小,其控制加速度呈现振荡减小的趋势,最后趋向于0。整个过程中,控制力矩和控制加速度较为平缓,没有出现抖振现象,神经网络自适应滑模控制器成功克服了传统滑模控制器抖振特性的影响。
图4为追踪器与逼近点的三维相对位置的变化曲线,与常规交会对接任务最后逼近段的准直线相对运动轨迹不同。由于目标航天器处于失控翻滚状态,追踪器逼近轨迹始终位于目标器体坐标系x轴上,所以追踪器三维相对运动为同步指数减速逼近曲线。
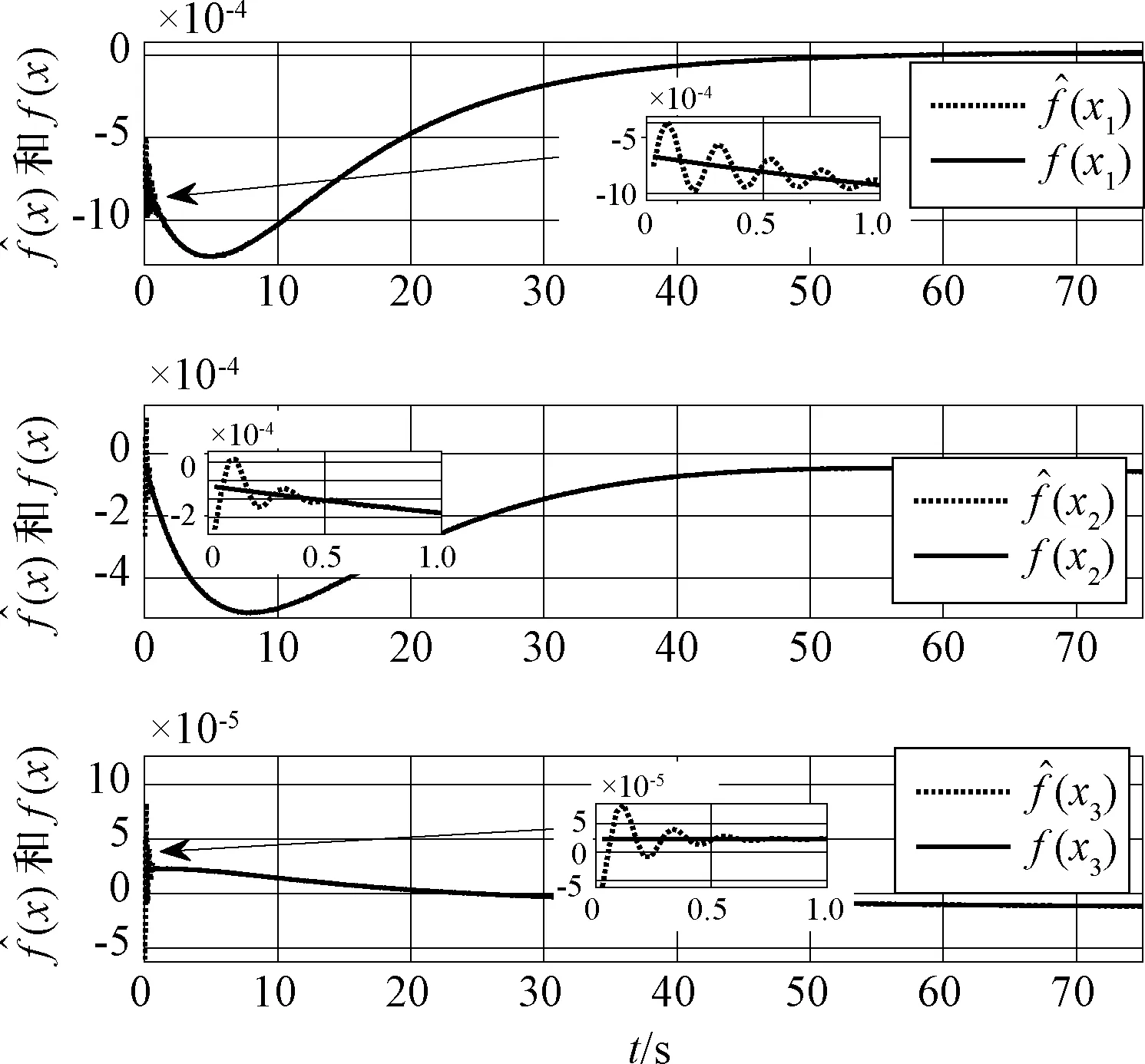
图5 f(x)和估计值Fig.5 f(x) and the estimation
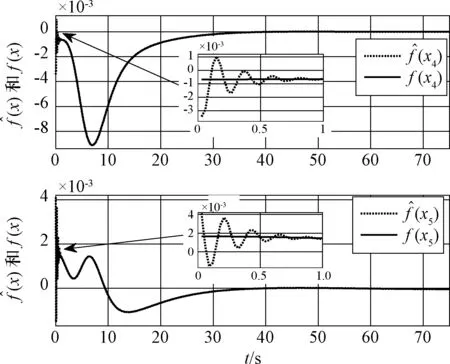
图6 f(x)和估计值Fig.6 f(x) and the estimation
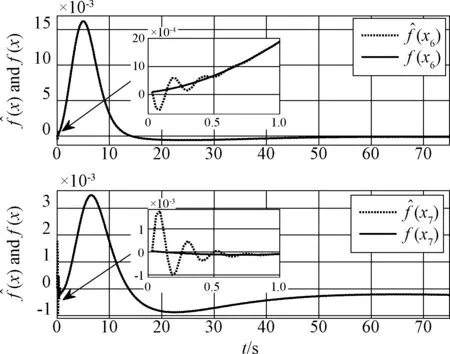
图7 f(x)和估计值Fig.7 f(x) and the estimation
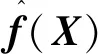
为了说明所设计控制器的优越性,将RBF神经网络滑模控制器与传统滑模控制器进行对照。在没有RBF神经网络自适应条件下,式(47)在传统滑模控制中可表示为
(52)
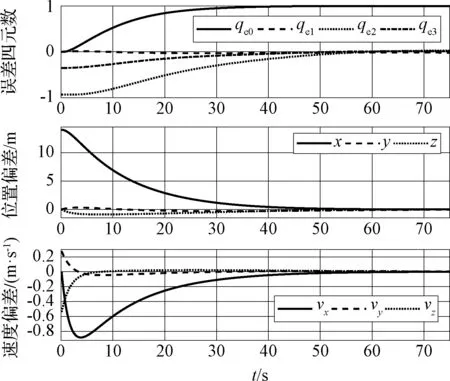
图8 滑模控制器下的误差四元数、位置偏差和速度偏差Fig.8 Error quaternion, relative position and relative velocity under sliding mode control
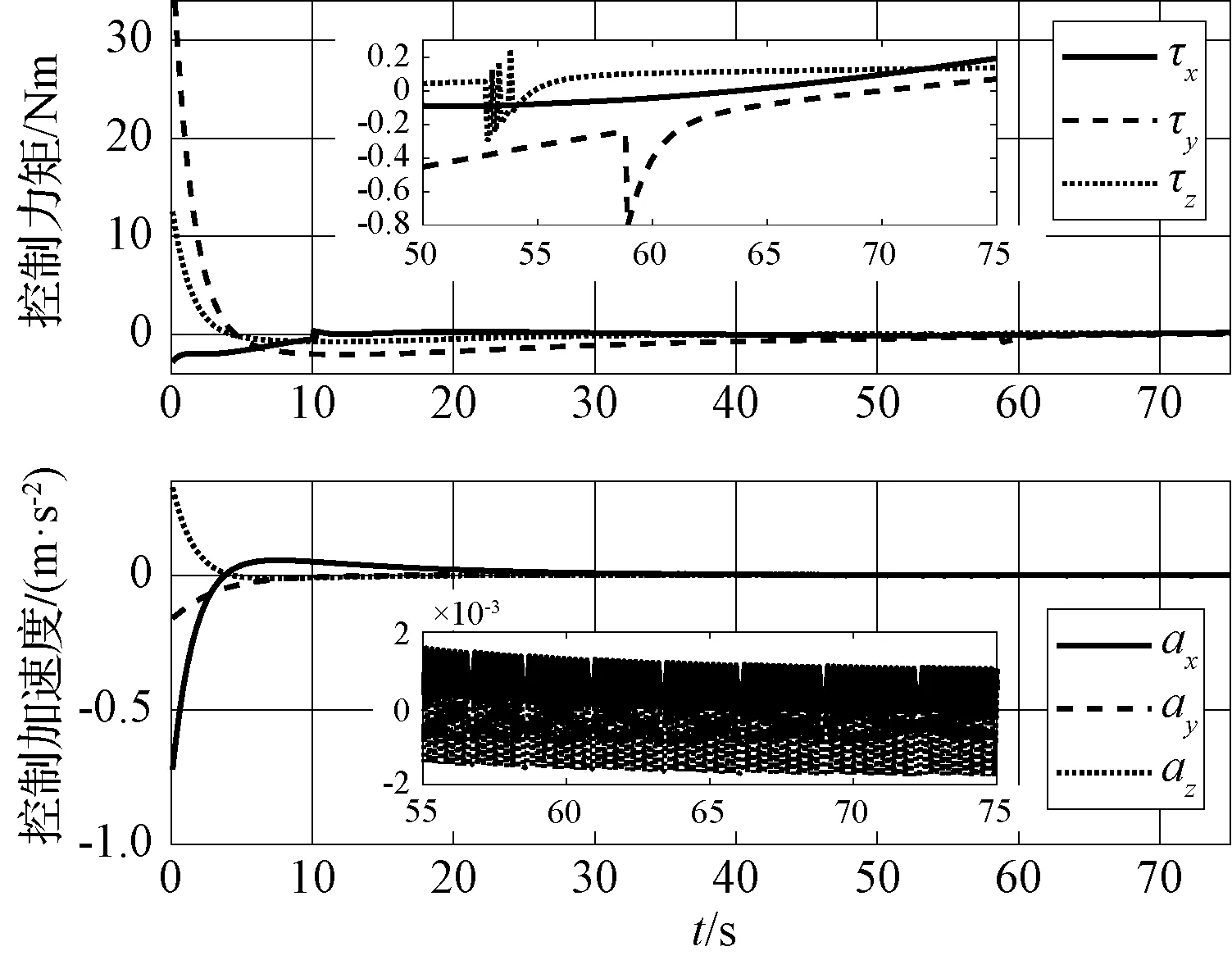
图9 滑模控制器下的追踪器的控制力矩和控制加速度Fig.9 Control torque and control acceleration of the chaser under sliding mode control
通过将图8~图9与图2~图3对比可知,传统滑模控制器完成姿态同步需要约56 s,比RBF神经网络滑模控制器慢21 s。传统滑模控制器下的控制力矩和控制加速度出现了明显的抖振现象,初始控制加速度比RBF神经网络滑模控制器下的更大。
5 结 论
本文研究了逼近失控翻滚目标的相对轨道和相对姿态的六自由度耦合控制问题,建立了两航天器相对运动的六自由度耦合的一体化模型,对逼近翻滚目标的标称轨迹和标称姿态进行了分析和设计。考虑外部干扰、系统不确定性以及滑模控制中的抖振等因素,推导了六自由度逼近的神经网络自适应滑模控制器并给出了稳定性证明。仿真结果表明,该控制器能够有效克服系统不确定因素的影响。追踪器按照设计的标称轨迹对目标实现了快速逼近,保证了逼近过程的安全性。控制过程中产生的控制力矩和控制加速度连续平滑,克服了抖振问题。

