临近空间高超声速滑翔弹双通道跟踪算法

喻晨龙，谭贤四，曲智国，王 红，谢 非

(1.空军预警学院防空预警装备系，武汉 430019； 2.长江勘测规划设计研究院，武汉 430019)

0 引 言

当前可能用于作战的临近空间高超声速武器主要有两类：①高超声速助推滑翔导弹，典型有HTV-2和AHW；②高超声速巡航导弹，典型有X-43A、X-51A、“锆石”、“布拉莫斯-2”[1-3]。面对日益临近的潜在威胁，如何更好的跟踪这些目标成为亟待解决的现实问题。

关于临近空间高超声速滑翔弹的跟踪研究主要包括跟踪模型和滤波算法。当跟踪目标的运动状态是非线性时，需要用到EKF、UKF和CKF等非线性滤波算法[4-6]，当跟踪目标处于强机动状态时，常常采用交互多模型(IMM)滤波算法[7-8]。然而，这些都取决于对目标运动状态的数学描述，也就是目标的状态模型，好的状态模型不仅可以提高跟踪精度，还能够简化跟踪过程提高运算速度。

跟踪的状态模型的建立有两种方法:①从飞行受力的角度考虑，结合推力模型、气动力模型、大气模型等建模得到目标运动学方程[9-10]。文献[11]对再入飞行器的气动力进行了深入分析，提出把气动力投影到速度坐标系实现解耦，然后利用非线性Kalman滤波器进行状态估计。②在弹道分析的基础上，对目标的某些运动参数变化规律合理假设，对随机过程噪声加以描述[12-13]。文献[14]指出临近空间高超声速滑翔目标的位置轨迹曲线呈现明显的周期特性,用正弦自相关随机过程来描述目标的加速度变化规律建立了Sine Wave模型。

关于目标的机动模型，Li和Jilkov等[15-18]的一系列文章对此进行了详细论述，他们指出跟踪的状态模型可以归为两大类:①坐标解耦的Markov模型，这包括CA、CV、CS、Singer、Jerk等;②坐标耦合的空间模型，这包括2D水平运动模型和3D运动模型，也就是CT模型。当跟踪模型的状态量参数属于同一个位置域或角度域时，模型是线性的，然而，空间上的CT模型通常转向率未知，需要进行状态扩维，使得状态模型非线性，大大降低了跟踪精度。关于目标的三维跟踪方法，张翔宇等在文献[19]中提出将量测数据转换到经纬高坐标系，在经纬平面采用基于点迹归并和凝聚的线性Kalman滤波器，在高度方向采用Singer+CA+CT组成的IMM滤波器并行跟踪，然后合并数据输出三维跟踪滤波结果。

在本文中，我们通过角度域的参数描述目标的运动状态，建立状态模型，它们具有比位置参数更明显的变化规律，能更准确地近似目标的真实运动。在角度域中，由于代表纵向机动的航迹倾角存在明显周期性，代表横向机动的航向角呈近似线性，提出在纵向通道和横向通道分别建立角度域参数的Markov模型。虽然航迹倾角和航向角的规律显著，但是在雷达观测坐标系下是不可见的。在纵向观测平面，倾角变化率与航迹倾角变化率近似，可以用倾角替代航迹倾角建立Markov模型，进而估算出角度变化率，把它输入到随后的空间CT模型中，使得其状态模型线性。在横向观测平面，方位角是可观测角，基于方位角建立Markov模型，进而估算出每一时刻目标的横向偏移。通过量测转换，双通道并行跟踪和输出合并三个步骤，实现了目标位置状态的三维跟踪。最后设置了一个仿真场景，分析了系统参数的取值范围和算法的鲁棒性，与现有的临近空间高超声速目标跟踪算法相比，该算法具有较高的跟踪精度。

1 目标运动特性

1.1 参考坐标系和坐标平面

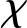
坐标平面如图2所示，图2(a)、(b)分别表示纵向观测平面(Longitudinal observation plane, LOP)和横向观测平面(Horizontal observation plane,HOP)。LOP与ENU坐标系的OSySzS平面重合，HOP与ENU坐标系的OSxSyS平面重合。Tra表示目标弹道，(x,y,z)表示目标位置，(r0,θ,ϑ)代表测量得到的距离、俯仰角、方位角，γ表示航迹倾角，β表示航程角，φ表示倾角。P′表示质心的投影，R为地球半径，r为地心距。

图1 ECEF和ENU坐标系Fig.1 ECEF and ENU Coordinate system

图2 观测平面Fig.2 Observation planes

1.2 运动轨迹特性分析

临近空间高超声速滑翔弹飞行全程主要受到地球重力，气动力和离心力的作用，当这三个力在纵向上的分量的合力为0时，构成平衡滑翔条件，轨迹为无震荡的平坦光滑曲线，运动参数(速度、高度、航迹倾角)之间存在特定的解析关系，当合力不为0时，不满足平衡滑翔条件，轨迹为跳跃震荡曲线，运动参数之间不存在近似的解析关系，只能依据目标的三自由度弹道方程，通过数值仿真分析运动参数的变化规律[20]。

目标位置域的参数包括高度和速度，目标角度域的参数包括航迹倾角和航向角。高度衰减震荡，速度成阶梯式下降，航迹倾角为小量且周期性变化，航向角台阶式增大。我们还可以得到如下结论：

1)轨迹可以分解到纵向和横向平面。控制量攻角决定着飞行器纵向上的机动，控制量倾侧角决定着飞行器横向上的机动，在纵向上有机动强度很大的跳跃运动，在横向上则是机动强度较弱的偏移运动。机动强度越大跟踪模型的数学描述越复杂，跟踪的关键在纵向上。

2)角度域的参数具有较为确定的显著规律。航迹倾角反映着目标的纵向机动，始终保持着周期性变化，航向角反映着目标的横向机动，随着倾侧角的增大偏移越来越大。高度和速度不能直接反映目标横纵向机动运动。

3)当倾侧角σ=0时，目标轨迹横向上不发生偏移，航向角的变化率维持恒零，仅在纵向上有跳跃机动。当倾侧角σ不为零时，目标轨迹不仅在纵向上有跳跃机动，在横向上也有偏转机动。目标处于跳跃滑翔状态时，在纵向上的跳跃机动是始终存在的，在横向上的偏移转弯则受到倾侧角控制，对应到角度域的参数上来说，航迹倾角的变化率是始终存在的，航向角的变化率受倾侧角控制。

因此，在跟踪高超声速目标时我们可以从角度域参数着手，把目标轨迹投影到纵向观测平面和横向观测平面，基于航迹倾角和航向角分别建立纵向通道和横向通道的跟踪模型，然后并行跟踪滤波。但是，航迹倾角和航向角在ENU坐标系下是不可见的，不能直接用于建模，要在LOP和HOP平面内寻找替代量，参与模型的建立。

如图2(a)，在LOP中有如下关系：

(1)

对式(1)的第1个式子求导：

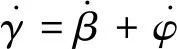
(2)

从式(2)可知航迹倾角变化率、倾角变化率、航程角变化率之间存在加法关系，需要明确这三个角中的哪一个可以作为替代量，用来建立纵向通道的跟踪模型。

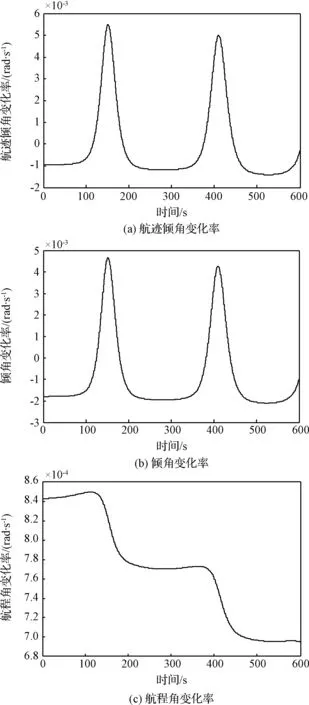
图3 纵向观测平面的角度变化率Fig.3 Change rate of angles in longitudinal observation plane

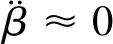
(3)

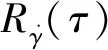
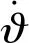
(4)

因此，在HOP平面，用方位角代替航向角，把方位角变化率描述为正弦自相关随机过程，建立横向通道的机动模型。

2 跟踪模型与算法

在上文中，我们找到了角度域中的倾角和方位角参数，代替原来的航迹倾角和航向角，分别在纵向通道和横向通道建立跟踪模型。在建立角度域模型时，均把角度变化率描述为零均值正弦自相关函数，构造了角速度正弦波(Angular velocity sine wave, AVSW)模型。在纵向通道，为了得到目标的位置参数，在AVSW后端嫁接了一个CT模型，把角度变化率输入到CT模型中。在横向通道，直接输出方位角估计。系统通过量测转换，双通道并行滤波和输出合并，实现了目标的三维跟踪，其结构如图4所示。

图4(a)描述了系统的总体结构，在跟踪过程中，首先把量测数据由球坐标转换到直角坐标，然后分类输入到纵向通道和横向通道，最后通过一个数据合并模块后，输出目标的三维状态估计。图4(b)描述了纵向通道的AVSW-CT模型结构，输入是经过量测转换后的LOP平面数据，该模型包括一个角度子滤波器和一个位置子滤波器，其中角度子滤波器的状态模型为倾角变化率的Markov模型，位置子滤波器的状态模型为CT结构的空间模型。AVSW模型作用于角度域，CT模型作用于位置域。图4(c)描述了横向通道的AVSW模型结构，输入为目标的方位角观测值，该模型包含一个角度滤波器，其状态模型为方位角变化率的Markov模型。图4(d)描述了双通道的合并输出方法，纵向通道输出目标纵向的位置和速度，横向通道输出横向的方位角，先得到目标的横向偏移，然后得到目标的三维位置估计。其详细的论述见下文。

2.1 纵向通道AVSW-CT模型

不论控制量如何变化，纵向上的跳跃机动始终存在，AVSW-CT模型用来描述目标在纵向上的机动运动，它由一个角度子滤波器和一个位置子滤波器组成。

1)角度子滤波器的状态模型

图4 系统架构Fig.4 System frame

角度滤波器的状态模型也就是AVSW模型，其推到过程如下。假设目标的倾角变化率为一零均值的正弦随机信号，其自相关函数为：

(5)

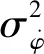
这是一有色噪声信号，其功率谱密度为：

(6)

因此倾角变化率的二阶Markov模型为：

(7)

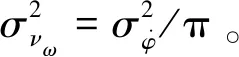
(8)

那么，倾角变化率的离散时间状态方程为：

Xω(k+1)=AωXω(k)+νωc(k)

(9)

其中：

(10)

过程噪声νωc具有的协方差为：

(11)

其中：

(12)

2)角度子滤波器的量测模型

纵向通道的跟踪在LOP平面进行，首先需要把以球坐标形式表示的ENU坐标系下的观测数据投影到LOP平面。这里采用无偏转换[14]，实现球-直坐标转换。

然而，得到的位置属性的量测数据不能直接输入到角度子滤波器，需要根据式(1)的第二个式子计算，把它转换为角度格式。

那么，角度子滤波器的等效量测模型为：

Zω,k=HωXω,k+κω,k

(13)

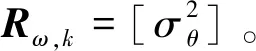
角度子滤波器输出角度变化率，输入到位置子滤波器，使得其状态模型线性。

3)位置子滤波器的状态模型

位置子滤波器的状态模型也就是CT模型，是LOP中角度关系在位置维度的映射。在图2(a)中有如下关系：

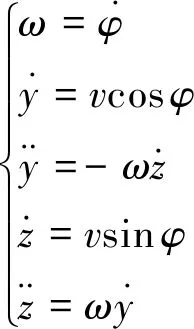
(14)

位置的连续时间状态方程为：

(15)

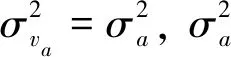
Xa(k+1)=AaXa(k)+νac(k)

(16)

式中：

(17)

过程噪声νac具有的协方差为：

(18)

其中：

(19)

4)位置子滤波器的量测模型

位置子滤波器的等效量测模型为：

Za,k=Ha,kXa,k+κa,k

(20)

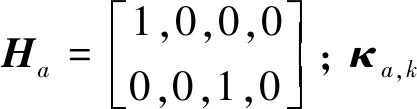
位置子滤波器的输出为目标的位置和速度。

2.2 横向通道AVSW模型

当倾侧角为零时，目标仅在纵向平面跳跃，当倾侧角不为零时，目标除了在纵向上跳跃，还在横向上偏转，AVSW模型用来描述目标在横向上的机动运动，它包含一个角度滤波器。

1)角度滤波器的状态模型

角度滤波器的状态模型和上文所述的AVSW模型相同。假设方位角变化率为一零均值的正弦随机信号，其自相关函数为：

(21)

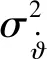
(22)

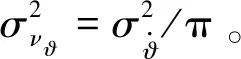
Xϑ(k+1)=AϑXϑ(k)+νϑc(k)

(23)

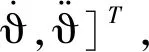
2)角度滤波器的量测模型

横向通道的输入为目标的方位角观测序列，等效量测模型表示为：

Zϑ,k=HϑXϑ,k+κϑ,k

(24)

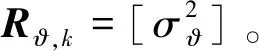
角度滤波器的输出为方位角估计值。

2.3 输出合并

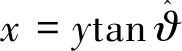
(25)

因此k时刻目标在x轴上的横向的位置估计为：

xk=Xa(1,k)tan(Xϑ(1,k))

(26)

2.4 跟踪算法流程

综上可见，整个系统均可采用线性的kalman滤波器跟踪，跟踪算法的步骤如下：

输入：ENU坐标系下的观测序列。

输出：ENU坐标系下的状态估计。

步骤1：量测数据预处理

步骤1.1：将方位角原始测量数据输入到横向通道，直接获得角度格式的量测序列{zϑ,k}。

步骤1.2：将观测值从球坐标系转换到直角坐标系，提取y轴和z轴数据，组成位置格式的量测序列{za,k}。根据式(1)的第2个式子，将位置格式的量测序列{za,k}转换成角度格式的量测序列{zω,k}。

步骤2：线性滤波器并行跟踪

步骤2.1：横向通道跟踪

假设k-1时刻的状态向量和协方差矩阵分别为Xϑ,k-1/k-1和Pϑ,k-1/k-1。线性Kalman滤波：

(27)

(28)

(29)

步骤2.2：纵向通道跟踪

步骤2.2.1：角度子滤波器跟踪：

假设在k-1时刻的状态向量和协方差矩阵分别为Xω,k-1/k-1和Pω,k-1/k-1。线性Kalman滤波：

(30)

(31)

(32)

步骤2.2.2：驱动位置子滤波器跟踪：

提取角度子滤波器输出状态的第二个分量ω(k-1)=Xω(2,k-1)。利用角度变化率分别生成状态转移矩阵Aa,k-1和过程噪声协方差矩阵Qa,k-1。

假设在k-1时刻的状态向量和协方差矩阵分别为Xa,k-1/k-1和Pa,k-1/k-1。线性Kalman滤波：

(33)

(34)

(35)

步骤3：合并输出。

根据式(26)生成k时刻在x轴上的位置分量，合并状态量，输出目标的位置和速度估计。

3 仿真校验

3.1 仿真场景假设

参考美国官方公布的HTV-2的基本试验情况，本文假设如下仿真场景：升力式滑翔目标由火箭助推至80 km高空后释放，分离时目标的位置为E110°N0°，再入攻角为11.6°，倾侧角为20°，速度为20 Ma，航迹倾角和航向角为0°。假设某型雷达部署在E112°N10°，其参数如表1所示。

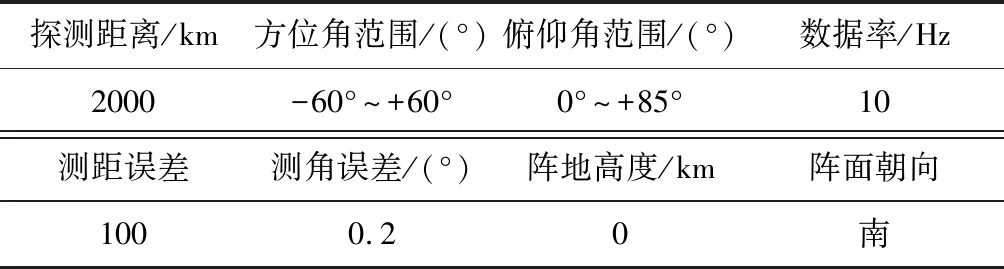
表1 雷达参数Table 1 Radar parameters

由于地球曲率影响，雷达在ENU坐标系下只观测到了目标的部分轨迹，如图5所示。

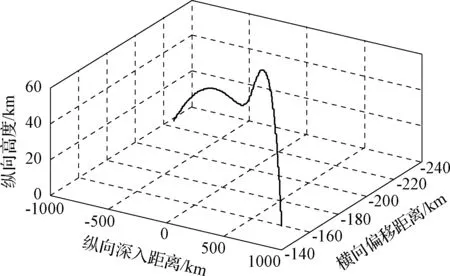
图5 ENU坐标系下的目标轨迹Fig.5 Trajectory in ENU coordinate system

从图5可看出，目标在(-975 km, -225 km)处穿越地平面进入雷达视线范围，然后在纵向上跳跃运动，同时在横向上发生偏移，最后在(770 km，-160 km)处进入地平面以下，离开雷达视线范围。整个过程中目标的飞行速度很快，观测的时间很短，不到400 s。

3.2 模型参数设置

首先设置纵向通道的模型参数α0。假设AVSW-CT模型中的角度子滤波器的角度分布的误差标准差为10-8，位置子滤波器的位置分布的误差标准差为103，参数α0分别为10-1、10-2、 10-3、 10-4、 10-5，进行100次蒙特卡洛仿真，得到结果如图6和图7所示。

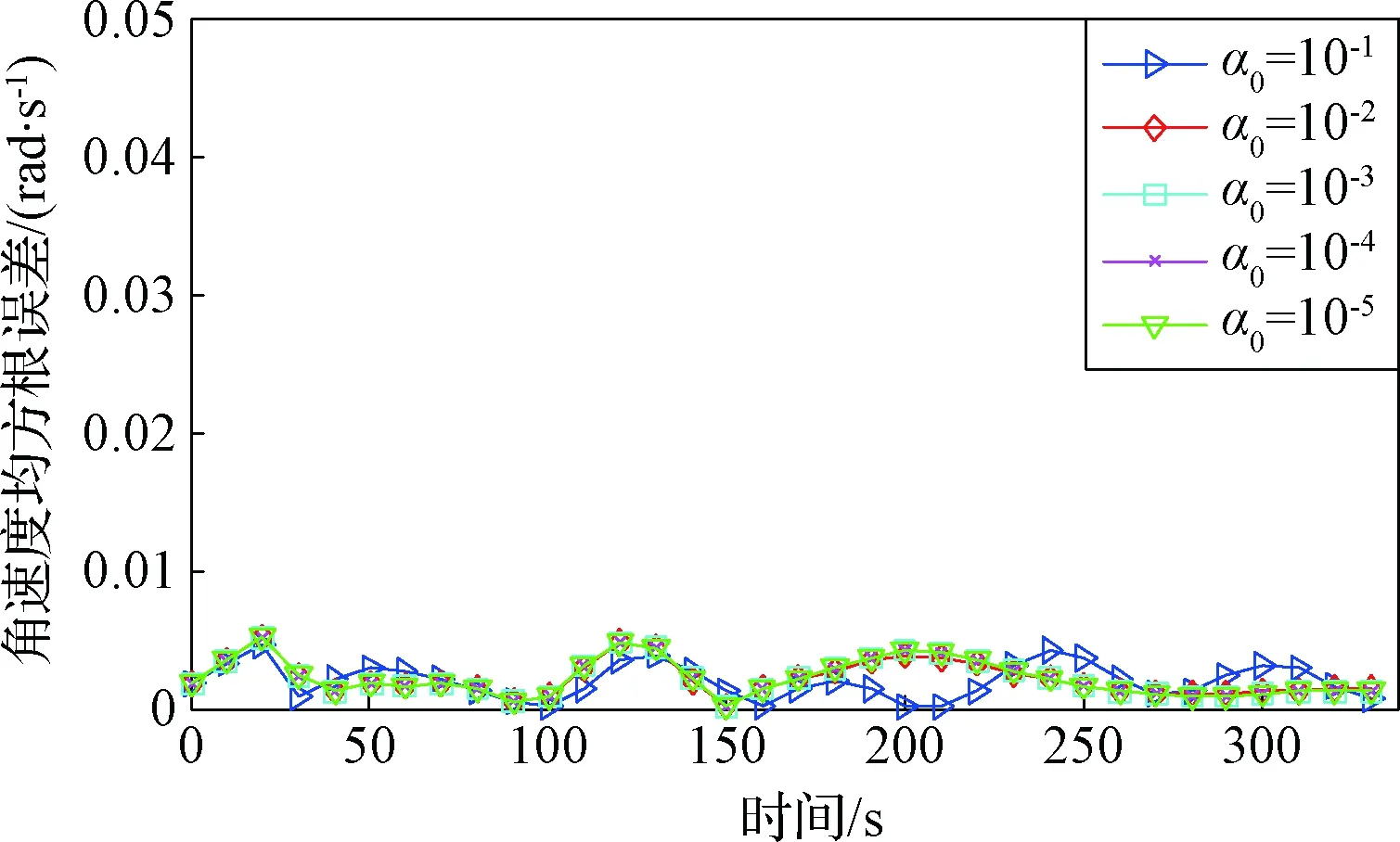
图6 纵向通道角度子滤波器输出误差(α0)Fig.6 Output error of longitudinal channel angle sub-filter (α0)

图7 纵向通道位置子滤波器输出误差(α0)Fig.7 Output error of longitudinal channel position sub-filter (α0)

图6为角度子滤波器的输出误差，图7为位置子滤波器的输出误差。从图6和图7中对比可知，AVSW-CT模型具有较好的跟踪精度，当α0≤10-2时，角速度和位置的估计更精确。

然后设置横向通道的模型参数α1。假设AVSW模型中的角度滤波器的过程噪声误差标准差为10-4，参数α1分别为10-1、10-2、 10-3、 10-4、 10-5，进行100次蒙特卡洛仿真，得到结果如图8所示。

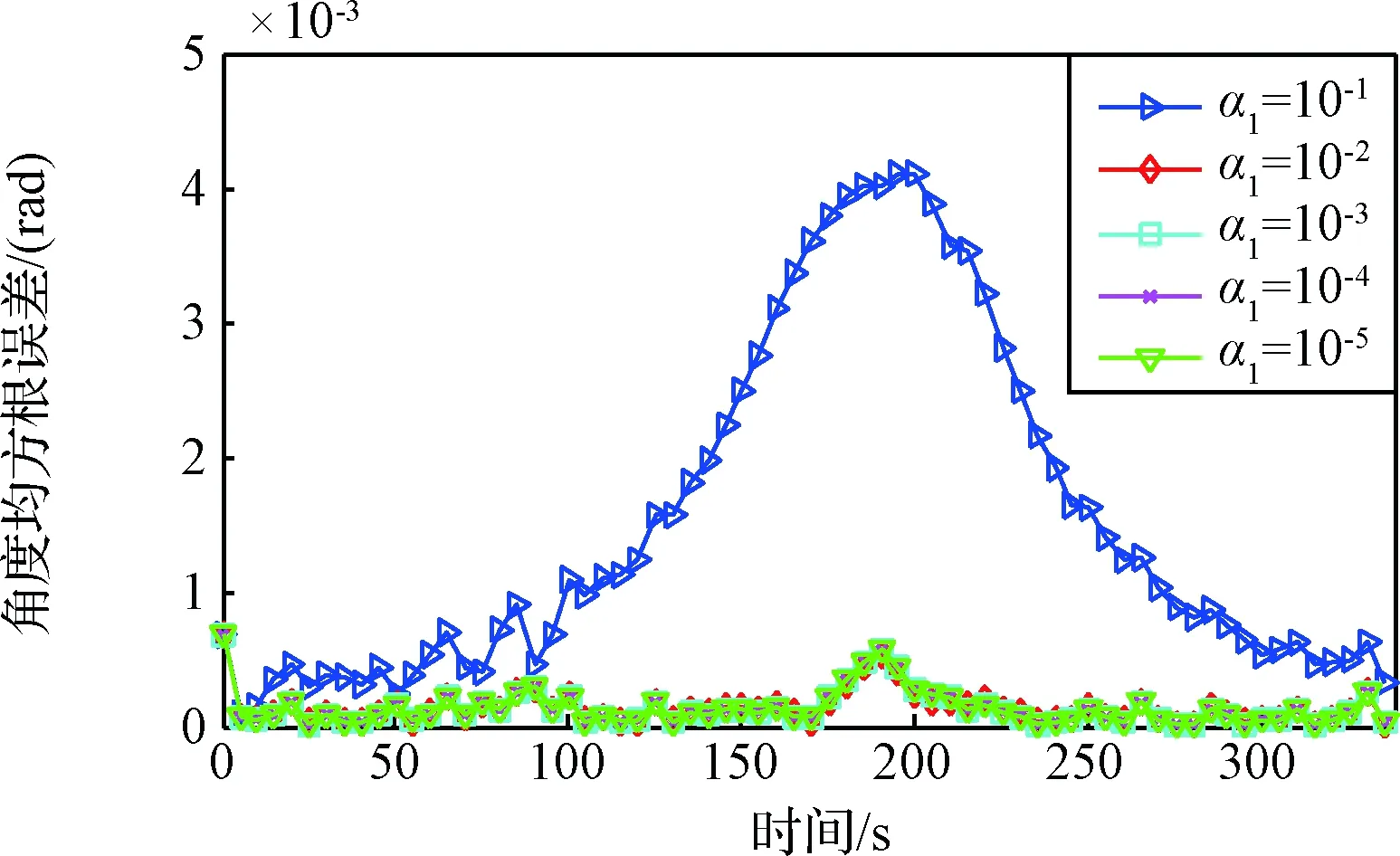
图8 横向通道角度滤波器输出误差(α1)Fig.8 Output error of horizontal channel angle filter (α1)

图8为角度滤波器的输出误差。从图8中对比可知，AVSW模型具有较好的跟踪精度，当α1≤10-2时，方位角估计更精确。

3.3 仿真试验结果与分析

1)鲁棒性分析

通过仿真试验分析模型过程噪声对跟踪精度的影响，首先是纵向通道的角度子滤波器。假设AVSW-CT模型中的参数α0为10-3，角度子滤波器的过程噪声标准差σω分别为10-6、 10-7、 10-8、 10-9、 10-10，进行100次蒙特卡洛仿真，得到结果如图9所示。

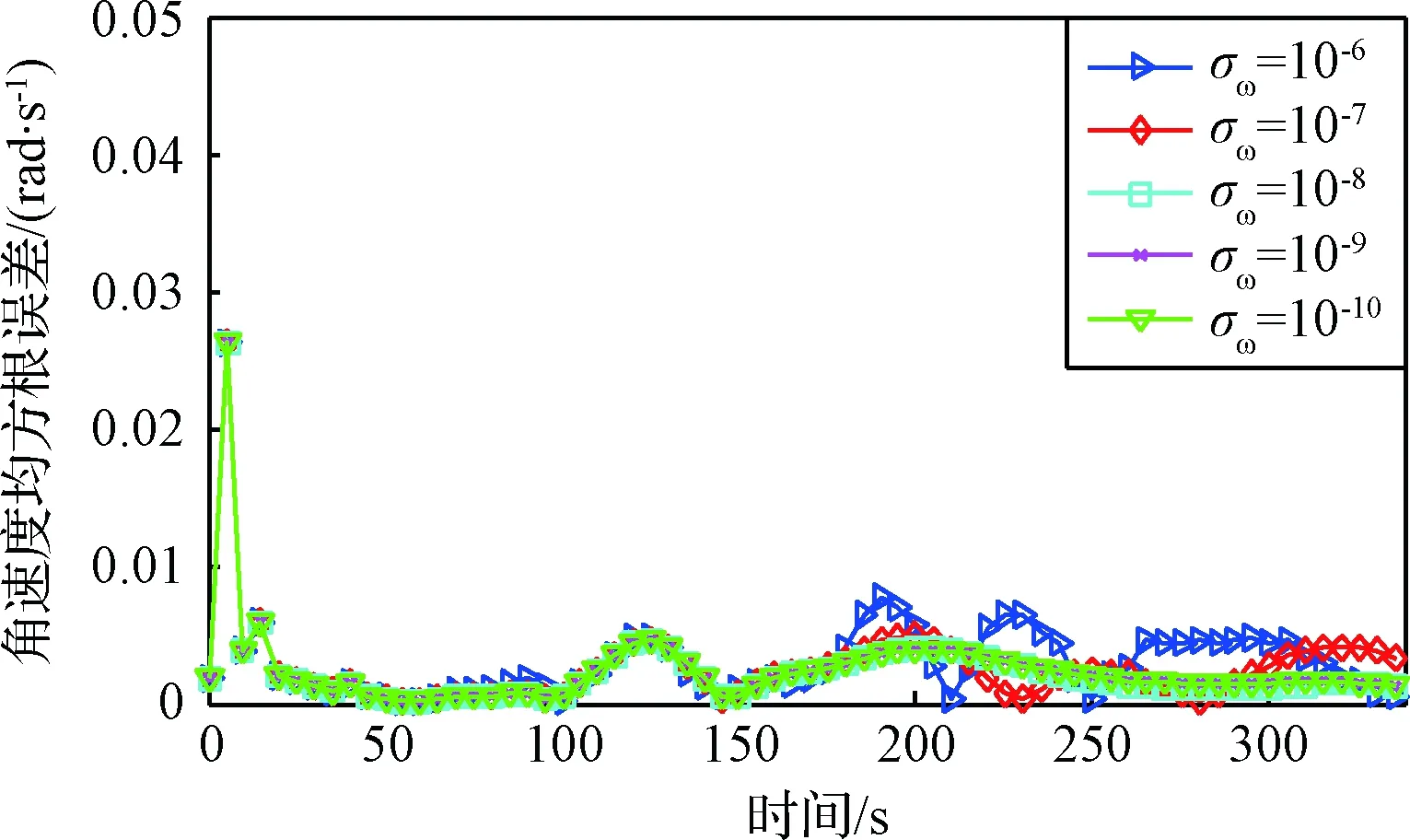
图9 纵向通道角度子滤波器输出误差(σω)Fig.9 Output error of longitudinal channel angle sub-filter (σω)

图9为角度子滤波器的输出误差。从图中的对比可知，当σω≤10-8时，跟踪精度更高。

然后分析纵向通道的位置子滤波器。假设AVSW-CT模型中的参数α0为10-3，角度子滤波器的过程噪声标准差σω取10-8，位置子滤波器的过程噪声标准差σa分别为10、 102、 103、 104、 105进行100次蒙特卡洛仿真，得到结果如图10所示。

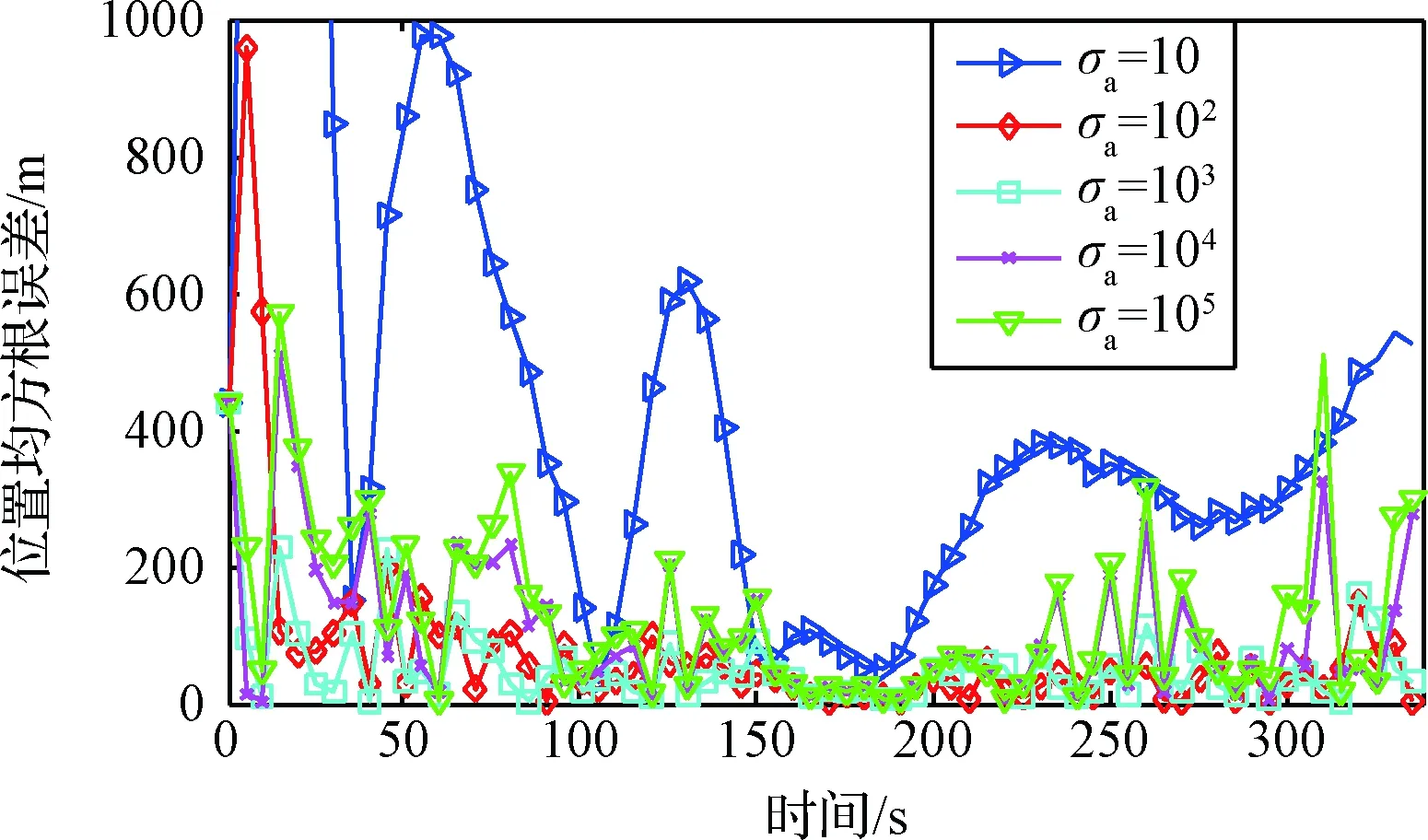
图10 纵向通道位置子滤波器输出误差(σa)Fig.10 Output error of longitudinal channel position sub-filter (σa)

图10为位置子滤波器的输出误差。从图中的对比可知，噪声对跟踪精度的影响较明显，当σa∈[1001000]时，跟踪精度最佳。

最后分析横向通道的角度滤波器。假设AVSW模型中的参数α1为10-3，角度滤波器的过程噪声标准差σϑ分别为10-1, 10-2, 10-3, 10-4, 10-5，进行100次蒙特卡洛仿真，得到结果如图11所示。

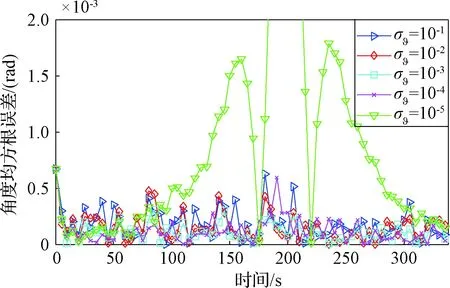
图11 横向通道角度滤波器输出误差(σϑ)Fig.11 Output error of horizontal channel angle filter (σϑ)

图11为角度滤波器的输出误差。从图中的对比可知，噪声对跟踪精度的影响较明显，当σϑ∈[10-410-3]时，跟踪精度最佳。

2)跟踪精度对比

通过与其他算法比较观察文中算法的适用性。假设算法1中采用Singer模型，σa=0.1，α=1/20。算法2中采用文献[14]的Sine Wave模型，σa=0.1，α=1/18。算法3为本文算法，σω=10-8,σa=103,σϑ=10-4,α0=α1=10-3。算法4采用IMM(Singer + CA +CV)。进行100次蒙特卡洛仿真，得到结果如图12所示。

图12 系统输出误差Fig.12 Output error of system

图12为系统的输出误差，可看出在文中所设参数场景下，文中的双通道并行跟踪滤波算法具有更好的跟踪效果。

4 结 论

本文研究了临近空间高超声速滑翔弹的运动特性，分析了运动参数的变化规律，从角度域参数入手分别建立了目标横向和纵向的机动模型，提出了一种双通道并行跟踪算法，实现了三维跟踪。仿真对比表明，本文所提的算法具有较强的稳定性，具有较高的跟踪精度。