半直接配点法在航天器追逃问题求解中的应用

郝志伟，孙松涛，张秋华，谌 颖

(1. 哈尔滨工业大学航天科学与力学系，哈尔滨 150001； 2. 北京控制工程研究所，北京 100190)

0 引 言

两航天器追逃问题是一个对抗双方的控制策略选择问题，由于航天器动力学模型高维非线性且双方的对策目标相反，因此这样的问题求解十分困难。在航天器追逃中，追逐航天器希望选择控制策略使支付函数(payoff)最小，而逃逸航天器的期望则恰恰相反——选择控制策略使支付函数最大，该追逃过程可由微分对策理论描述。微分对策理论是研究两个或多个决策者的控制作用同时施加于由微分方程描述的运动系统时实现各自最优目标的对策过程的理论。该理论模型首先由Isaacs[1]提出，随着研究的深入，Berkovitz[2]和Friedman[3]给出了微分对策鞍点存在定理和最优控制策略存在的必要条件。

微分对策中各方策略最优的必要条件虽然已知[2-3]，但针对此必要条件的求解存在困难。因为此必要条件求解对应一个非线性两点边值问题(TPBVP)求解，而非线性TPBVP一般没有解析解，只能应用数值算法求解。目前，已存在的主要数值方法包括配点法[4]和多重打靶法[5]，它们各有优缺点。配点法将微分方程在配点处近似成代数方程，从而求解满足两点边值约束和代数方程约束的变量，进而求解两点边值问题。这种方法虽然收敛性好，但计算结果的精度不高，计算量大，且初值需要选择。多重打靶法通过数值积分公式在众多子区间上将一个微分方程离散成为代数方程，在任意子区间上求解一个初值问题，通过不断优化每一个区间上的初始值，最终满足两点边值条件。与配点法相比，多重打靶法的计算速度快、计算精度较高，但对初值非常敏感，因此收敛性差。航天器追逃问题一般对应复杂的高维非线性动力学模型，配点法虽对边值问题收敛性较强，但若随机给出初值，因模型复杂追逃问题数值解仍然不收敛。文献[6]提出了一种基于多目标遗传算法的初值选择方法，解决了航天器追逃问题中非线性TPBVP初值的选择问题，得到了收敛解。这种初值选择方法，对配点法和多重打靶法均有效。

本文采用半直接配点法求解航天器追逃问题，提出了一种新的数值求解追逃问题的思路，避免了非线性TPBVP求解，从而提高了数值求解追逃问题的效率。半直接法思想来源于Conway对导弹拦截问题的研究[7-8]，此方法通过一种变换将微分对策问题转化成一个最优控制问题，再将最优控制问题构造成一个非线性规划问题，然后应用序列二次规划算法(SQP)进行求解。文献[9]和[10]也利用了这种转化思想将微分对策问题转化为一个非线性规划问题求解，文献[10]还通过在目标函数中加入惩罚函数解决了状态量有约束的导弹追逃问题。但是，Conway的方法并不能证明半直接配点法求解微分对策问题得到的解一定是原问题的解。文献[11]证明了半直接配点法求解微分对策问题的等价性，为半直接配点法求解微分对策问题提供了理论依据。在求解两航天器追逃问题的过程中，通过半直接变换将微分对策问题转化为最优控制问题，通过Guass-Lobbato配点法数值求解此问题，提高了数值方法的收敛性和稳定性。

本文针对近地轨道附近时间固定的两航天器追逃问题，假设对抗双方均为连续小推力、对策时间较短、且瞬时状态信息完全已知，以距离为支付建立对策模型，给出了半直接配点法求解此追逃问题的数值方法。研究最终将给出追逃双方在对策条件下的最优策略，仿真算例表明半直接配点法为航天器追逃问题提供一种有效的求解方法。

1 航天器追逃问题建模

考虑近地轨道附近的两航天器P与E，O为P与E附近的一颗虚拟参考星。在以下内容中，P与E分别表示追逐航天器与逃逸航天器，两航天器的位置关系如图1所示，其中O-XYZ为参考坐标系，OX方向为地心连接参考星质心的连线方向，OY在参考星轨道平面内，延轨道速度方向，OZ轴与OX、OY轴构成右手坐标系，r(t)为参考星O点瞬时半径，xi(t)、yi(t)与zi(t)(i=P，E)分别表示两追逃航天器在参考坐标系X，Y和Z方向对应的分量。建立两航天器针对参考星的动力学方程如下：

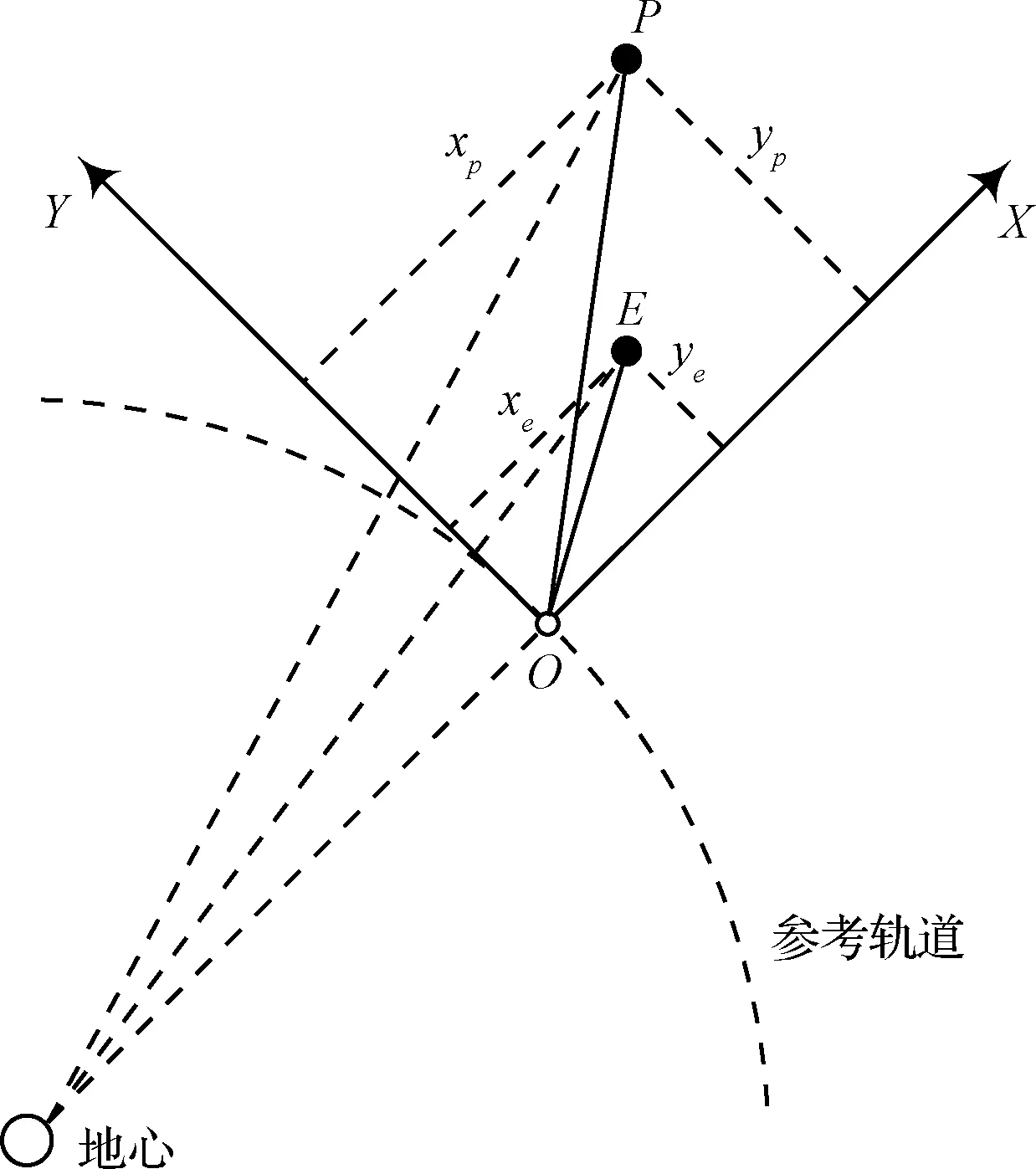
图1 两航天器对策的坐标示意图Fig.1 Coordinate frame sketch of pursuer and evader

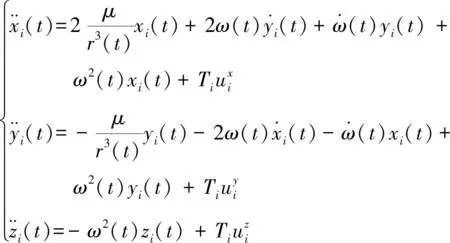
(1)

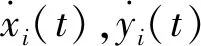
此航天器追逃问题的支付函数考虑为追逃对策结束时两航天器间距离：

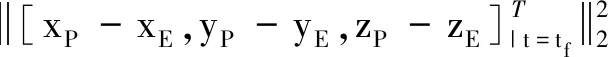
2 最优策略存在的必要条件

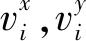
(2)

为了方便，令：

两航天器初值给定：

(3)

根据微分对策原理[1]，引入协态量λi(i=P,E)，

λi=[λ1i,λ2i,λ3i,λ4i,λ5i,λ6i]T,i=P,E

Hamilton方程H定义为：

(4)

根据最优策略存在的必要条件[2]，协态方程为：

(5)

相应的边值条件为：

(6)

[λ4P(t),λ5P(t),λ6P(t)]T

(7)

[λ4E(t),λ5E(t),λ6E(t)]T

(8)

显然，式(2)、最优策略必要条件(5)、(6)以及两航天器初值条件(3)组成了一个两点边值问题。一般的两点边值问题可由多重打靶法求解[8]。第3节将给出半直接法配点求解此上述两点边值问题的思路和过程。

3 半直接配点法

在半直接配点法中，将第2节最优策略必要条件得到的追逐或逃逸航天器的协态变量方程加入到状态方程中，同时将对应航天器的最优控制量表达式代入对应的状态方程并附上约束条件，将一个微分对策问题转化为一个最优控制问题。在求解中，只需求解一个对应的支付函数最大或最小问题即可，相应的等价性证明请参考文献[11]。具体求解步骤如下。

3.1 半直接转换

半直接配点法将微分对策问题转化为最优控制问题，这里将逃逸航天器E对应的协态变量λE加入到状态微分方程中。变换的方法简述如下，令：

(9)

由于已经将协态变量λE加入到系统方程(9)中，那么相应的终端约束方程Ψ定义为：

(10)

式中：

则变换后的支付函数仅为uP的函数：

(11)

显然，微分对策问题已被转化为一个最优控制问题(9)～(11)。对应追逐航天器P的半直接转化过程同上。接下来，将给出基于配点法求解转化后最优控制问题的方法。

3.2 半直接配点法的数值求解方法

考虑到计算精度，本文采用五阶Gauss-Lobbato配点法[12]求解上述最优问题。为说明此方法，不妨设式(9)对应的微分方程为

(12)

根据配点法，将时间区间[t0,tf]分为N个子区间(各个子区间的长度可以不相等)，每个子区间为[ti,ti+1](i=1,2,…N,t1=t0,tN+1=tf)，这样就确定了N+1个节点的位置，并得到初始的离散点。在每个子区间[ti,ti+1]上，应用多项式近似式(12)需先确定配点。由Gauss-Lobbato配点法[13]可知，除端点ti,ti+1外，其余三个配点tc1,tcm和tc2分别为：

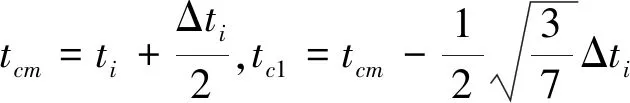
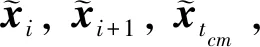
(13)

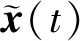
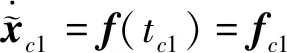
(14)

(15)

将式(14)与式(15)相加可得：

(16)

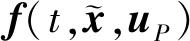
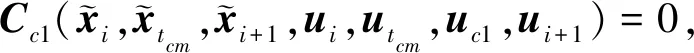
i=1,2,…,N

(17)

i=1,2,…,N

(18)

式中：符号N表示时间区间[t0,tf]上的子区间个数。

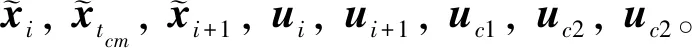
4 数值仿真结果

为说明半直接配点法求解航天器追逃问题的特点，将给出2个仿真算例。因为空间站和大量的卫星存在于地球低轨道，在仿真中参考星O轨道高度分别选为500 km和1000 km，追逃对策时间均为500 s。

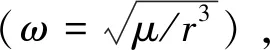
表1给出两个实例中追逐与逃逸航天器的初值，表2给出了实例中两航天的单位质量加速度，其中g=9.8×10-3km/s。

为了兼顾计算速度和精度，将时间区间划分为10个子区间进行仿真。由子区间的选择可知，需要求解的变量为483(2×10×18+(4×10+1)×3)个。

在数值仿真计算中，应用Gauss-Lobatto配点法并采用MATLAB语言编写的SNOPT求解器进行求解[13]。在仿真中，选用Core i7-4790K处理器、内存8 G的台式机进行数值计算。设约束精度和优化允许误差均为10-9。

在算例1中(参考星轨道高度500 km)，两航天器的轨迹和最优控制量变化曲线如图2所示。图2(a)～图2(f)分别给出了追逐航天器P与逃逸航天器E在固定时间500 s内X,Y和Z方向的位置与速度变化轨迹。追逐航天器P的最优控制量随时间变化曲线如图2(g)所示，逃逸航天器E的最优控制量随时间变化曲线如图2(h)所示。由图2可知，通过半直接配点法可获得航天器追逃问题收敛的解，图2(a)～图2(c)显示追逐航天器P零距离追上逃逸航天器E。在仿真算例1中，数值计算的约束误差为1.7532×10-11，计算时间为14.13 s。

在算例2中(参考星轨道高度1000 km)，两航天器的轨迹和最优控制量变化曲线如图3所示。与算例1相同，图3(a)～图3(f)分别给出了追逐航天器P与逃逸航天器E在固定时间500 s内X,Y和Z方向的位置与速度变化轨迹。追逐航天器P与逃逸航天器E的最优控制量随时间变化曲线如图3(g)和图3(h)所示。由图3可知，通过半直接配点法可获得航天器追逃问题收敛的解，图3(a)～图3(c)显示追逐航天器依然可以零距离追上逃逸航天器。在仿真算例2中，数值计算的约束误差为2.3584×10-11，计算时间为16.39 s。

由表2可知，在上述两个算例中，追逐航天器P的最大单位质量加速度均比逃逸航天器E的最大单位质量加速度大，这是追逐航天器P可以零距离追上逃逸航天器E的主要原因。

5 结 论

本文采用半直接配点法求解了近地轨道附近的两航天器追逃问题，得到了收敛的数值解。半直接配点法将一个微分对策问题转化成了一个最优控制问题，应用Gauss-Lobbato五阶配点法并结合序列二次规划法，最终解决了一个非线性的数学规划问题。采用半直接配点法求解微分对策问题时，可以避免求解困难的两点边值问题。这种算法具有收敛性好，应用简单的特点。数值仿真实例说明了这种求解方法在解决航天器追逃问题上的有效性。

图2 算例1：追逐和逃逸航天器的轨迹和最优控制变量Fig.2 Test case 1: trajectories and optimal controls of pursuer and evader spacecraft

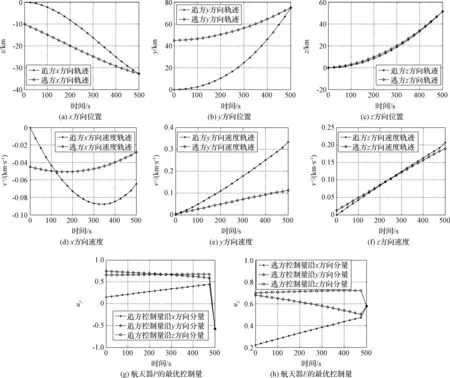
图3 算例2：追逐和逃逸航天器的轨迹和最优控制变量Fig.3 Test case 2: trajectories and optimal controls of pursuer and evader spacecraft

算例xP/kmyP/kmzp/kmvxP/(km·s-1)vyP/(km·s-1)vzp/(km·s-1)算例1000000算例2000000算例xE/kmyE/kmzE/kmvxE/(km·s-1)vyE/(km·s-1)vzE/(km·s-1)算例123.1430.08-0.011-0.033-0.0130.013算例2-10.1444.970-0.0450.00480.013

表2 两航天器的单位质量最大加速度Table 2 Max acceleration-to-mass of the pursuer and evader spacecraft