应用跟踪微分器的高超声速飞行器的反演控制
谭诗利,雷虎民,王鹏飞
(空军工程大学防空反导学院,西安 710051)
0 引 言
吸气式高超声速飞行器(Air-breathing hypersonic vehicle, AHV)因其广阔的军事和民用前景,已成为世界各大国在航空航天领域竞相追逐的一个重要目标。和传统飞行器相比,AHV具有复杂飞行环境、模型不确定性大、参数剧烈变化和耦合严重等特性,使得AHV飞行控制器的设计面临严峻挑战[1-2]。一方面,AHV飞行的临近空间存在非连续流体的现象,难以精确描述其气动特性,使得飞行器的建模存在误差。另一方面,轻质材料的使用使得飞行器的气动弹性效应显著,这种弹性形变也带来了模型的不确定性。如何避免模型不确定性对控制性能带来的不利影响是飞控系统设计中面临的关键问题之一。
面对不确定性控制问题,控制方法必须具备很强的鲁棒性。文献[3]采用H∞鲁棒控制方法设计了控制器,并提出了一种在线的同步逻辑更新算法求解Hamilton-Jacobi-Isaacs等式,有效地抑制了干扰和未建模动态的影响。但是上述鲁棒控制方法是基于小扰动线性化模型而开展控制器设计的,AHV的非线性实质和耦合被弱化。文献[4-5]分别运用径向基神经网络和模糊逻辑系统去在线逼近模型中的不确定项,虽然取得了较好的控制效果,但智能控制算法计算量较大且不利于工程实践。干扰观测器技术因其物理意义明确且工程适用性强,在不确定系统的控制领域被广泛应用。文献[6]利用超扭曲算法设计了超扭曲滑模干扰观测器,有效地获得了干扰项的信息,且观测的误差在有限时间内收敛,符合稳定性的要求。文献[7-9]基于滑模微分器设计了干扰观测器,对AHV的模型不确项进行平滑估计,实现了对参考轨迹的稳定跟踪,但滑模微分器的抖振现象难以避免。文献[10]采用扩展状态观测器(ESO)对模型中的不确定进行估计和补偿,所采用的ESO理论实质来源于韩京清等[11]提出的基于符号函数的跟踪微分器,抖振问题较突出。文献[12]中用于对干扰进行估计和补偿的非线性干扰观测器主要用于解决非匹配不确定性问题,形式较为复杂,使得控制器运算的时间复杂度增大。文献[13]在线性微分器和混合微分器等的基础上构造了一系列干扰观测器,并对比分析了对系统不确定性的估计能力。
上述分析表明,干扰观测器是解决不确定性控制问题的有效方法,又因为跟踪微分器(Tracking differentiator, TD)是干扰观测器设计的理论基础,故对跟踪微分器的发展现状进行论述。跟踪微分器的概念最早由韩京清等[11]提出,基于最速控制函数构造了具有纯开关形式的二阶跟踪微分器,但最速控制函数的Bang-Bang特性使得颤振现象十分明显。随后,文献[14-15]提出了兼具线性和非线性环节的全程快速跟踪微分器,提高了微分器的全程收敛速率,但在系统状态接近平衡点时,非光滑分数指数环节使跟踪输出信号明显颤振。赵鹏等[16]设计了一种改进的高稳快速跟踪微分器,在状态远离平衡点时,正奇数指数环节起主要作用,有利于微分器的快速收敛,在状态接近平衡点时,线性环节起主要作用,从而避免了跟踪输出颤振,但抑噪能力有限。近年来,研究热点集中在通过构造适当的加速度函数来提高跟踪微分器的响应速度、跟踪精度和抑噪能力[17-18]。为提高跟踪速率并避免颤振现象,要求构造的加速度函数在状态远离平衡点时具有非线性性质,状态接近平衡点时具有近似线性性质。
本文将研究高超声速飞行器在存在参数摄动和外部干扰等不确定下的控制器设计问题。首先,给出了高超声速飞行器的原理模型。然后,基于正切sigmoid函数和终端吸引子函数设计了跟踪微分器,通过扫频测试得到参数整定规则,并进行了对比仿真试验。随后,在反演框架下设计了具体的控制律,通过引入新设计的跟踪微分器,解决了传统反演控制的“微分项膨胀”问题,并在此基础上,设计了一种非线性干扰观测器,用以精确估计模型的不确定项,进一步提高控制精度。最后,通过仿真对所设计控制方法的有效性进行校验。
1 高超声速飞行器模型
国内外吸气式高超声速飞行器研究领域最常用的模型是美国空军研究实验室学者Bolender与Doman[19]提出的弹性体模型。以NASA研制的X-43 验证机为对象,基于机理推导的建模方法,建立了带有气推耦合和弹性形变影响的典型AHV模型。在以上研究基础上,Parker等[20]基于CFD仿真试验的建模方法,通过忽略模型中的一些弱耦合与慢动态,得到如下模型:
(1)

(2)
(3)

(4)
(5)
(6)
(7)
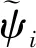
基于曲线拟合的思想,气动力、气动力矩及广义弹性力表示为虚拟控制量和控制量的非严格仿射形式[17]
(8)
2 跟踪微分器设计及分析
2.1 跟踪微分器设计
选取神经网络中常用的一种激励函数即正切函数作为加速度函数的基本形式,其表达式如下:
(9)
将上述函数在x=0处泰勒展开,得
tansig(x)=tansig(x)|x=0+tansig(x)′|x=0(x)+
tansig(x)″|x=0(x)2+…+Rn(x)=
x-2x3+O(x3)
(10)
式中:O(x3)表示x3的高阶项。
通过引入参数β,可以调节该函数近似线性区间的宽度,此时函数表达式为
(11)
分析式(11)所示的函数可知:当自变量趋近于0时,表现为良好的线性特性,且取值越小,近似线性区间宽度越宽;当自变量取值较大时,表现为饱和特性;且函数全局光滑。将函数作为跟踪微分器设计的基本函数,能够加快其全局收敛速率,使跟踪输出更加平滑,避免高频颤振,同时有效抑制系统高增益引起的峰值现象。此外,通过引入终端吸引子函数,可以有效增强跟踪微分器的抑噪能力,改善其滤波特性。根据以上分析,基于函数构造如式(12)所示系统,可得如下定理:
定理1. 对于给定系统
(12)
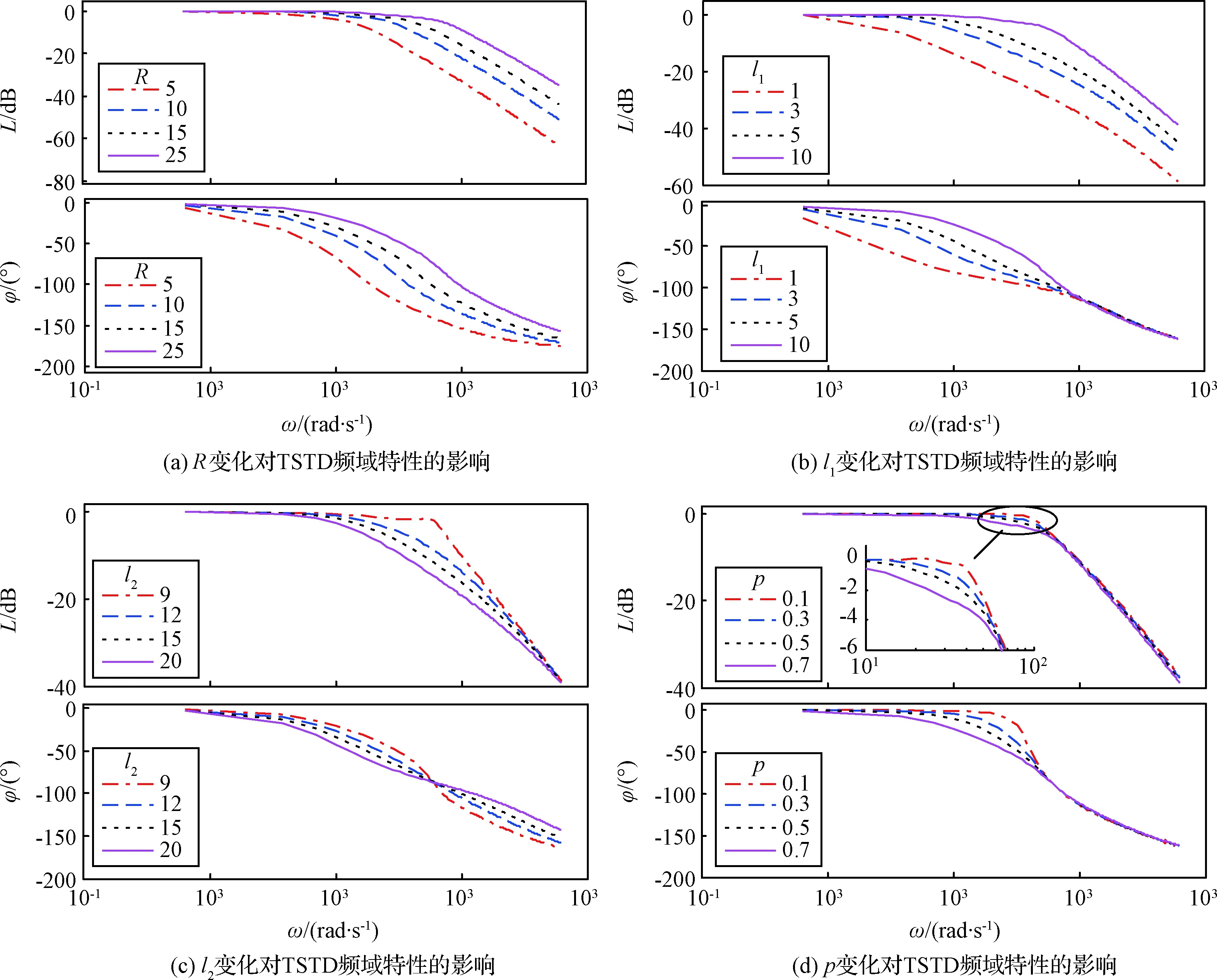
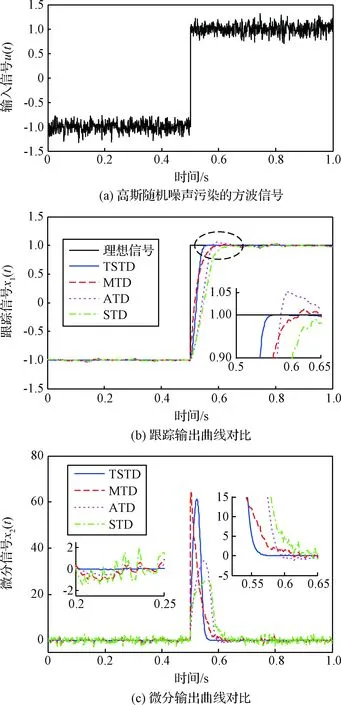
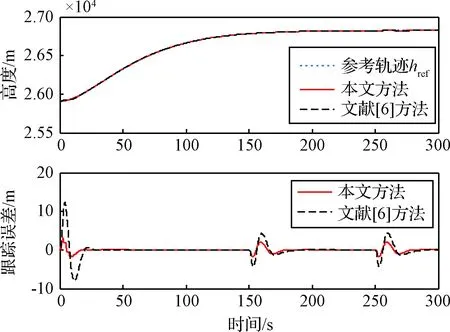
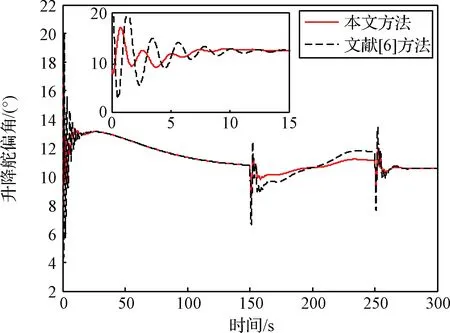
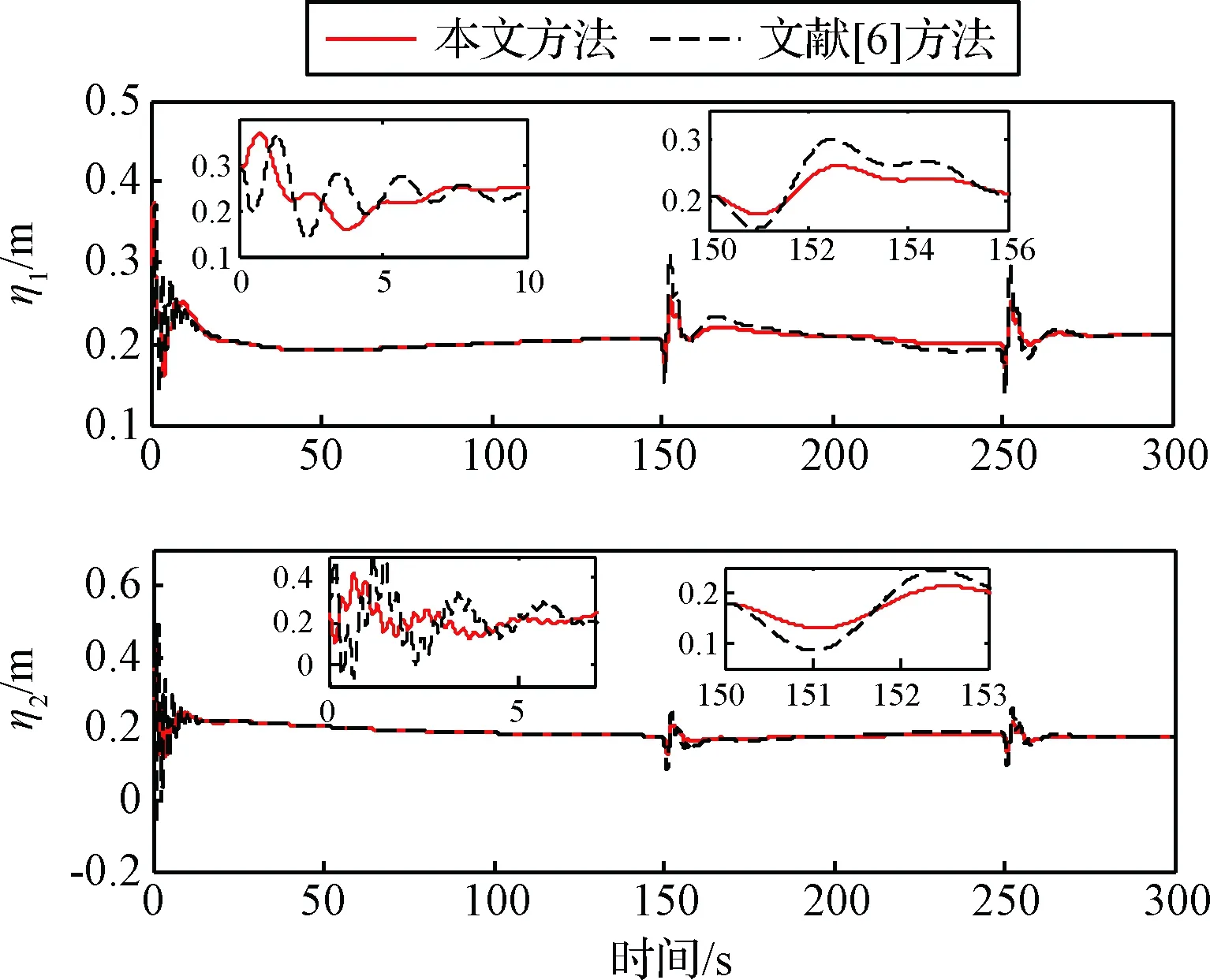
如果设计参数l1>0,l2>0,并且终端吸引子0 证.在包含(0,0)的领域内构造Lyapunov函数 (13) (14) 于是有 V(z1,z2)>0 (15) 将V(z1,z2)对时间t求导并结合系统(12),可得 (16) 当z2≠0时,均有z2tansig(z2)>0成立,因此可得 (17) 根据文献[17]中引理可知,系统(12)的解全局渐近稳定。 根据定理1,构造得到基于正切sigmoid函数的跟踪微分器(TSTD),如下所示 (18) 式中:u(t)为输入信号;设计参数R>0,l1>0,l2>0, 0 对于任意有界可积函数u(t)和任意正数T,系统(18)的解满足[13] (19) 根据定理1和上述的分析得到以下结论:所设计的跟踪微分器(TSTD)在理论上能够实现对输入信号的跟踪及微分信号的提取。 基于最小二乘法的扫频测试[24]能够较精确地获得所设计跟踪微分器的拟合Bode图,从而分析其开环频域特性。根据扫频测试结果分析TSTD的设计参数与响应速率、跟踪精度和噪声抑制能力的关系,从而得到微分器的参数整定规则,提升TSTD的工程实用性。本文利用扫频测试方法分析了TSTD的4个关键设计参数R,l1,l2和p的不同取值对微分器性能的影响,设计参数取值如表1所示。经过扫频测试,与之对应的幅频和相频曲线如图1所示。 表1 TSTD扫频测试参数取值Table 1 Values of TSTD’s design parameters 图1 设计参数变化对微分器的性能影响Fig.1 Effects of design parameters on frequency domain characteristics 分析图1(a)和图1(b),由对数幅频曲线可知,当设计参数R和l1增大时,系统的带宽频率增大。带宽越大,TSTD对输入信号的响应速率加快,跟踪输入信号的能力加强,但对高频噪声的抑制能力减弱。相频特性在截止频率以下相移很小,但在转折频率附近,相移很快降到-180°,这是一个较理想的相频特性。由图1(c)可知,当参数l2增大时,TSTD的滤波性能增强,但降低了对输入信号的响应速率和跟踪精度。图1(d)表明,增大终端吸引子参数p可以更好地抑制高频噪声,p越大,微分器的滤波性能越强,但同时也增大了微分器的跟踪时滞效应。 参数整定规则可归纳为:首先选取合适的β值,通常选择在5~20之间;其次选择p为较小值,以降低对噪声的敏感;随后,选择合适的R,然后微调l1和l2来调整跟踪和微分效果;最后通过调整p获取理想的跟踪、微分和噪声抑制效果。 为校验TSTD的跟踪与微分性能,进行仿真测试,并与高稳快速非线性—线性跟踪微分器(MTD)[16],反正切跟踪微分器(ATD)[17]和基于改进sigmoid函数的非线性跟踪微分器(STD)[18]进行对比。输入信号选取为高斯随机噪声污染的方波信号,仿真步长取为0.001 s。为保证比较的公平性,MTD,ATD和STD参数设置分别与文献[13-15]相同,TSTD的参数按照所总结的参数整定规则确定,并将速度因子R调整为相同值,各微分器的参数取值如表2所示。其跟踪和微分输出曲线如图2所示。 表2 四种微分器的仿真参数取值Table 2 Parameter values of four TDs 图2 4种微分器跟踪方波信号仿真图Fig.2 Simulation results of four TDs 观察图2(b)可知,在方波信号稳定在±1时间段,四种微分器滤波能力相当;在tj=0.5+jT/2,(j=0,1,…,n)时,TSTD实现了对方波信号快速跟踪,上升时间最短,且无超调,而ATD出现了严重的超调现象,MTD和ATD的跟踪响应速度较慢。从图2(c)可以看出,TSTD和MTD都得到了平滑的微分信号,响应速度较快,表现出良好的抑制噪声的能力;与STD相比,TSTD在抑制噪声方面明显占优,这是因为TSTD中的终端吸引子函数在一定程度上降低了噪声对微分信号的影响。仿真结果表明,TSTD能实现对方波信号的快速稳定跟踪,具备广义导数的求取能力,且能在一定程度上降低噪声的影响。 从式(1)~式(5)可以看出,由于燃料—空气比Φ直接影响推力,所以速度的变化主要受Φ控制;高度变化则主要由舵偏角δe控制,这是因为δe直接影响俯仰角速度Q,进而影响俯仰角θ与航迹角γ的变化,最后控制高度h的变化[21-22]。又由文献[23]可知,只要保证航迹角γ趋于航迹角指令γcmd,就能实现h对高度参考输入href的稳定跟踪,航迹角指令设计为 (20) 因此,AHV面向控制的模型可表示为 (21) 式中:dV,dγ和dQ表示各个通道上的包含参数摄动、外部干扰、气弹效应、信号转换误差和量测噪声等的总不确定项。 假设速度参考输入Vref,定义速度跟踪误差为 SV=V-Vref (22) 对式(22)求导并将式(21)代入,得 (23) (24) 式中:aV,1>0,aV,2>0,RV>0,βV>0和0 实际控制量Φ设计为 (25) 式中:kV,1>0和kV,2>0为设计参数。 定义航迹角跟踪误差为 Sγ=γ-γcmd (26) 对式(26)求导并将式(21)代入,得 (27) 同理,设计非线性干扰观测器如下 (28) 选取虚拟控制量为 (29) 式中:kγ,1>0和kγ,2>0为设计系数。 考虑引入新设计的TSTD对虚拟控制量θc求导,设θd为虚拟控制量θc经过TSTD微分后得到的信号,微分器设计如下 (30) 式中:R1,a11,a21,b1与β1均为待设计的参数。 定义俯仰角滑模面Sθ=θ-θd,则有 (31) 虚拟控制量Qc设计为 (32) 式中:kθ,1和kθ,2为设计参数。 类似地,设Qd为虚拟控制量Qc经过TSTD微分后得到的信号,微分器设计如下 (33) 式中:R2,a12,a22,b2与β2为待设计的参数。 定义俯仰角速率的滑模面为 SQ=Q-Qd (34) 对式(34)求导并将式(21)代入,得 (35) 同理,设计非线性干扰观测器如下 (36) 实际控制量δe设计为 δe= (37) 式中:kQ,1与kQ,2为设计参数。 定理2. 对于动力学模型(21),当采用控制律(25)和(37),非线性干扰观测器(24)、(28)和(36),微分器(30)和(33)时,则闭环系统全局渐近稳定。 证.定义dV,dγ和dQ的估计误差为 (38) 由式(19)可知,通过选择合适的设计参数可以保证估计误差有界,即 (39) 定义虚拟控制量的估计误差为 (40) 同样地,通过选择合适的微分器参数使得估计误差eθ和eQ有界,即 (41) 选取Lyapunov函数如下 W=WV+Wγ+Wθ+WQ (42) 式中: 对式(42)求导可得 (43) 由于 则有如下不等式成立 (44) 式中: 令控制器待设计的参数满足: (45) 并定义如下紧集 (46) 速度与高度参考输入分别由幅值为457.2 m/s和1219.2 m的阶跃信号经过阻尼比为0.95,自然频率为0.03 rad/s的二阶参考模型给出。模型中控制输入的幅值约束范围分别为:Φ∈[0.05,1.2],δe∈[-20°, 20°]。为验证所设计控制器的鲁棒性,考虑将所有气动参数分别加入±30%的摄动量,并在150 s≤t≤250 s时分别向动力学模型中加入下列扰动:dV0=sin(0.04πt) m/s,dQ0=0.2sin(0.04πt)(°)/s。为验证非线性干扰观测器对控制性能的提升,将本文所设计的控制器与文献[6]中的控制算法进行对比分析。 控制器参数取为:kV,1=1.8,kV,2=0.5,kh,1=2,kh,2=0.8,kγ,1=0.3,kγ,2=0.2,kθ,1=0.9,kθ,2=0.2,kQ,1=0.6,kQ,2=0.1;用于虚拟控制量求导的微分器参数取为:R1=R2=12,a11=a12=8,a21=a22=10,b1=b2=0.9,β1=β2=20;干扰观测器的参数取为:Ri=10,ai,1=8,ai,2=10,bi=0.9,βi=20, (i=V,γ,Q)。 注.控制器参数kV,1,kγ,1,kθ,1和kQ,1的取值范围需满足式(45)的约束条件,kV,2,kγ,2,kθ,2和kQ,2一般选取较小的数值来消除跟踪静差;虚拟控制量求导微分器的参数及干扰观测器的参数主要参考TSTD的参数整定规则进行选取。 图3 速度及其跟踪误差Fig.3 Velocity tracking and tracking error 图4 高度及其跟踪误差Fig.4 Altitude tracking and tracking error 图5 燃料—空气比Fig.5 Fuel equivalence ratio 图6 升降舵偏角Fig.6 Elevator angular deflection 图9 俯仰角速度Fig.9 Pitch rate tracking 图10 弹性状态量Fig.10 Responses of flexible states 对比分析图3和图4所示的跟踪误差曲线,本文设计的控制器在初始段时跟踪响应曲线的超调量明显减小且上升时间变短;在150 s≤t≤250 s遇到随机扰动时,本文设计的干扰观测器能够较大程度地减弱扰动对控制性能的影响。图5和图6表明,本文设计的控制器在控制输入上,初始段改善了抖振现象,外界扰动时需要的控制输入幅值变化更小且曲线更为平滑。由图7~图9可知,本文设计的控制器在跟踪航迹角、俯仰角和俯仰角速度拥有更高的跟踪精度。图10为弹性状态量的变化曲线,由于基于TSTD的干扰观测器能更实时、更精确地估计包含弹性状态在内的模型总不确定性,使得本文设计的控制器拥有更好的弹性抑制能力且弹性状态量能够在更短时间内趋于稳定状态。综上所述,本文设计的控制器在模型参数摄动和外界干扰存在的情况时,仍能保证闭环系统的稳定且具备较高的跟踪精度。 1)利用正切sigmoid函数和终端吸引子函数设计了跟踪微分器,通过扫频测试得到了参数整定规则,增强了工程实用性,并通过对比仿真说明,所设计跟踪微分器对方波信号的跟踪能力和微分能力较其它三种微分器具有更强的优势。 2)利用所设计的跟踪微分器实现了两个功能:一是构造了非线性干扰观测器对模型的不确定项进行估计,增强了所设计控制器的鲁棒性;二是利用所设计的跟踪微分器对虚拟控制量进行滤波处理,解决了传统反演控制的“微分项膨胀”问题。 3)针对存在参数摄动和外部干扰等不确定性的高超声速飞行器模型,基于反演框架完成了飞控系统的设计,并基于Lyapunov稳定性理论证明了整个闭环系统的稳定性,仿真结果表明所设计控制器完成了对参考指令的稳定跟踪并具备较高的跟踪精度。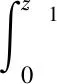

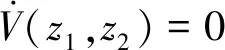

2.2 频率特性分析

2.3 对比仿真校验

3 控制器设计及稳定性证明
3.1 控制器设计
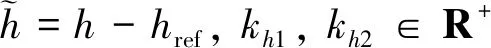
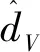

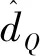
3.2 稳定性证明

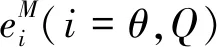
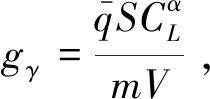
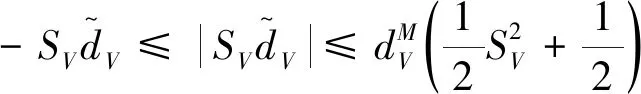
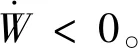
4 仿真试验
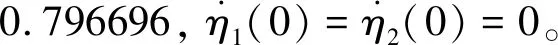


5 结 论

