浅谈数学建模在初中数学教学中的重要性

摘 要：《新数学课程標准》指出：“数学模型可以有效地描述自然现象和社会现象，课程目标让学生经历‘情境——建立模型——求解——解释与应用的基本过程，使学生学习数学的同时，在思维能力、情感、态度与价值观等多方面均得到发展。”本文根据自身的教学实践，简单谈谈数学建模在初中数学教学中的重要性。

关键词：数学建模;初中数学;重要性

近几年中考也加强了对以数学建模为中心应用题的考查。这些应用题，考查学生应用数学的能力。但学生在这些题上的得分率往往很低，原因之一就是学生缺乏数学建模能力和意识。因此，在初中数学教学过程中加强建模教学、渗透建模思想是非常必要的。

一、 初中数学建模常见方法

初中数学中常见的建模方法有：对现实生活中普遍存在的等量关系（不等关系），建立方程模型（不等式模型）;对现实生活中普遍存在的变量关系，建立函数模型;涉及测量建筑物的距离、高度、拦水坝的建造、航海触礁安全等问题，需要建立三角模型……

二、 初中数学建模基本步骤

（一） 分析问题

首先要认真审题。了解问题的实际背景，对问题进行化简抽象，构造出相应的数学模型。

（二） 抽象假设

根据问题的特征和目的，用精确的数学语言来描述。

（三） 建立模型

要根据实际问题的特征，在假设的基础上，建立相应的数学模型结构。

（四） 模型求解

利用所构建的数学模型，对所有参数作出计算。

（五） 模型分析

对所得的结果进行数学上的分析。

（六） 模型检验

把结果与实际情况进行比较，检验模型的合理性、准确性、和适用性。对计算结果进行验证和解释。

三、 初中数学建模案例分析

（一） 方程模型方程（组）模型

方程模型方程（组）模型是研究现实生活数量关系的数学模型之一，诸如打折销售、分期付款、储蓄利息、增长率、工程问题、行程问题等问题，都可以抽象成方程（组）模型，通过列方程（组）加以解决。

【例】 某工程队准备修建一条长1200m的道路，由于采用新的施工方式，实际每天修建道路的速度比原计划快20%，结果提前2天完成任务。若设原计划每天修建道路xm，则根据题意可列方程为。

分析：本题考查的是分式方程的应用。设原计划每天修建道路xm，则实际每天修建道路为（1+20%）xm，由题意提前2天完成任务，列出方程即可。即1200x-1200（1+20%）x=2。

（二） 函数模型

函数模型也是研究现实生活数量关系的数学模型之一，现实生活中的很多实际问题，诸如用料造价、合理决策、最佳投资、最大利润、最小成本、方案最优化等问题，都可建立函数模型求解。

【例】 某企业设计了一款工艺品，每件的成本是50元，为了合理定价，投放市场进行试销。据市场调查，销售单价是100元时，每天的销售量是50件，而销售单价每降低1元，每天就可多售出5件，但要求销售单价不得低于成本。（1）求出每天的销售利润y（元）与销售单价x（元）之间的函数关系式;（2）求出销售单价为多少元时，每天的销售利润最大？最大利润是多少？（3）如果该企业要使每天的销售利润不低于4000元，且每天的总成本不超过7000元，那么销售单价应控制在什么范围内？（每天的总成本=每件的成本×每天的销售量）

分析：（1）根据“利润=（售价-成本）×销售量”可列出函数关系式;（2）把（1）中的二次函数解析式一般形式转化为顶点式形式，再利用二次函数图象的性质进行解答;（3）把y=4000代入函数解析式，求得相应的x值;然后由“每天的总成本不超过7000元”列出关于x的不等式50（-5x+550）≤7000，通过解不等式来求得x的取值范围。

（三） 三角建模

三角函数作为刻画现实世界的一种常见数学模型，例如测量建筑物的高度、距离，航海，拦水坝的建造与相关的计算等问题，需要在具体情境中建立三角模型，转为三角函数问题。

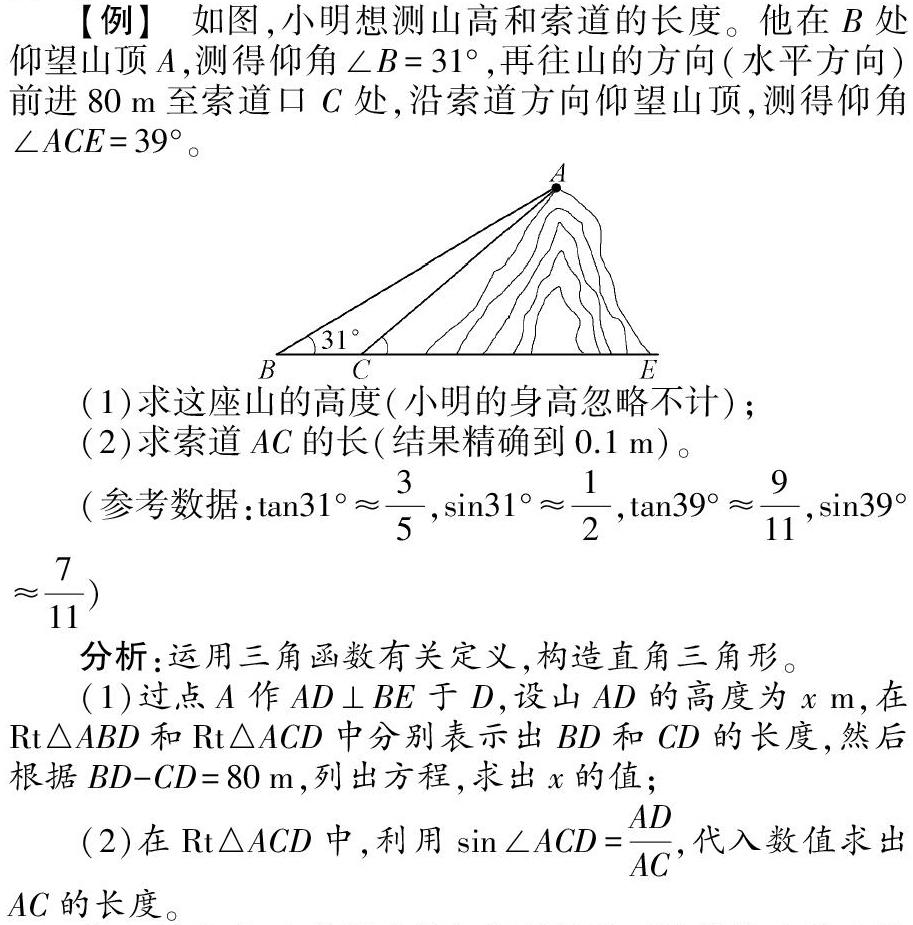
【例】 如图，小明想测山高和索道的长度。他在B处仰望山顶A，测得仰角∠B=31°，再往山的方向（水平方向）前进80m至索道口C处，沿索道方向仰望山顶，测得仰角∠ACE=39°。

（1）求这座山的高度（小明的身高忽略不计）;

（2）求索道AC的长（结果精确到0.1m）。

（参考数据：tan31°≈35，sin31°≈12，tan39°≈911，sin39°≈711）

分析：运用三角函数有关定义，构造直角三角形。

（1）过点A作AD⊥BE于D，设山AD的高度为xm，在Rt△ABD和Rt△ACD中分别表示出BD和CD的长度，然后根据BD-CD=80m，列出方程，求出x的值;

（2）在Rt△ACD中，利用sin∠ACD=ADAC，代入数值求出AC的长度。

综上所述，初中数学建模问题关键是要培养学生的建模能力，用数学方法和数学知识解决实际生活问题，这需要教师在了解学生的基础上，用恰当、正确的方法对学生加以指导和培养，是学生具备数学建模意识，从而解决数学问题及生活问题。

参考文献：

[1]展青岗.谈数学建模在初中数学教学中的重要性[J].华夏教师，2015（1）：45.

[2]叶雪琴.数学建模在初中数学教学中的渗透和培养[J].新课程：教育学术版，2009（5）：240.

[3]游莉.浅谈初中数学建模的重要性[J].科学咨询，2016（22）：126-128.

作者简介：

张爱华，山东省青岛市，山东省青岛莱西市实验中学。