三角形的最小覆盖圆一定是其外接圆吗

谢维勇

(四川省眉山中学校 620010)

在平面几何中，我们将能完全覆盖某平面图形且面积最小的圆称为该平面图形的最小覆盖圆.例如，线段AB的最小覆盖圆就是以AB为直径的圆.能完全覆盖住三角形的最小圆，叫做三角形的最小覆盖圆.

在学习完圆的方程后，经常遇见如下问题：

若一个三角形三边所在直线方程分别为x+2y-5=0,y-2=0,x+y-4=0，求能够覆盖此三角形且面积最小的圆的方程.

对于这类问题，多数同学通过简单的分析，会认为三角形的外接圆就是所求圆，然后给出如下解法.

解直线x+2y-5=0,y-2=0,x+y-4=0的交点为A(1,2),B(2,2),C(3,1),能够覆盖三角形ABC且面积最小的圆是△ABC的外接圆

设△ABC的外接圆的方程为x2+y2+Dx+Ey+F=0

将点A(1,2),B(2,2),C(3,1)分别代入方程得：

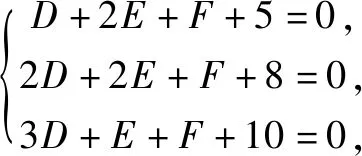
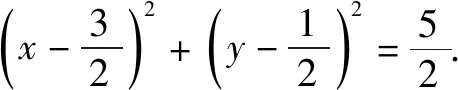
辨析所求圆要覆盖△ABC，则三个顶点均在圆上或圆内.若三个顶点都在圆内，则圆肯定不是面积最小的；若只有一个顶点在圆上，则圆面积一定可继续减小；若恰好有两个点在圆上，则这两点连线必然是圆的弦，欲使圆面积最小，则这两点连线恰好是圆的直径，且剩下的顶点需在圆内；若三个顶点都在圆上，则所求圆即为三角形的外接圆.

此题中，显然以AB,BC为直径的圆均不能包含剩下的顶点，以AC为直径的圆的方程为

那么，△ABC的最小覆盖圆就不可能是三角形的外接圆吗？如果不是，什么情况下才是三角形的外接圆呢？

根据上例的分析，只需考虑恰好有两点在圆上，剩余点在圆内和三点都在圆上两种情况.

如图是以AB为直径的圆O，若点C在圆O内，则连接BC并延长交圆O于点D,连接AD,则∠BCA>∠BDA=90°

若点C在圆O上，连接BC，AC,则∠BCA=90°;

若点C在圆O外，连接BC交圆O于点D,连接AD,则∠BCA<∠BDA=90°.

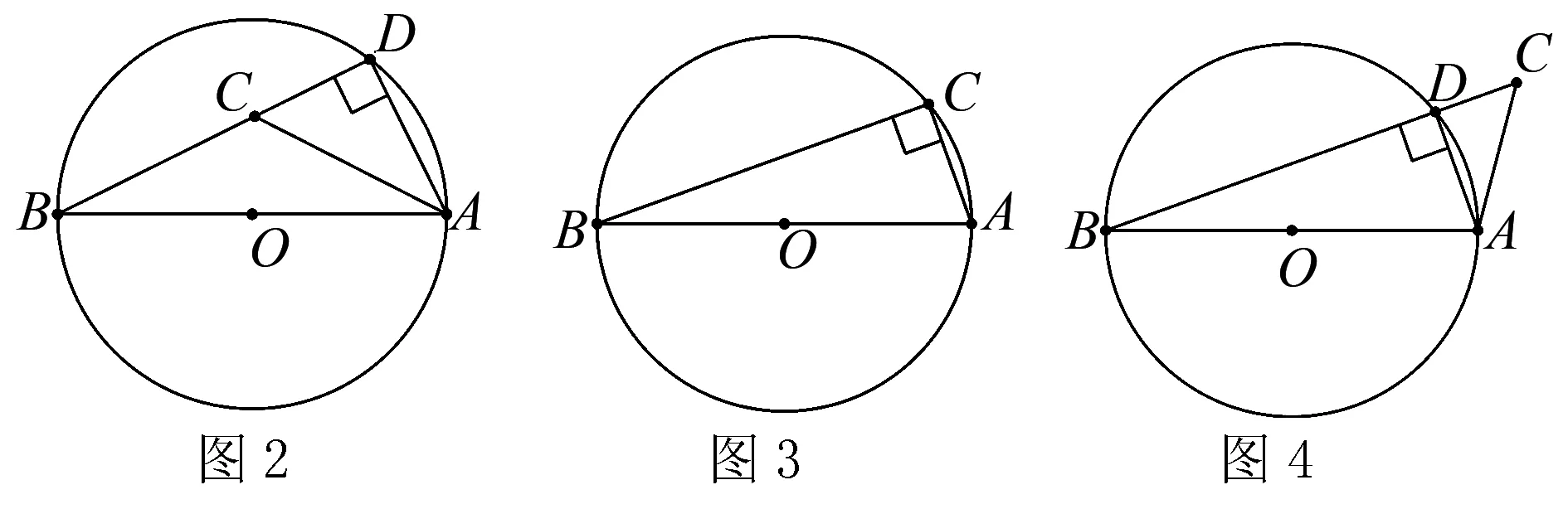
由上讨论可知：

当△ABC为锐角三角形时，任意边为直径的圆均不能覆盖整个三角形；

当△ABC为直角三角形时，只有以斜边为直径的圆刚好覆盖整个三角形，此圆即为三角形的外接圆；

当△ABC为钝角三角形时， 钝角所对边为直径的圆可以覆盖整个三角形，此圆的面积比三角形外接圆的面积小.

证明：设任意覆盖△ABC的⊙O的直径为d.

(1)当△ABC为直角或钝角三角形时,设△ABC最长的边为AC,线段AC为⊙O的弦或在圆及其内部,故d≥AC,而以AC为直径的圆一定覆盖了△ABC,因此以AC为直径的圆就是△ABC的最小覆盖圆.

(2)当△ABC为锐角三角形时, 如图,设直线AB与⊙O交于点D,E,直线EC与⊙O交于点E,F,不妨假定CF≤DA,过F作FG∥AC交直线AB于点G，则FG≥AC.

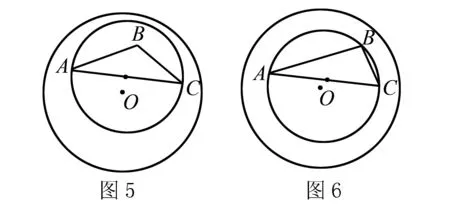
而∠DGF=∠DAC=180°-∠BAC>90°.

DF≥FG≥AC,又0°<∠AEC≤∠ABC<90°,

sin∠AEC≤sin∠ABC.

显然△ABC的外接圆覆盖了△ABC.

因此，△ABC的外接圆就是△ABC的最小覆盖圆.

综上，当△ABC为锐角或直角三角形时，能够覆盖三角形且面积最小的圆是三角形的外接圆；当△ABC为钝角三角形时，能够覆盖三角形且面积最小的圆是以最长边为直径的圆.