解析“鸡兔同笼”问题中存在的“惯性假设思想”

范 敏

(安徽省铜陵市爱国小学 244000)

“鸡兔同笼”问题是我国民间广为流传的数学趣题，最早出现在《孙子算经》中.是具备趣味性、挑战性及培养学生思维能力、逻辑能力的典型题型.常见的解法有：列表法、假设法、图示法、解方程法、金鸡独立法、抬脚法、砍脚法、安脚法、面积法.

案例呈现

例1鸡兔同笼，有5个头，14只脚，问鸡、兔各几只？

师：请同学们读一读，你从题里知道了几个条件？分别是什么？笼子里有多少只鸡和兔，我们一起来猜一猜好吗？

师：如果遇到数目大的时候，这种方法行吗？怎么办呢？(过渡到假设法)

生：假设全是鸡：

5×2=10(只)……如果把兔全当成鸡一共就有10只脚.

14-10=4(只)……每只兔就少了2只脚，4只脚是少算了兔的脚数.

4-2=2(只)……1只兔当成1只鸡就要少算2只脚.

4÷2=2(只) ……那把多少只兔当成鸡算就会少4条腿呢？就看4里面有几个2就是把几只兔当成了鸡来算，所以4÷2=2就是兔的只数.

师：除了假设全是鸡还可以怎么假设？

生：假设全是兔……

在执教”鸡兔同笼”问题时，老师们常常运用猜测和列表，初步感知发现形成规律，进而过渡到假设全是鸡或兔的情况，在老师提出让学生假设时，学生马上能给出假设全是鸡或兔的情况.笔者认为这是教师主观的“惯性假设思想”.首先学生不了解什么是假设法，他可以怎样假设，其次是不理解为什么选择假设全部都是鸡或兔.

策略呈现 例1鸡兔同笼，有5个头，14只脚，问鸡、兔各几只？

师：笼子里有多少只鸡和兔，我们一起来猜一猜好吗？

生1：可能有1只鸡4只兔.

……

生5：可能有5只鸡0只兔.

师：咱们可以将刚才猜测的不同情况列出表格.

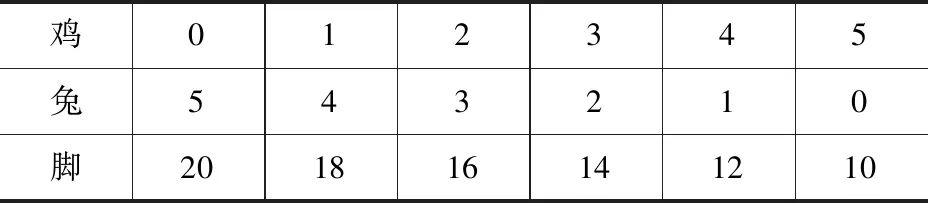
鸡012345兔543210脚201816141210

师：你有什么发现么？谁猜对了？

生：我发现×××猜得很准确：3只鸡2只兔刚好14只脚.

师：他是不是每次都能猜对呢？

生：不能每次都能猜到准确答案.

师：仔细观察表格你还有什么发现吗？

生1：我发现鸡的只数越多总脚数就越少，反之兔的只数越总脚数就越多.

生2：鸡和兔的总头数都是不变的.

生3：从左往右看每增加一只鸡，减少一只兔，总脚就减少2只.从右往左看每减少1只鸡，增加1只兔，总脚数就增加2.

师：你的发现真了不起.根据你的发现前面猜错的同学可以补救调整得出正确结果么？

生4：哦，我知道了.刚才我猜的是4只鸡1只兔，总脚数比实际脚数少2只.那我就可通过减少1只鸡，增加1只兔总脚数就会增加2.就能得出3只鸡2只兔共14只脚.

师：能听懂么？觉得他这种调整的思路怎么样？

生5：我觉得非常好，这个方法我也会了.我刚才猜的是1只鸡4只兔，总脚数多了4只.我可以增加2只鸡，减少2只兔子.总脚数就减少4只.得出正确结果是：3只鸡2只兔.

师：看来这个方法很不错.你们能根据这种调整的思路列出算式么？

生1：假设1只鸡，4只兔

2×1+4×4=18(只) 18-14=4(只) 4÷2=2(只)

1+2=3(只鸡) 4-2=2(只兔)

生2：假设2只鸡，3只兔

2×2+3×4=16(只) 16-14=2(只) 2÷2=1(只)

2+1=3(只鸡) 3-1=2(只兔)

生3：假设4只鸡，1只兔

2×4+4×1=12(只) 14-12=2(只) 2÷2=1(只)

4-1=3(只鸡) 1+1=2(只兔)

生4：假设全是鸡

2×5=10(只) 14-10=4(只)

4÷2=2(只兔) 5-2=3(只鸡)

生5：假设全是兔

4×5=20(只) 20-14=6(只)

6÷2=3(只鸡) 5-3=2(只兔)

师：比较一下这几种不同的假设，你有什么发现么？

生1：这些都是没有猜对答案，通过调整后得出结果的.

生2：我发现假设全是鸡或兔的这2种情况在计算时更容易理解计算起来也更方便.……

苏联教育家赞可夫说过:凡是儿童自己能够理解和感受的一切，都应当让他们自己去理解和感受.

教师首先引导学生从列表法观察发现蕴含的规律，让学生在这一过程中体会到：根据表实际的总脚数与自己猜想的总脚数差，来调整数据，对假设法的探究起到了铺垫作用，进而让学生大胆尝试采用各种可能性进行假设发现每一种可能性均可通过假设—计算—推理—解答得出正确结果.最后让学生观察对比不同假设方案进而得出假设都是鸡或都是兔这两种方案计算起来会更简便算式也更容易理解，优化了解题策略.从引导认识到优化假设方案循序渐进，水到渠成.

虽然本节课研究的内容有些抽象，但这些抽象的东西其实都来源于现实生活.因此，真正的知识是来源于感性经验的，我们的数学教学不能脱离学生的经验，简单枯燥的讲解已经远远不能满足现在学生的需要.所以数学课越来越注重加入动手操作、小组讨论、合作学习等活动，希望通过活动让学生获得更多数学经验.直接的活动经验可以通过猜想、绘画、交流探讨中获得，而间接的经验可以在构建数学模型中所获得，思考的活动经验需要通过分析、归纳等方法获得数学经验，如预测结果、探究成因等等.