对一道中考压轴题的溯源、多解与思考

杭 静 陈德前

(1.江苏省兴化市板桥初级中学 225700;2.江苏省兴化市教育局教研室 225700))

一、试题呈现

如图1，在平面直角坐标系xOy中，,边长为a(a为大于0的常数)的正方形ABCD的对角线AC、BD相交于点P，顶点A在x轴正半轴上运动，顶点B在y轴正半轴上运动(x轴的正半轴、y轴的正半轴都不包含原点O)，顶点C、D都在第一象限．(1)当∠BAO=45°时，求点P的坐标；(2)求证：无论点A在x轴正半轴上、点B在y轴正半轴上怎样运动，点P都在∠AOB的平分线上；(3)设点P到x轴的距离为h，试确定h的取值范围，并说明理由．

二、设计溯源

看到这道试题，我们不禁联想到苏科版教材七年级下册第149页数学实验室的内容和八年级上册第59页的第11题：画∠AOB=90°，并画∠AOB的平分线OC.

(1)把三角尺的直角顶点落在OC的任意一点P上，使三角尺的两条直角边分别于OA、OB相交于点E、F(如图2①)，度量PE、PF的长度，这两条线段线段吗？

(2)把三角尺绕点P旋转(如图2②)，PE与PF相等吗？证明你的结论．

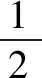
三、多解呈现

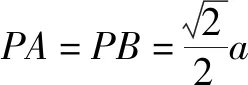
(2)解法1：∵ 四边形ABCD是正方形，∴∠APB=90°，PA=PB．取AB的中点M，连接PM、OM，如图3.∵∠APB=∠AOB=90°，∴BM=AM=OM=PM，即A、O、B、P四点共圆，∴∠AOP=∠BOP，即OP平分∠AOB.

解法2：∵ 四边形ABCD是正方形，∴∠APB=90°，PA=PB．取AB的中点M，连接PM、OM，如图3，∵∠APB=∠AOB=90°，∴BM=AM=OM=PM，即A、O、B、P四点共圆，∴∠AOP=∠ABP=45°；同理∠BOP=45°，即OP平分∠AOB.

解法3：如图4，过点P作PE⊥OP，交x轴于点E.∵∠APB=∠AOB=90°，∴∠PBO+∠PAO=180°，而∠PAE+∠PAO=180°，∴∠PBO=∠PAE；由∠APB=∠OPE=90°，有∠OPB=∠APE；又PB=PA，∴△PBO≌△PAE，∴PO=PE，得∠POA=45°，∴OP平分∠AOB.

解法4:如图4，在OA的延长线上截取AE=BO，连接PE.∵∠APB=∠AOB=90°，∴∠PBO+∠PAO=180°，而∠PAE+∠PAO=180°，∴∠PBO=∠PAE；又PB=PA，∴△PBO≌△PAE，∴PO=PE，∠BPO=∠APE，∴∠OPE=90°，∠POA=45°，∴OP平分∠AOB.

解法5：∵ 四边形ABCD是正方形，∴∠APB=90°，PA=PB．将△PBO绕点P旋转90°到△PAE的 位置.∵∠APB=∠AOB=90°，∴∠PBO+∠PAO=180°，∴∠PAE+∠PAO=180°，∴点E在OA的延长线上，如图4，∴∠OPE=∠APB=90°．

山东省济宁市鱼台县王庙镇棉花种植面积有5万多亩，郝集村的刘磊今年种植了不少亩棉花，为了准确把握棉花各生育期生长特点及需肥规律，验证云天化复合肥在棉花种植中所展现的效果是否能满足植物生长所需的营养，待试验结束后对照试验用肥量、用肥成本、用肥肥效、棉花产量等综合因素下，云天化复合肥同其他厂家的肥料的优缺对照，云天化工作人员选择了刘磊家的棉花作为对照试验的样本，想通过田间试验，总结出一套适合棉花生长全程营养解决方案，为云天化复合肥做好技术服务指导，提高云天化复合肥的影响力。

由PO=PE，有∠POA=45°，∴OP平分∠AOB.

解法7：如图6，过点D作DE⊥x轴，垂足为E，交射线OP于点F.同证法6可知△ABO≌△DAE，∴BO=AE，OA=DE；再由BO与EF平行，有∠POB=∠F，又∠OPB=∠FOD，∴△PBO≌△PDF，∴BO=DF，∴OE=OA+AE=DE+OB=DE+DF=EF，∴∠FOE=45°，∴OP平分∠AOB.

解法8：如图6，过点D作DE⊥x轴，垂足为E.同证法6可知△ABO≌△DAE，∴BO=AE；连接PE，∵∠APB=∠AOB=90°，∴∠PBO+∠PAO=180°，而∠PAE+∠PAO=180°，∴∠PBO=∠PAE；又PB=PA，∴△PBO≌△PAE，∴PO=PE，∴∠BPO=∠APE，∴∠OPE=90°，∠POA=45°，∴OP平分∠AOB.

解法9：如图7，过点P作PE⊥x轴，过点B作BF⊥PE，垂足分别为E、F.可证△PEA≌△BFP，得PE=BF，又BF=OE，∴PE=OE，得∠POE=45°，∴OP平分∠AOB.

解法10：如图8，过点D作DE⊥x轴，垂足为E，过点C作CF⊥y轴，垂足为F，DE与FC交于点H.易知四边形OEFH是矩形；∵AB=AD，∠ABO=∠DAE，∴Rt△ABO≌Rt△DAE，∴BO=AE，AO=DE，同理，Rt△ABO≌Rt△BCF，∴OA=BF，∴OE=OF，∴四边形OEFH是正方形，∴DH=BD.连接PH，可证△PBO≌△PDH，∠BPO=∠DPH，∴O、P、H在同一直线上，∴OP平分∠AOB．

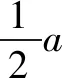
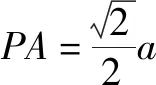
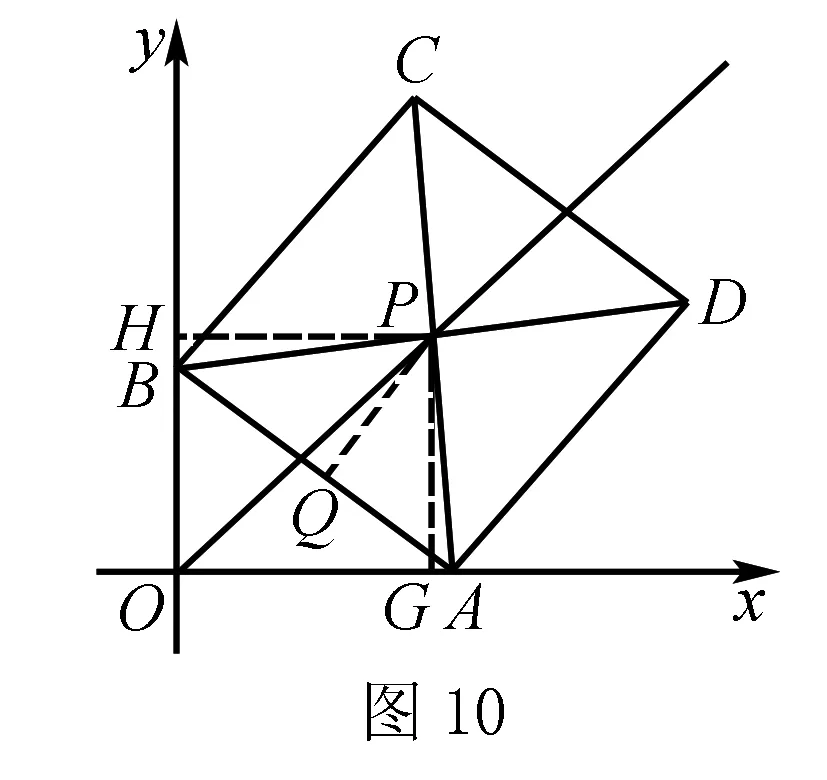
理由5：过P作PM⊥x轴于M, 如图11①.

四、教学思考

要想顺利地解决压轴题,在复习教学中，我们必须加强以下几方面的工作:

1.重基础.要重视知识的基础性、全面性，切实掌握基础知识、基本技能、基本思想方法,做到概念清晰无误,运算熟练准确,思路简捷有序.要构建完整的知识体系，让各种概念、定理、公式、常用结论及解题方法，都能在头脑中再现，象本题的求解中用到的点的坐标、特殊角的三角函数值、全等三角形的判定与性质、特殊平行四边形的性质与判定、中位线定理、函数解析式的求法、面积法等都是初中阶段重要而基础的知识，务必要切实掌握，只有这样，才能在解题时得心应手，游刃有余.

2. 优思维.要优化思维品质，努力培养思维的深刻性、广阔性、灵活性、批判性.思维深刻、批判能力强的同学，解题时不会一有了解题思路就迫不及待地动笔解答，而是广开思路，寻找最优的解法.如在第(2)小题的解决过程中要从图形中去寻找有关信息，思考简便解法.这样做虽然分析问题的过程拉长了，但落笔做题的时间却大大缩短了，真正起到了事半功倍的效果.

3．提能力.要发展探究能力，掌握重要的思维方式.目前数学开放型试题的研究已成为中考数学命题的热点问题，如第(3)小题，研究开放探索型问题，给我们提供了自主探索的机会.要顺利解决开放探索型问题，就要关注数学能力的发展，掌握常用的思维方式，提高运用所学知识和技能分析问题与解决问题及获取信息的能力.要全身心的参与探究活动的全过程，在观察、实验的活动中，通过比较、分析、归纳、类比、抽象等思维活动，获取数学猜想再进行说理，创造性地解决有关开放探索型问题.