透过全等思想看中考题中的线段关系

宫庆军

(山东省淄博市博山中学 255200)

在历年的中考中经常出现三角形及隐形三角形(需添加辅助线)的问题，问题涉及到线段的关系，有位置关系和数量关系，此时考生能否顺利完成试题的关键是要有全等的思想和类比的思想，抓住这两点可能问题就会迎刃而解.下面就几个中考的题或者经典的题做论述.

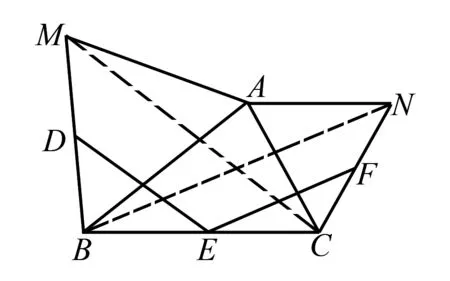
例1(经典)如图，已知△ABC是锐角三角形，分别以AB，AC为边向外侧作两个等边△ABM和△CAN．D，E，F分别是MB，BC，CN的中点，连结DE，FE，求证：DE=EF．

解题分析本题中多个中点会联想到中位线定理，进而作辅助线MC和BN，它们的关系就是DE和EF的关系，等边三角形中有相等的边和角自然想到△AMC和△ABN的全等问题，进而证得MC=BN，所求问题依据中位线定理自然解决了.具体过程不再赘述.

例2(淄博中考)(1)操作发现：如图①，小明画了一个等腰三角形ABC，其中AB=AC，在△ABC的外侧分别以AB，AC为腰作了两个等腰直角三角形ABD，ACE，分别取BD，CE，BC的中点M，N，G，连接GM，GN．小明发现了：线段GM与GN的数量关系是____；位置关系是____．

(2)类比思考：如图②，小明在此基础上进行了深入思考．把等腰三角形ABC换为一般的锐角三角形，其中AB>AC，其它条件不变，小明发现的上述结论还成立吗？请说明理由．

(3)深入研究：如图③，小明在(2)的基础上，又作了进一步的探究．向△ABC的内侧分别作等腰直角三角形ABD，ACE，其它条件不变，试判断△GMN的形状，并给与证明．

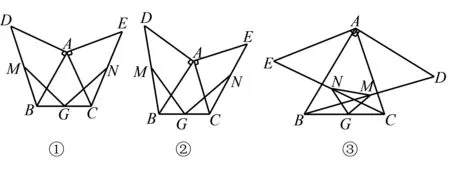
解题分析和例1比较它把外接等边三角形换成了等腰直角三角形，使问题变得复杂了，GM与GN的关系可能就不止是相等这么简单了，应该能想到是垂直关系，先猜测再去证明是关键.此类问题均是从一个三角形出发，向外作几何图形，从而产生问题，让学生作答，抓住全等三角形这个工具，同时体会类比思想的重要性.

∴MG=NG，MG⊥NG.故答案为：MG=NG，MG⊥NG.

(2)连接CD，BE，相交于H，同(1)的方法得MG=NG，MG⊥NG.

(3)连接EB，DC，延长线相交于H.

同(1)的方法得MG=NG.

同(1)的方法得△ABE≌△ADC，∴∠AEB=∠ACD，∴∠CEH+∠ECH=∠AEH-∠AEC+180°-∠ACD-∠ACE=∠ACD-45°+180°-∠ACD-45°=90°，∴∠DHE=90°，同(1)的方法得MG⊥NG．

例3(济南中考)如图1，在Rt△ABC中，∠ACB=90°，AC>BC，分别以AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG，连接EF、GM、ND，设△AEF、△BND、△CGM的面积分别为S1、S2、S3.

(1)猜想S1、S2、S3的大小关系,深入研究;

(2)请对(1)的猜想，任选一个关系进行证明；

(3)若将图1中的Rt△ABC改为图2中的任意△ABC，若S△ABC=5，求出S1+S2+S3的值；

(4)若将图2中的任意△ABC改为任意凸四边形ABCD，若S△AEG+S△CNK+S△IBH+S△DFM=a，四边形ABCD的面积为____.(直接用含a的代数式表示结果)

解题分析此题和淄博中考题类似，它外接的是正方形，内部图形无论怎么变化，它的解题思路不变，利用全等找出相等的线段关系，进而证得面积相等，不过它的线段相等更具有隐藏性，辅助线的作法稍微有点难度，更加考验考生的思维能力.具体思路如下：很容易得到S3=S△ABC.进一步猜想其它的两个三角形面积也等于S△ABC，此时需要证明它们的高或底边相等，延长FA至H作EH⊥AH，由△ABC≌△AEH得到EH=BC，进而得到S1=S△ABC，进而得到S1=S2=S3，用类比的思想就能解决后面的问题.

全等三角形的运用一直是数学的重要组成部分，它就像数学中的一个根源所在，许多问题皆由它而来，它涉及了几何中最重要的角和线段的关系.不仅在于它让学生学会了数学的几何证明方法，也让学生体会了数学中的转化思想.它具有很大的灵活性，也具有一定的难度，有时候找不到哪两个三角形全等，此时就要从三角形全等的性质入手，具体数学问题具体分析，体现了学生的各种综合能力.全等三角形知识是几何教学的中轴线，是基础，是代数和几何连接的纽带.