星载SAR图像几何校正影响要素分析

赵建辉田军锋左宪禹李 宁

(1.河南省大数据分析与处理重点实验室， 河南开封 475004； 2.河南大学计算机与信息工程学院， 河南开封 475004)

0 引言

随着SAR(Synthetic Aperture Radar)技术的发展，SAR图像在军事和国民建设中都发挥着日益重要的作用。但是，受地形的影响和斜视成像的原因，SAR图像总是存在不同程度的几何畸变，在应用之前需要作几何校正。目前，在星载SAR图像的几何校正中广泛使用距离-多普勒(Range Doppler，RD)模型，国内外的一些学者研究了该模型的近似解法[1-5]。

几何校正中可能的误差来源有卫星星历误差、系统成像参数误差、DEM(Digital Elevation Model)误差[6-7]，以及定位方程的误差[8]和解算误差。星历数据和系统成像参数由卫星公司提供，由SAR图像元数据直接给出，其误差没有办法通过算法进行弥补，需要其他数据(例如DEM或控制点)辅助修正[9-11]。因DEM产生的定位误差与DEM数据本身的精度和地形都有关，地形越平坦定位精度受其影响越小，反之越大。定位方程的解算中可能会产生较大误差的主要因素是卫星轨道的拟合和插值。

本文分析了RD定位模型的建立和几何校正中该模型的解算过程，探讨了影响定位精度的两个主要因素：高程、轨道的拟合与插值。目前能公开免费获取的高程数据并不少，但全球覆盖的不多，常见的有ASTGTM2[12]、SRTM4.1[13]和GMTED2010[14]，标称分辨率为30，90和250 m，从有关文献的比较来看，垂直精度依次升高。在我国东部平原，垂直精度也有类似的表现[15]。常用的卫星轨道拟合与插值方法是多项式直接法和拉格朗日法。本文以一景高分辨率TerraSAR-X图像的几何校正为基础，分析和验证了上述三种DEM和两种轨道插值算法对定位精度的影响。

1 R-D定位模型的建立及其解算

精确的SAR图像定位必须充分考虑SAR图像的成像原理和成像几何，并以此为基础建立定位模型，而实际定位精度又与模型的初始化数据和解算方法密切相关。

1.1 定位模型的建立

SAR图像的定位需要综合考虑成像原理和成像几何两方面的条件。

从成像原理上讲，SAR图像是基于地物的多普勒雷达回波信号成像。SAR对目标进行照射后，回波以目标为中心产生多普勒效应，可用等时延的同心圆和等多普勒频移的双曲线束来描述，如图1所示，图中T为地面目标。针对回波的这种特性，定位以多普勒中心频率为基准。当频移为零时，SAR刚好正对成像目标，便于成像几何的解算。

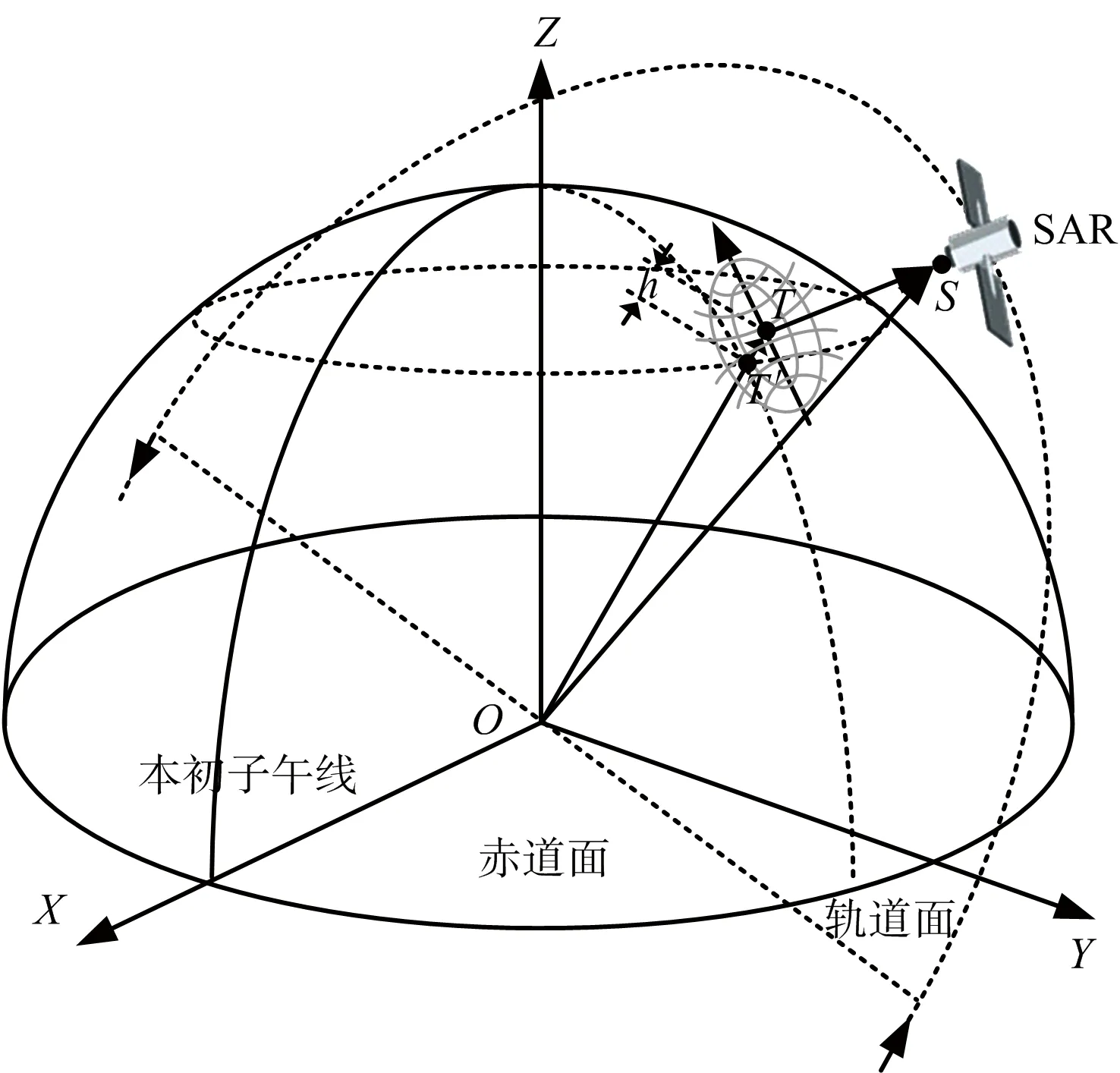
图1 SAR图像地理定位模型示意图

从成像几何来讲，SAR与地面目标、地心构成一个三角形。地理定位中常将地心放在一个地固坐标系的原点，如图1所示。图中O为地心，S表示SAR的位置。这时候S点的状态矢量(包括空间矢量PSO和速度矢量V)为已知条件，T到S的距离可根据回波时延计算得到，而T的位置可以用空间矢量PTO来描述。

有了上述条件，就能建立如下方程来表示在地固坐标系下上述矢量之间的关系。

(1)

式中，fd表示多普勒频率，λ表示SAR的波长，|PSO-PTO|就是卫星到地面目标点T的距离。

此外，还需要地球椭球方程来描述地面目标T的空间坐标参考。

(2)

式中，ra，rb分别表示地球椭球模型的长、短半轴长度，h表示地面高程。如图1所示，T′表示T点在参考椭球上的位置，h是二者之间的距离。

1.2 几何校正中定位模型的解算及其影响因素分析

定位模型解算的目标是T点的向量PTO，基本条件为SAR图像的成像几何，约束条件为零多普勒频移。因此，T点的定位过程可以描述为零多普勒条件下根据成像几何计算矢量PTO的过程。

几何校正采用间接定位方法，定位方程的解算步骤如下：

1) 定位模型线性化，求误差方程。

由于式(1)和式(2)并非线性方程，不能直接用于平差计算，可以对它们进行泰勒级数展开，取一次项组成误差方程，但这种方法计算量较大。更简单的方法是用牛顿迭代法直接逼近多普勒中心频率，其迭代公式如下：

Δfd=|fd(ti+Δti)-fdc|

(3)

(4)

式中,fdc为SAR多普勒中心频率，新一代SAR图像(如TerraSAR-X图像)已经作了归零化处理，无须计算。式(4)中，Δt的初值可以由经验值直接给定，可大可小(如10 ms)，对收敛速度并无影响。

对于老一代SAR图像fdc可用式(5)进行计算：

fdc=d0+d1(t-t0)+d2(t-t0)2+d3(t-t0)3

(5)

式中，变量t为当前快时间，参数t0，d0，d1，d2，d3由SAR图像元数据直接给出。

上述迭代公式在实际应用中收敛速度快，定位效率高。

2) 根据误差方程的解算需要获取初始化参数。

所有的初始化参数都可以从SAR图像元数据中直接提取。几何校正中需要从元数据中提取的主要信息有3大类，包括图像信息、时间信息和卫星星历信息。图像信息包括SAR图像的成像类型、行数、列数、行序、列序等，时间信息主要是方位向起止时间和距离向起止时间，卫星星历信息主要是距离矢量、速度矢量和时间向量。此外，还需要其他一些辅助信息，如坐标参考。

3) 逐像元求解空间坐标。

有了初始化参数之后就可以开始计算每个像元的空间坐标了。因为多普勒频率fd主要受时间的影响，所以计算的基本方法是以时间t为自变量，求解t时刻的fd与多普勒中心频率fdc之间的差值。在迭代中不断调整t，使差值减小。当差值小于某个阀值时，就可以认为该时刻的空间坐标达到要求的定位精度。

几何校正的基本流程如图2所示。

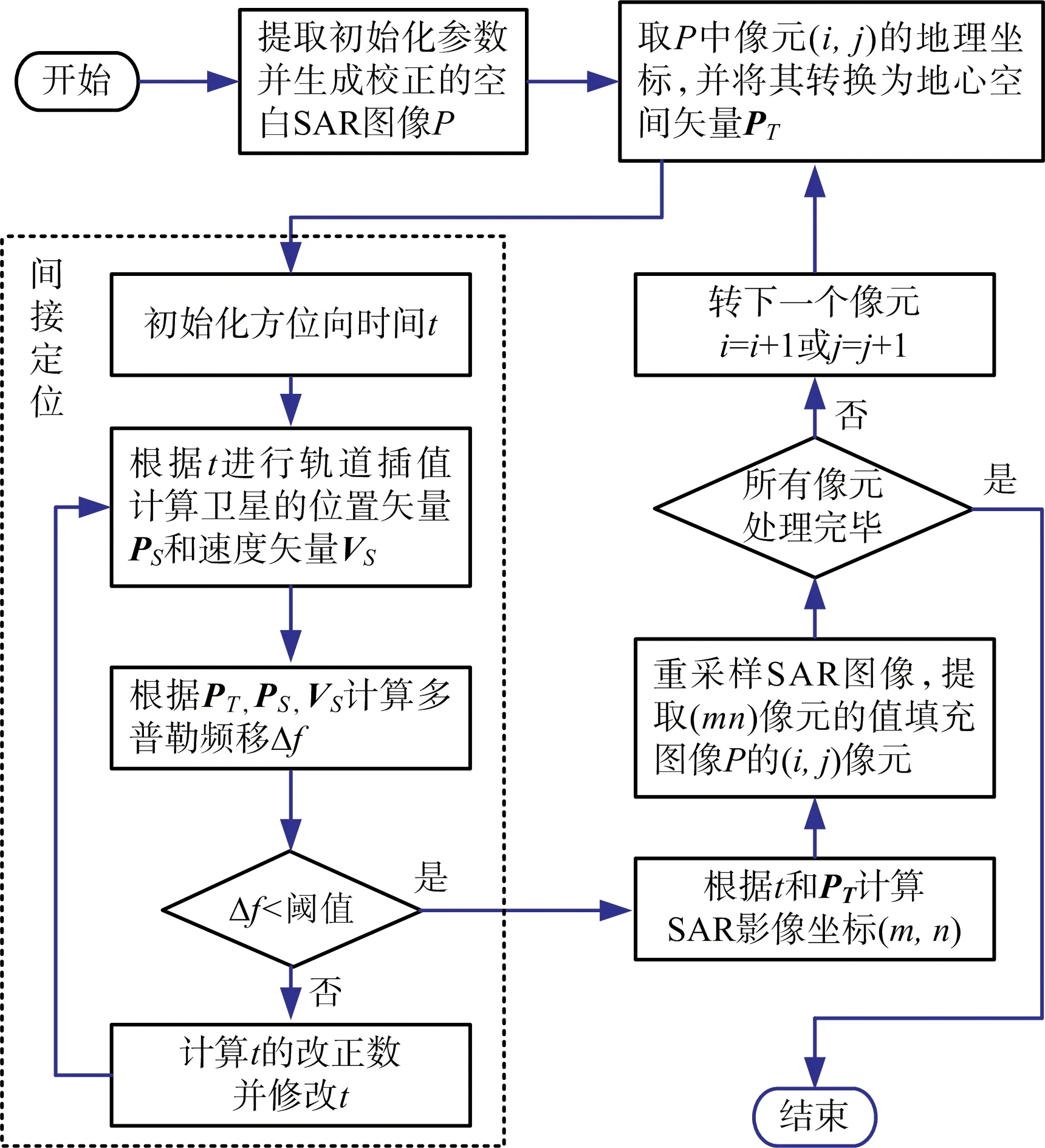
图2 SAR图像几何校正流程

图2中虚线框内为几何校正的关键步骤——间接定位。迭代的初始坐标对应的矢量PT由待定位像元的地理坐标计算出来，时间t的初值可在成像时间范围任意选定。对于每一时刻t，通过轨道插值计算出相应距离矢量PS和速度矢量VS。有了PT，PS，VS，就可以根据式(1)计算出fd。如果fd与fdc的差值小于阈值就结束迭代，否则根据相差一个Δt的两个fd的差值计算t的改正数，修正t后继续迭代。迭代结束后的PT就是所求像元的空间矢量。

4) 提取像元值，生成最终的校正图像。

根据迭代结束时的t和PT反解出原SAR图像的像元坐标，然后重采样获取像元值填充待校正SAR图像完成校正过程。

从整个校正过程来看，对定位精度有直接影响的是高程的精度、轨道的精度和轨道插值的精度。但在几何校正中，轨道的数据作为输入数据是以状态向量的形式由SAR图像直接给出的，定位模型本身无法对其进行修正。

对整个校正精度有影响的还有坐标变换和图像重采样，前者是地理坐标、空间坐标和像元坐标三者之间的转换，相对误差很小，后者常用的方法有最邻近、双线性和三次卷积法，第3种方法已经能够保证足够高的精度。

2 几何校正实验及其分析

本文使用了一幅SSC类型的TerraSAR-X高分辨率图像作为实验对象，原图及校正结果如图3所示。图像的成像模式为滑动聚束，成像时间为2015年6月17日，方位向分辨率为1.1 m，距离向分辨率为0.6 m，图像大小为6 143行11 100列。图像对应的地区为平原，元数据给出的全景图像平均高程为56.775 m。

图3 实验用的SAR图像

实验中我们从图像中选取了13个点(图3中用红色十字标出)，采用手持GPS(水平精度2 cm)测量了各点的精确位置。实验利用前述RD定位模型对影像进行了几何校正，并以此为基础分析和比较了3种DEM、不同参数的多项式直接插值算法和拉格朗日插值算法对定位精度的影响。

1) 基于3种DEM的定位实验及分析

对于高程来说，分辨率越高越好，最好是不低于SAR图像的分辨率，这样才能保证每个像元对应的高程精度。因为定位中各像元的高程多是通过重采样获得，采样点距离被采样点越近准确率越高，反之越低。显然，地形起伏越大，这种影响越显著，反之影响越小。

实验使用的DEM数据有ASTGTM2，SRTM4.1和GMTED2010，它们的分辨率与实验用的SAR图像相差很大。但是，考虑到实验图像中的地形较平坦，它们也具有一定的适用性。3种DEM在该图像区域的平均高程分别为55.335，55.669和55.416 m，略小于图像元数据给出的值，理论上对定位精度有1～2个像元的影响。表1给出了采用这3种高程数据的定位实验结果。

从SAR图像成像的几何原理来看，对定位精度影响最大的应该是DEM的垂直精度。垂直精度越高，定位精度就越高，反之越低。而分辨率对重采样的精度影响大，从而间接影响垂直精度。图1的定位结果符合这一预期。

表1 方位向和距离向定位残差统计表单位：像元

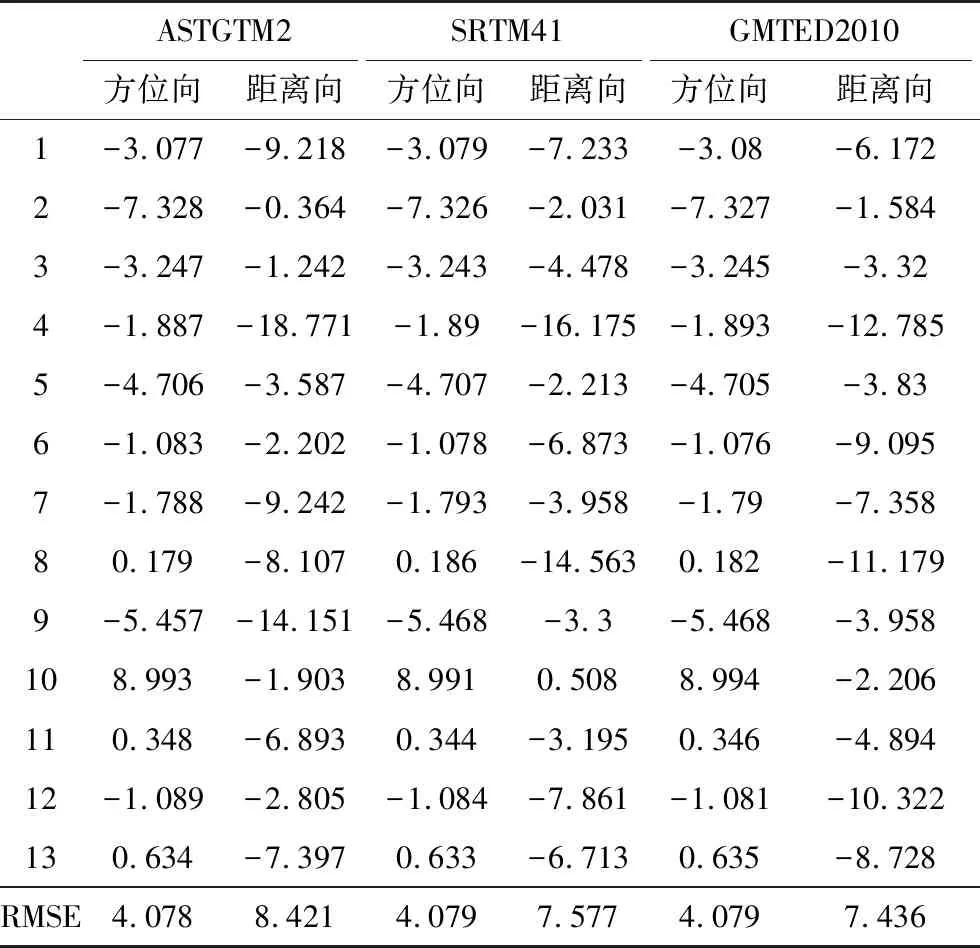
ASTGTM2SRTM41GMTED2010方位向距离向方位向距离向方位向距离向1-3.077-9.218-3.079-7.233-3.08-6.1722-7.328-0.364-7.326-2.031-7.327-1.5843-3.247-1.242-3.243-4.478-3.245-3.324-1.887-18.771-1.89-16.175-1.893-12.7855-4.706-3.587-4.707-2.213-4.705-3.836-1.083-2.202-1.078-6.873-1.076-9.0957-1.788-9.242-1.793-3.958-1.79-7.35880.179-8.1070.186-14.5630.182-11.1799-5.457-14.151-5.468-3.3-5.468-3.958108.993-1.9038.9910.5088.994-2.206110.348-6.8930.344-3.1950.346-4.89412-1.089-2.805-1.084-7.861-1.081-10.322130.634-7.3970.633-6.7130.635-8.728RMSE4.0788.4214.0797.5774.0797.436

从残差的均方根误差RMSE来看，定位精度达到了预期目标。方位向定位精度大致为4个像元(约5.5 m)，距离向定位精度大致为8个像元(约5 m)，这个结果符合所用图像的高分辨率与地形较平坦这两个特点。

方位向和距离向的定位精度受DEM精度的影响差异也符合SAR图像的成像原理。方位向定位精度主要受时间影响，所以定位结果几乎不受DEM分辨率和精度的影响。而距离向定位精度受成像几何的影响大，因此受DEM的精度影响大。3种DEM中，GMTED2010垂直精度最高、SRTM4.1次之、ASTGTM2最差，表1的定位结果与这些差异一致。但是，因为地区较平坦和GMTED2010分辨率低的缘故，这种优势并不明显。

此外，从定位的整体结果来看，无论是方位向还是距离向，多数为负值。但是，理论上这些值的正负应该是随机的，这表明定位存在一定的系统误差。进一步的精度提升需要其他辅助手段，例如使用角反射器测定精确的地面控制点。

2) 基于不同的轨道插值方法的定位实验及分析

对于轨道插值来说，常用的有多项式直接法和拉格朗日法。前者还有幂次的区别，幂次越高，精度越高，但计算速度会随之降低。显然，只要精度能够满足应用需要，没有必要过度追求高幂次。

从理论上讲，轨道插值的精度对图像的方位向和距离向都有影响。但是，实验表明不同插值法之间在方位向和距离向的差异小。本文采用了平面定位精度来比较它们的影响，测试了多项式直接法和拉格朗日法，前者又测试了二、三、四次幂的情况，各种方法的定位残差如表2所示。

表2 平面定位残差统计表 m

定位结果大致符合预期，幂次越低，误差越大。从残差的均方根误差RMSE来看，只有二次多项式插值法出现了较大误差，不适合用在定位中。三次、四次多项式直接法和拉格朗日法均取得了较好的结果。但是，三次多项式直接法在x方向上的精度还有提升空间。拉格朗日法的精度高，只有四次多项式直接法与之接近。事实上，实验还进一步测试了五次和六次多项式直接法(表2中未列出)，但x和y方向上精度都不再继续提升，而是围绕某个值上下波动，显然精度无法再继续提升。

从整体来看，四次多项式和拉格朗日插值法都适合用在SAR图像的高精度定位中。但前者的计算效率比后者高得多，更适合用在工程中。

此外，与方位向误差和距离向误差类似，三、四次多项式和拉格朗日法的x向偏差均为负值，y向几乎均为正值，同样表明定位存在一定的系统误差。

3 结束语

在基于RD模型的几何校正中，影响校正精度的因素有很多，本文着重研究了高程和轨道拟合与插值方法对定位精度的影响。从实验的结果来看，高程的垂直精度和分辨率对定位精度都有重要影响。在平原地区，影响定位精度的主要是垂直精度。这与同行们的研究结果一致，而分辨率则对起伏较大的地形定位精度影响大。显然，对于ASTGTM2，SRTM4.1和GMTED2010这3种高程来讲，实际应用中选择哪一种取决于地形和精度的要求，平坦的地区GMTED2010就足够了，而地形起伏较大的地区，可根据实测结果选择ASTGTM2或SRTM4.1。卫星轨道的插值中，四次多项式直接法已经能够满足快速高精度定位的需要。进一步的精度提升还需要其他辅助手段，比如使用类似角反射器的工具测定精确的地面控制点，以此对定位结果进行整体修正。

此外，论文中的方法还在Radarsat-2图像和COSMO-SkyMed图像的几何校正中进行了验证，也取得了良好的效果。相对来说，Radarsat-2图像的轨道精度最低，卫星状态矢量也只提供了5个，使用RD模型进行定位时残差并不稳定，即使用元数据中给出的控制点也一样，不过官方提供了一种有理多项式模型来弥补这一缺陷。实际应用中使用RD模型高精度定位还需要其他数据对轨道进行修正。而TerraSAR-X和COSMO-SkyMed的轨道精度都能满足直接使用RD模型高精度定位的要求，而且提供了更多的卫星状态向量，前者提供了12个，后者提供了15个。