基于LS迭代熵值穿墙雷达墙体杂波抑制

李家强，卢宝宝1，徐小敏1，陈金立

(1.南京信息工程大学电子与信息工程学院， 江苏南京 210044；2.南京信息工程大学气象灾害预报预警与评估协同创新中心， 江苏南京 210044)

0 引言

穿墙成像雷达产生于20世纪末，是一类重要无损侦测技术。它利用了电磁波低频大波长的穿透特性，对非透明墙体后的隐藏目标进行侦测。通过结合超宽带 (Ultra Wideband，UWB)与合成孔径雷达(Synthetic Aperture Radar，SAR) 两项技术，穿墙成像雷达可以获得目标精确的高分辨率图像[1-2]。

在穿墙成像雷达探测并对墙体后目标成像过程中，因为墙体对电磁波作用的影响，信号在墙体障碍物内的传播过程中能量发生迅速衰减，而且目标本身仅具有微弱的电磁散射特性，使得所需回波信号往往会被淹没在墙体杂波中。因此，如何有效滤除非目标回波，提高目标信号检测率成为墙体后目标成像的至关重要因素[3-4]。为解决这一难题，国内外学者开展了相关研究，并获得了一些研究成果[5]。Yoon 等[6]提出一种空域滤波的方法，该方法以墙体回波空间特征具有不变性为前提，把回波空间谱看成中心为零的一种正弦脉冲，利用目标回波空间频谱扩展的特性，根据墙体与目标之间具有的空间差异采用合适方法滤除掉杂波信号，其优点是不需任何的先验信息便能达到滤除非目标信号的效果。然而现实环境具有一定的复杂性，这会导致墙体与目标的空间谱在零频附近的公共频带展宽，无法达到理想滤除杂波效果。背景相消算法[7]能够较好地滤除墙体及墙体后的杂波，但该类方法是需要目标以及墙体背景环境等先验信息，在某些情况下却是无法获得足够的墙体后环境信息。另外，奇异值算法(SVD)具有低复杂度、计算量小的特点，但如果目标介电常数小，就会达不到理想的杂波抑制效果。为了更好抑制墙体杂波，Raffaele等研究者提出了利用基于熵值信息杂波抑制算法[8]，其主要思想是比较目标与墙体障碍物之间具有不同的熵值，采用合适阈值进行杂波滤除。较之前面所述算法，基于熵值算法并不需墙体参数及环境背景先验信息。然而，该算法在得到熵值之前，需要计算回波数据的概率空间。在目标信号微弱的情况下，部分天线阵元接收到的回波幅值可能接近于零值，因而导致无法准确的滤除杂波，且对目标回波信号造成一定的损耗，最终影响输出信杂比以及成像的效果。

针对上面所述问题，本文提出了一种基于熵值的拉普拉斯平滑处理的墙体杂波抑制方法。首先将回波信号离散化，然后在计算回波数据概率空间时，对其进行拉普拉斯平滑处理，得到平滑后的数据熵值，设置合适门限值，得到初次滤出杂波的数据。为了提高输出信杂比，再进行一次矩阵升维处理，进一步滤除杂波。最后对处理后的数据进行后向投影成像。

1 穿墙成像雷达实验场景与回波信号建模

1.1 实验场景建模

穿墙雷达实验建模如图1所示。将目标设置为理想电导球体，位置在两墙体之间，直径设置为2r，圆心与前墙体之间距离设置为h1，前墙与后墙的厚度为h2，相对介电常数设置为εr，天线与墙体之间的距离设置为h3，天线扫描次数为N。天线发射脉冲信号Ricker子波，其表达式如下：

图1 穿墙雷达实验模型

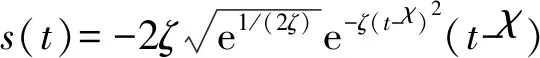
(1)

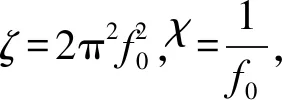
1.2 接收回波信号模型

天线接收的回波信号模型表示如下[8]：

e(t)=ea(t)+ew(t)+et(t)

(2)

式中，ea(t)为天线耦合波信号，ew(t)为前墙体与后墙体的反射信号，et(t)为所要得到的目标回波信号。为了实现高输出信杂比，这里就需要滤除掉墙体杂波ew(t)。

2 杂波抑制与滤除算法

2.1 滤除直达波信号

穿墙雷达在扫描过程中，不可避免接收到各种杂波信号。尤其是直达波信号ea(t)，此回波信号幅值有时甚至超过目标信号。为了不影响本文算法抑制墙体杂波的效果。首先对直达波采用基于格林函数的滤波法进行滤除。由于获得的仿真数据为时域数据，在时域中，入射波与格林函数关系为

(3)

(4)

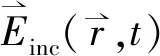
2.2 拉普拉斯平滑原理

拉普拉斯平滑(Laplace Smoothing，LS)又被称为加1平滑[9]，该平滑方法主要为了解决零概率事件问题。所谓零概率事件，就是在计算实例中的概率时，如果某个分量在训练集中从没出现过，会导致整个实例的概率计算结果为0。针对本文信号分类问题就是当某一处的离散信源数值等于或趋近于零时，在计算此处概率时会得到零值，由此判断此处信源数值概率为零，进而影响到整体回波信号熵值的计算，这显然是不合理的。拉普拉斯平滑基本原理如下：

对于一个随机变量z，k次实验后的观测结果为{z(1),z(2),z(3),…,z(k)}，极大似然估计按式(5)计算：

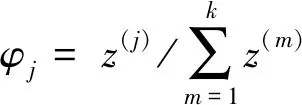
(5)

式中，z(j)为信号回波幅度，φj代表在阵元j处接收到回波为z(j)的概率，k为天线扫描次数N。使用拉普拉斯平滑后，式(5)变为

(6)

即在分母上加的数值为天线阵元总数N，分子上加1。

2.3 墙体杂波信号抑制

经过去直达波处理之后，回波信号式子变为

(7)

aij(i=1,2,…,M,j=1,2,…,N)为第j处天线阵元的第i个采样点接收到的回波信号强度。

下面即对墙体杂波ew(t)进行抑制和滤除。在回波数据离散情况下，aij的概率P(aij)可通过式(8)计算：

(8)

由于回波信号较弱，所以部分接收天线阵元接收到回波信号的强度很低，甚至近似为零值，导致上述公式无法计算。因此，可通过拉普拉斯平滑处理，即概率计算公式(8)改为

(9)

信息熵由式(10)计算：

(10)

由于墙体回波的不确定度相对于目标信号的不确定度较大，因此墙体回波熵值较大，而目标信号熵值较小，这样可以通过设定门限来消除墙体杂波，即

eZ1(i,j)=Z1(i)·e1(i,j)

(11)

式中，eZ1(i,j)为处理后的回波数据，而Z1(i)可定义为

(12)

式中，logN为门限值，因子β调节门限大小，取值范围(0,1)。为了提高信杂比增量，可进一步扩大熵值门限，即将eZ1(i,j)中的零值去掉，重新得到矩阵eZ2(i,j)，维数大小为M1*N(M1≪M)，该矩阵仅包含少量墙体杂波，大部分为目标数据。为了不改变原有回波数据具有的性质，即墙体杂波不确定性远大于目标不确定性，又能提高门限值，采用下列公式：

e2(i,j)=e1(i,j)*eZ2(i,j)′

(13)

获得数据为e2(i,j)，矩阵大小变为M*M1。其中eZ2(i,j)′代表矩阵eZ2(i,j)转置。对矩阵e2(i,j)进行迭代熵值处理得到e3(i,j)，具体过程如下：

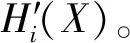
e3(i,j)=Z2(i)·e2(i,j)

(14)

其中,Z2(i)可定义为

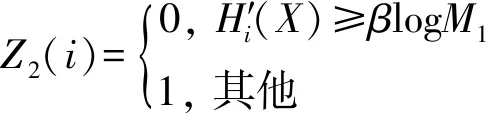
(15)

式中，logM1为更新的门限值，调节因子β取值范围不变。

经过上述处理后，对处理后的数据e3进行后向投影成像，算法优劣指标选用目标杂波比(Target-to-Clutter Ratio，TCR)，本文采用目标杂波比定义公式如下[10]：

(16)

式中,At为目标区域，Ac为杂波区域，Nt为目标区域对应成像点数，Nc为杂波区域对应的成像点数目，I(n)为某点像素值。

3 实验与结果分析

由图1所示建立实验模型，本文仿真软件选择基于时域有限差分方法GprMax2D/3D[11-13],获得的回波数据进行算法处理实验，具体操作过程如下：

选取天线放置在离前墙体h3=0.05 m处，然后进行平行于墙体等间距N次扫描，扫描范围是0.1～2.1 m。假设墙体设为均匀介质，前墙体与后墙体厚度均设为h2=0.2 m，其相对介电常数为εr=6.4。选取目标为理想电导球体，直径设为0.2 m，球心到前墙体的距离为h1=1.0 m，发射信号为Ricker子波。

选取阵元扫描次数N=26，每次采样点数为2 036，从回波数据分析中可知在阵元12处，采样点从939到951与982到1 000处的采样点回波振幅极其微弱，接近于零。在进行本文算法之前必须先进行直达波的滤除。仿真软件GprMax得到的原始二维回波数据如图2(a)所示，滤除直达波后的数据如图2(b)所示。

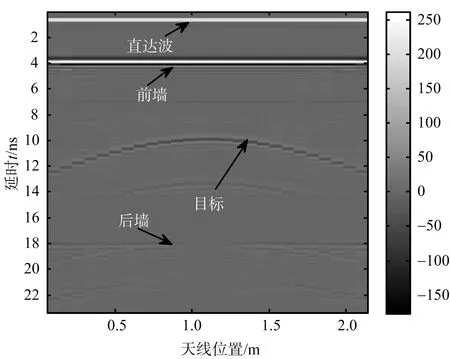
(a) 直达波滤除前

(b) 直达波滤除后图2 基于格林函数的直达波滤除

经过上述处理之后，得到去直达波的回波数据。为了获取较高输出信杂比，采用文献[8]的算法以及本文所提算法分别对墙体杂波进行处理，得到去墙体杂波的数据。然后利用后向投影算法分别进行成像，成像结果如图3和图4所示。其中图3为经过去直达波后的BP成像，从图中能够看出前墙体与后墙体依然存在，此时信杂比为-4.21 dB。

图3 原始信号成像

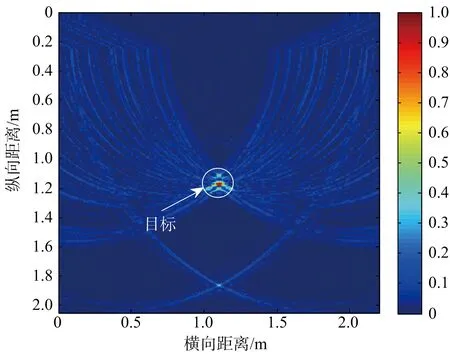
(a) 熵值法杂波抑制后成像

(b) LS法处理后成像

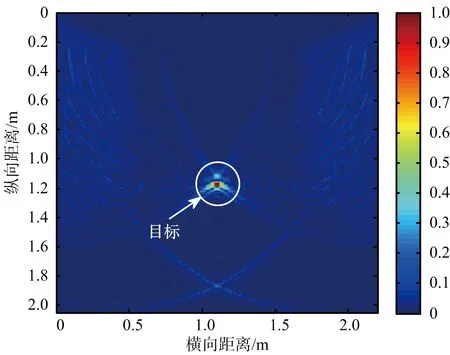
(c) LS迭代法处理后成像图4 杂波抑制后的图像

图4(a)为算法[8]基于熵值处理后的成像结果，从图中可以看出墙体杂波得到一定的抑制，但是信杂比并不理想，主要是由于部分采样点回波幅值较低，部分甚至接近于零，在计算概率空间时误判信源数值概率为零，得不到该处采样点正确的熵值，导致此采样点被误判为杂波数据并被滤除掉，继而影响算法的正确性。图4(b)为在计算概率时采用了拉普拉斯平滑处理，然后再进行熵值处理之后得到的成像结果，由图看出，成像效果明显提高，通过平滑处理，有效目标数据得到保留，而非目标信号得到滤除。信杂比改善量ΔTCR也得到了一定的提高，约为15.59 dB。图4(c)为采用拉普拉斯平滑处理并经过一次迭代处理的成像结果，输出信杂比大大得到了提升。为了验证本文所提算法的有效性，分别对基于熵值法、拉普拉斯平滑处理与拉普拉斯平滑迭代处理后的输出信杂比改善量的比较，如表1所示。

从表中可以看出基于熵值的杂波抑制方法，信杂比增量为13.31 dB，处理后的杂波比变为9.10。回波数据经过拉普拉斯平滑处理后，输出信杂比提高了2.28 dB。而本文所提算法在较低输入信杂比(-8.26 dB)时，输出信杂比增量改善了6.45 dB，杂波得到有效抑制。

4 结束语

在穿墙成像雷达中，由于墙体强杂波的存在，目标信号相对微弱，为了更好地进行成像就必须进行杂波抑制。为此本文在基于熵值法基础上提出一种基于拉普拉斯平滑处理的杂波抑制算法，解决了熵值法中因个别目标采样点数据的滤除导致信杂比降低问题。即在计算概率时采取拉普拉斯平滑处理，获得更准确的信源熵值，同时为了提高信杂比改善增量，进行一次迭代处理。由成像结果可以看出，本文所提算法杂波抑制效果以及信杂比改善量明显优于熵值法。理论推导以及程序仿真实验验证充分说明了本文方法对于穿墙成像雷达理论研究与实际工程具有一定的参考和指导意义。