三维移动目标无源定位算法

王小英1江怡帆2赵 悦34

(1.华北电力大学数理学院， 北京 102206; 2.多伦多大学统计系， 加拿大M5S 2E8; 3.北京应用物理与计算数学研究所， 北京 100094; 4.东北师范大学数学与统计学院， 吉林长春 130024)

0 引言

辐射源无源定位技术[1-3]是电子战的一个重要组成部分，无论是传统的战略战术电子侦察，还是电子干扰，都离不开利用目标辐射源的信号或外辐射源的信号对目标进行定位。无源定位技术能在自身不辐射的条件下，隐蔽地确定辐射源的位置，具有作用距离远、抗干扰能力强的特点，对于提高系统在复杂电子战环境下的生存能力和作战效能具有十分重要的作用，因此无源定位技术的研究越来越受到各国的重视。

无源定位的目标是得到辐射源的高精度二维或三维空间位置，现阶段的多站无源定位技术主要有: 到达方位(AOA)定位[4-5]、到达时差(TDOA)定位[6]、多普勒频差(FDOA)定位[7]以及其中两种或三种联合定位的技术[8-9]等。文献[10]利用辐射源脉冲到达时间(TOA)、到达方向(DOA)，以及方位角变化率信息，基于运动学原理，实现了固定单站对三维运动辐射源的无源定位算法。文献[11]提出了基于修正增益扩展卡尔曼滤波(MGEKF)，对三维运动辐射源的无源定位跟踪算法。

上述文献主要针对二维或三维空间固定辐射源无源定位技术进行了研究，对于机载、舰载移动目标的应用环境而言，三维空间的无源定位技术的研究还处于发展阶段。为解决精度和系统复杂度上的问题，本文深入分析了三维空间移动目标无源定位，基于目标辐射源脉冲到达时间(TOA)、到达方向(DOA)以及方位角变化率，提出了代数几何概率的无源定位方法，并给出了每一时刻目标位置误差随时间变化的关系，最后通过数值模拟展示了定位方法的精度。以期在实际应用中对近空间或邻近空间中高速移动目标进行三维快速定位，更好地提供无源侦察中移动目标的方位情报信息。

1 三维移动目标代数几何概率定位算法

由于单个侦察机在接受电磁信号时无法计量信号来自多远，它只能给出在什么时间收到，什么方位进入的信号。这样，除了一些特殊情况外，无源定位需要多观测站(或多点)提供信息，协同定位。这种协同表现为定位站需要在空间移动、多次测量，或者多站间要有信息通信(地面侦察站尽量隐蔽、突发)。

为了算法推导的便捷，不失一般性，本文假设3个侦察站处于同一海拔高度，不难发现本文算法可以推广到一般情形。在此假设下侦察站的到达角只需用信号到达方向与水平面(基准面)的夹角来表示即可，如图1所示。

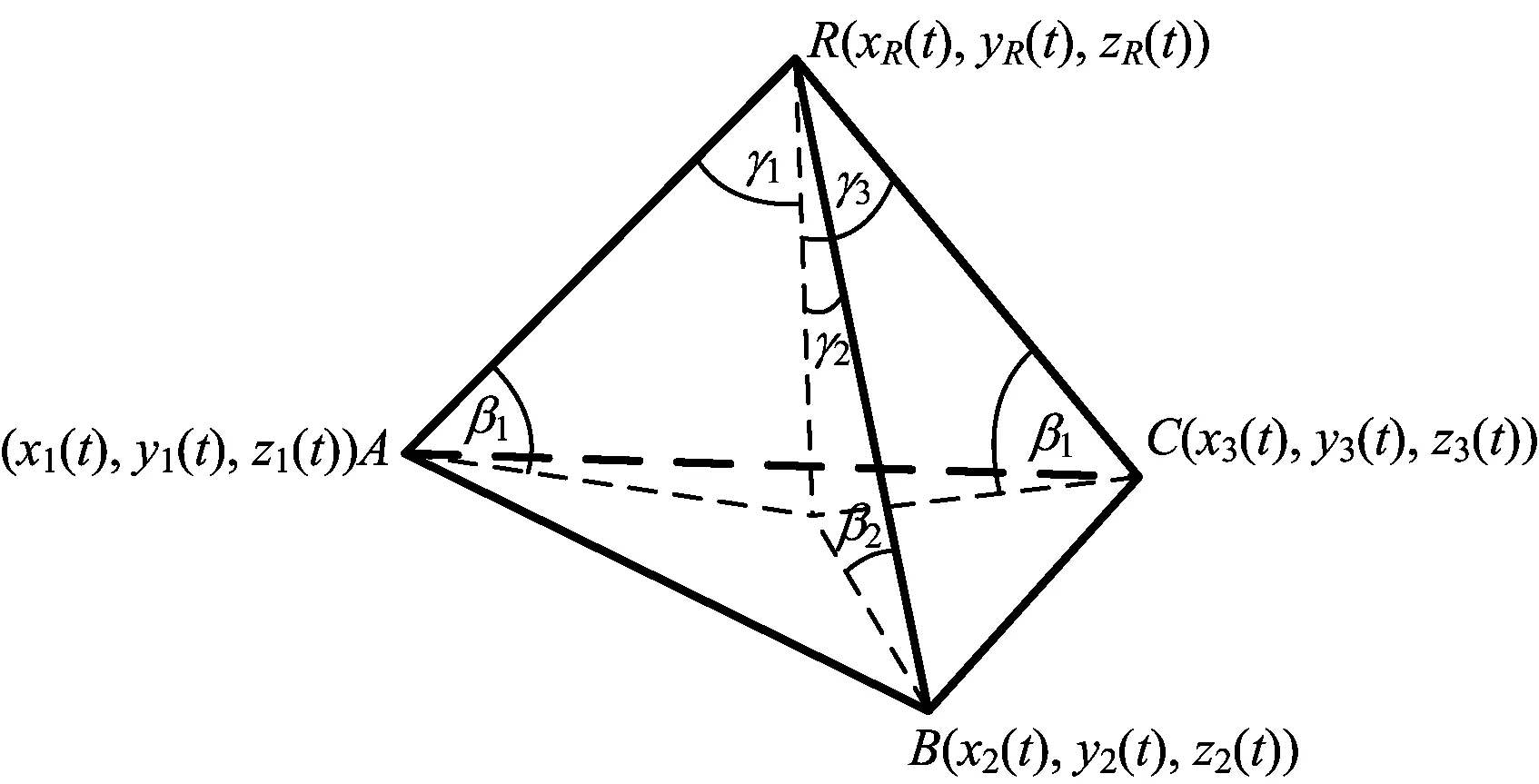
图1 三观测站到达角的几何关系

Cov(xi(t),yi(t),zi(t))=

(1)

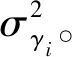
Cov(γ1(t),γ2(t),γ3(t))=

(2)

3个侦察站到达角的表达式为

(3)

(4)

(5)

通过计算可以推出目标位置(xR,yR,zR)的表达式。令

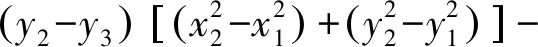
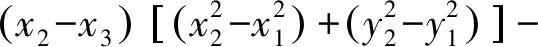
C=(x2-x1)(y2-y3)-(x2-x3)(y2-y1)

D=(y2-y3)(tan2γ1-tan2γ2)-

(y2-y1)(tan2γ3-tan2γ2)

E=(x2-x3)(tan2γ1-tan2γ2)-

(x2-x1)(tan2γ3-tan2γ2)

计算可得

(6)

(7)

(D2+E2)(zR-z1)4+[(A-2x1C)2+

(8)

在给出由侦察站的位置以及目标电磁波辐射到达角误差引起的辐射源位置协方差矩阵之前，首先给出下面一个关于复合函数求协方差矩阵的链式法则。

Cov(f1，f2，f3)=

(9)

式中

Cov(f1,f2,f3)=

证根据全微分定义可得下面的近似等式(m,n=1,2,3):

(10)

另一方面，经计算可得

(11)

式中(m,n=1,2,3)，

比较式(10)和式(11)可以得到复合函数协方差矩阵的链式法则式(9)。

由上面的引理，可以得到辐射源位置的协方差矩阵为

Cov(xR(t),yR(t),zR(t))=

(12)

式中，

2 算法及数值模拟

本节将对提出的三维空间移动目标无源定位算法进行数值验证。相关参数设置如表1所示，分别针对随机变量不同方差以及到达角不随时间变化的数值模拟结果如图2～4所示，目标位置以及椭球半径随方差变化的模拟数据如表2所示。

表1 数值模拟AOA方法参数设置

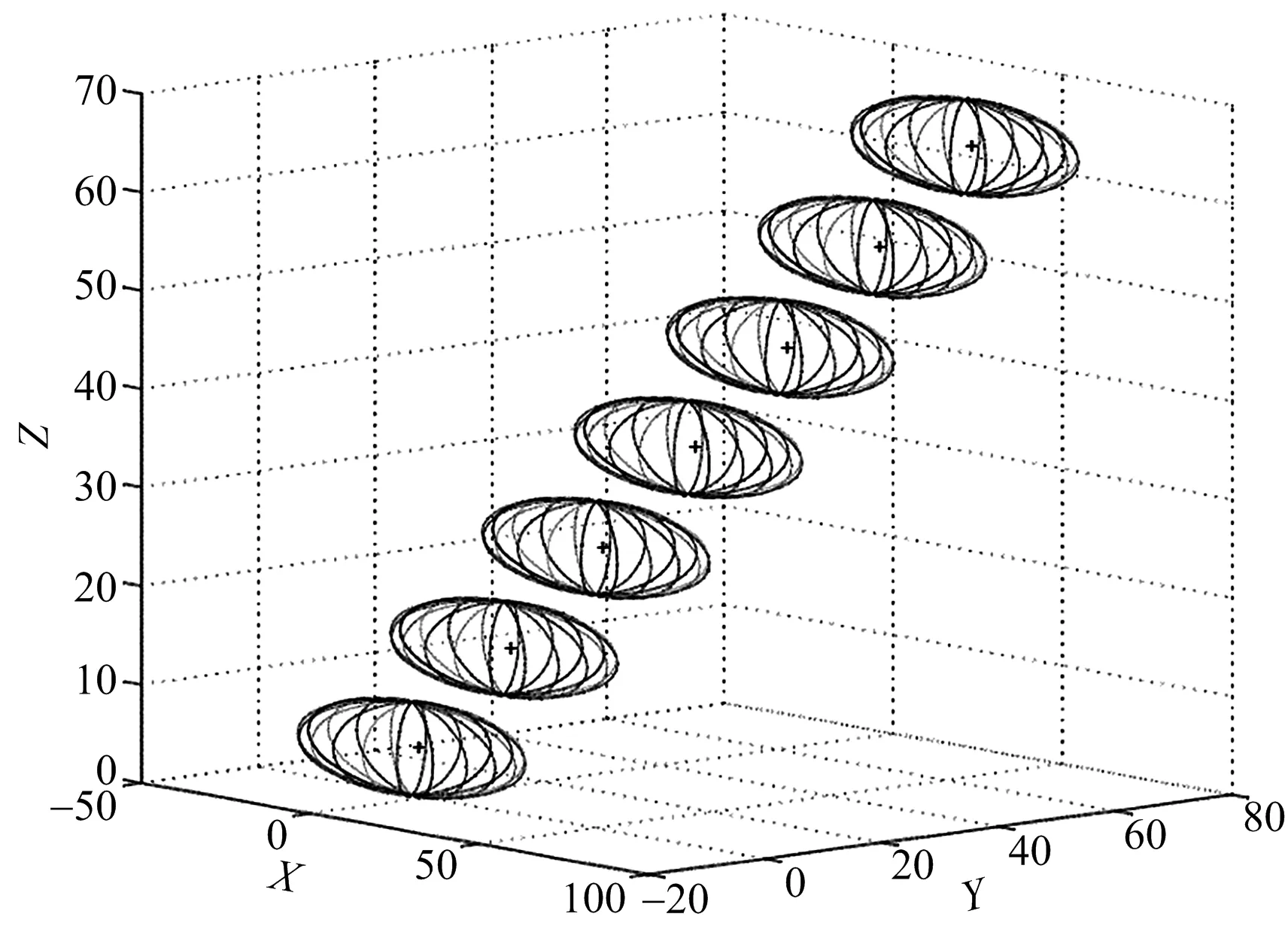
图2 三侦察站到达角不随时间变化情形(γ1=π/4,γ2=π/6,γ3=π/3;随机变量方差均为1)

图3 三侦察站到达角不随时间变化情形(γ1=π/4,γ2=π/6,γ3=π/3;随机变量方差均为0.1)

图4 三侦察站到达角不随时间变化情形(γ1=π/4,γ2=π/6,γ3=π/3;随机变量方差均为0.01)

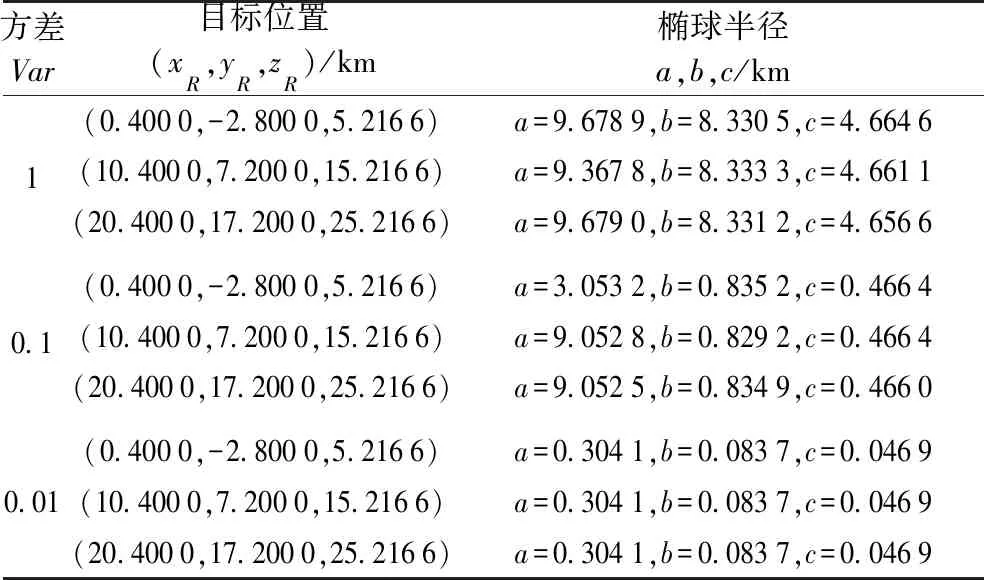
方差Var目标位置(xR,yR,zR)/km椭球半径a,b,c/km1(0.4000,-2.8000,5.2166)a=9.6789,b=8.3305,c=4.6646(10.4000,7.2000,15.2166)a=9.3678,b=8.3333,c=4.6611(20.4000,17.2000,25.2166)a=9.6790,b=8.3312,c=4.65660.1(0.4000,-2.8000,5.2166)a=3.0532,b=0.8352,c=0.4664(10.4000,7.2000,15.2166)a=9.0528,b=0.8292,c=0.4664(20.4000,17.2000,25.2166)a=9.0525,b=0.8349,c=0.46600.01(0.4000,-2.8000,5.2166)a=0.3041,b=0.0837,c=0.0469(10.4000,7.2000,15.2166)a=0.3041,b=0.0837,c=0.0469(20.4000,17.2000,25.2166)a=0.3041,b=0.0837,c=0.0469

从表2和图2～4中可以发现，随着随机变量方差的减小，目标位置估计区域椭球的半径也在减小，即定位精度越来越高，这为实际中三维移动目标快速并精确定位提供了依据。

另外对于到达角随时间变化的数值模拟结果如图5～7所示，目标位置以及椭球半径随方差变化的模拟数据如表3所示。

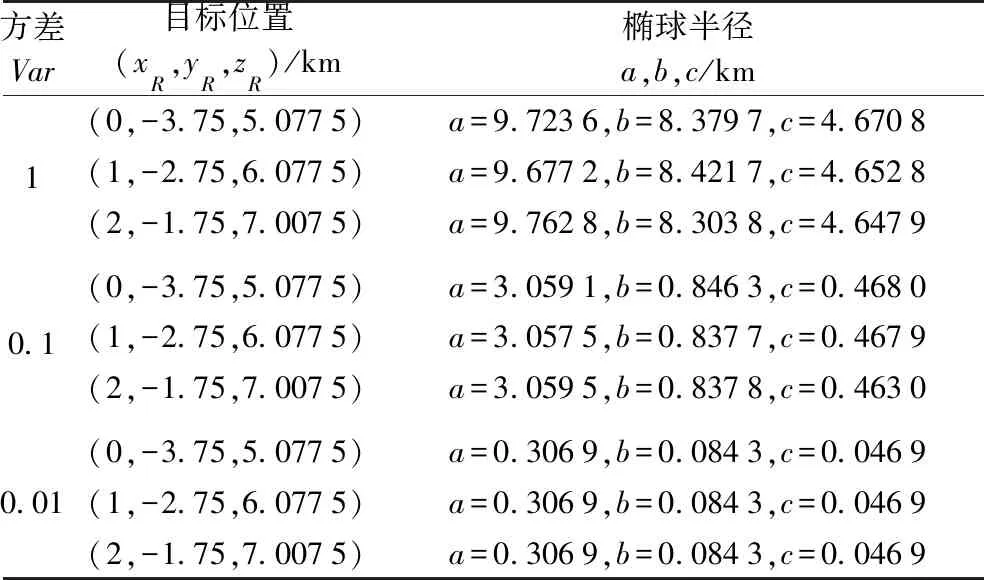
表3 目标位置和椭球半径随方差变化结果(AOA随时间变化)

图5 三侦察站到达角随时间变化情形(随机变量方差均为1)

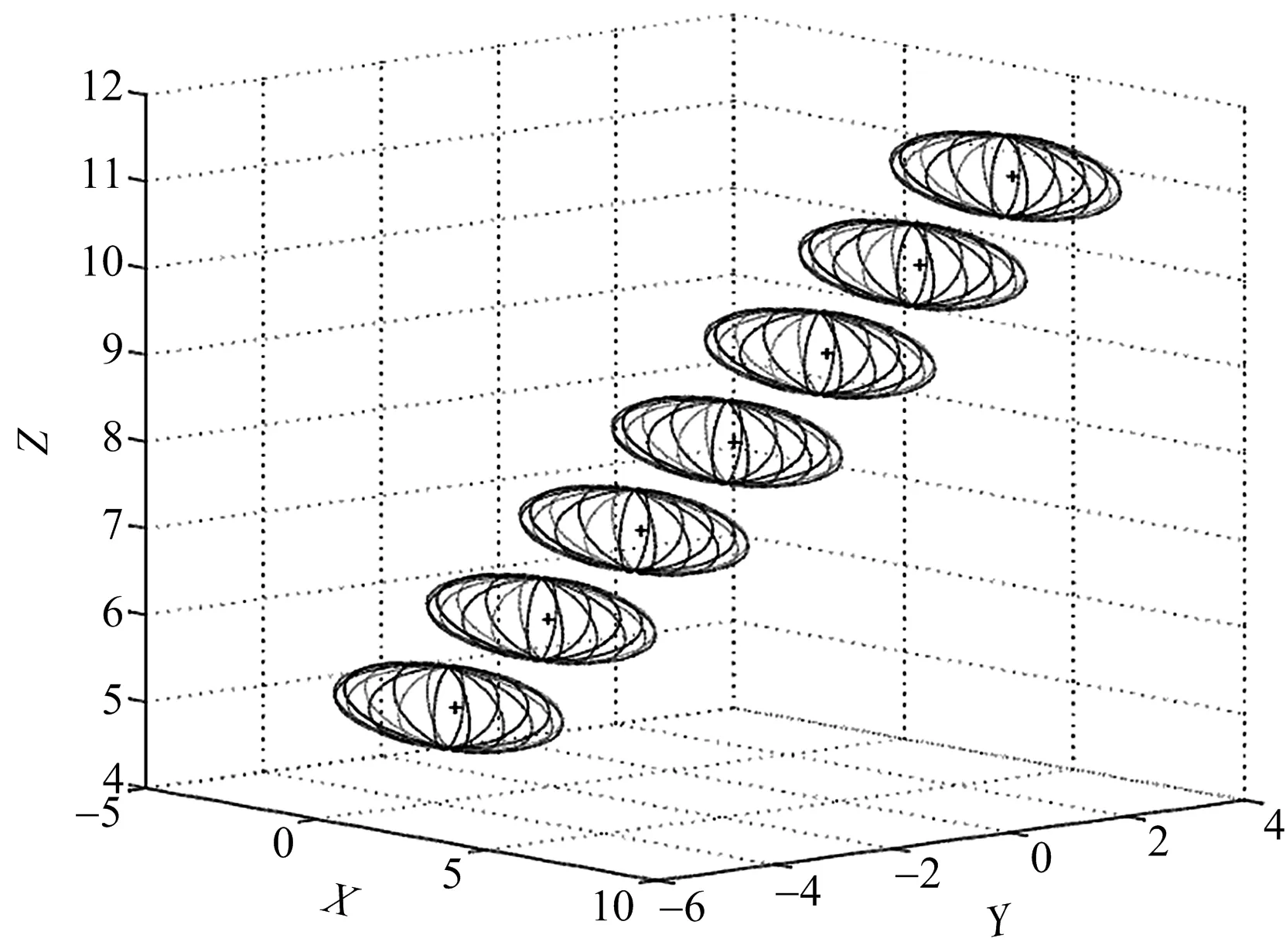
图6 三侦察站到达角随时间变化情形(随机变量方差均为0.1)

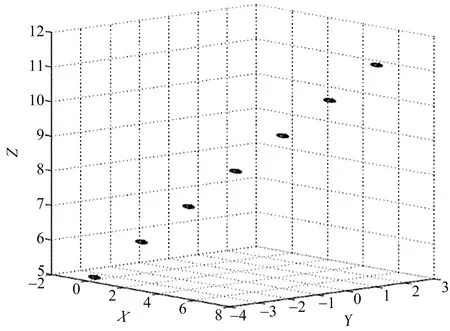
图7 三侦察站到达角随时间变化情形(随机变量方差均为0.01)

3 结束语

本文提出了基于到达方位信息的常态侦察时三维移动目标无源定位代数几何概率方法，并通过数值模拟展示了所研究定位方法的精度。本文所提的方法可为近空间或邻近空间中高速移动目标的三维快速定位提供一定的借鉴意义。为进一步提高定位精度，下一步可考虑基于到达时间差的方法和基于到达时间差/到达频率差的方法对三维移动目标进行定位。