顺向连接 逆向对称——二次函数中线段“和”最小问题

罗文武

(重庆市荣昌区宝城初级中学 402460)

近年来，二次函数中“线段和最小”的综合题常见于各地中考压轴题，这一考点要运用对称变换来进行处理，但什么时候作对称点，作哪个点的对称点，以哪条直线为对称轴作对称，这让我们的老师和同学们很困惑.本文针对几种问题情景谈谈自己的观点，与大家共勉．

一、缘起

问题情景1：已知直线l及两点A，B，在直线l上作一点P，使PA+PB最小．

如图1，点A，B在直线l两侧，我们在直线l上任找一点P，连接PA，PB，这时，PA+PB可以看成路径“A到P到B”，这个路径穿过了直线l，我们称这种情形为顺向．显然，要使PA+PB最小，必须使点A，P，B在同一直线上，故连接AB交直线l于点P，如图2，则点P使PA+PB最小，这样，我们可得出：顺向连接；如图3，点A，B在直线l同侧，我们在直线l上任找P，连接PA，PB，这时，PA+PB可以看成路径“A到P到B”，这个路径通过动点P所在直线l反射到定点A所在的同侧区域内，我们称这种情形为逆向．显然，要确定点P的位置，我们应该作点B(或点A)的对称点B1，将逆向的“A到P到B”转化为顺向的“A到P到B1”模型，再连接AB1交直线l于点P，连接PB，如图4，则此时的点P使PA+PB最小，最小值为线段AB1的长度，这样，我们可得出：逆向对称．从这简单的情形就得到“顺向连接，逆向对称”．

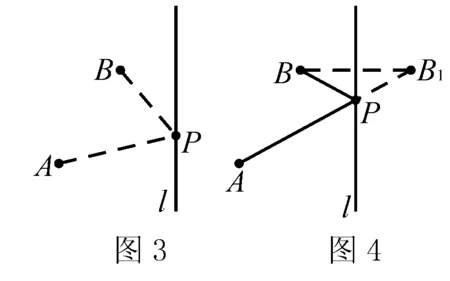
思维小结：顺向连接，应用“两点之间，线段最短”的原理，而逆向对称则是将逆向利用对称转化为“顺向”，同时，要清楚的是作定点A或B的对称点，是以PA+PB中的动点P所在的直线为对称轴的．

二、提升

问题情景2： 已知直线l1，l2及两定点A，B，在直线l1上作一点M，在l2上作点N．

我们首先看点A，B在两直线外侧的情形，如图5，使AN+MN+MB最小．显然，路径“A到N到M”及路径“N到M到B”都是逆向，故将定点A，B分别作关于直线l2，l1的对称点A1，B1，连接A1B1交l1于M，交l2于N，连接AN，BM，将逆向的“A到N到M到B”转化为顺向的“A1到N到M到B1”，则此时AN+MN+MB最小，最小值为A1B1的长度，如图6(也可将定点A作关于直线l2的对称点A1，再作A1关于直线l1的对称点A2，连接A2B交l1于点M，连A1M交l2于N，变逆向“A到N到M到B”为顺向“A2到M到B”).如果点A，B在两直线同侧，如图7，要使AM+MN+NB最小，根据“顺向连接，逆向对称”，我们应该作定点B关于与它所连的动点N所在直线l2的对称点B1，连接AB1交l1于点M，交l2于点N，连接BN，变逆向“B到N到M到A”为顺向“B1到N到M到A”此时点M，N使AM+MN+NB最小，最小值为AB1的长度，如图8．

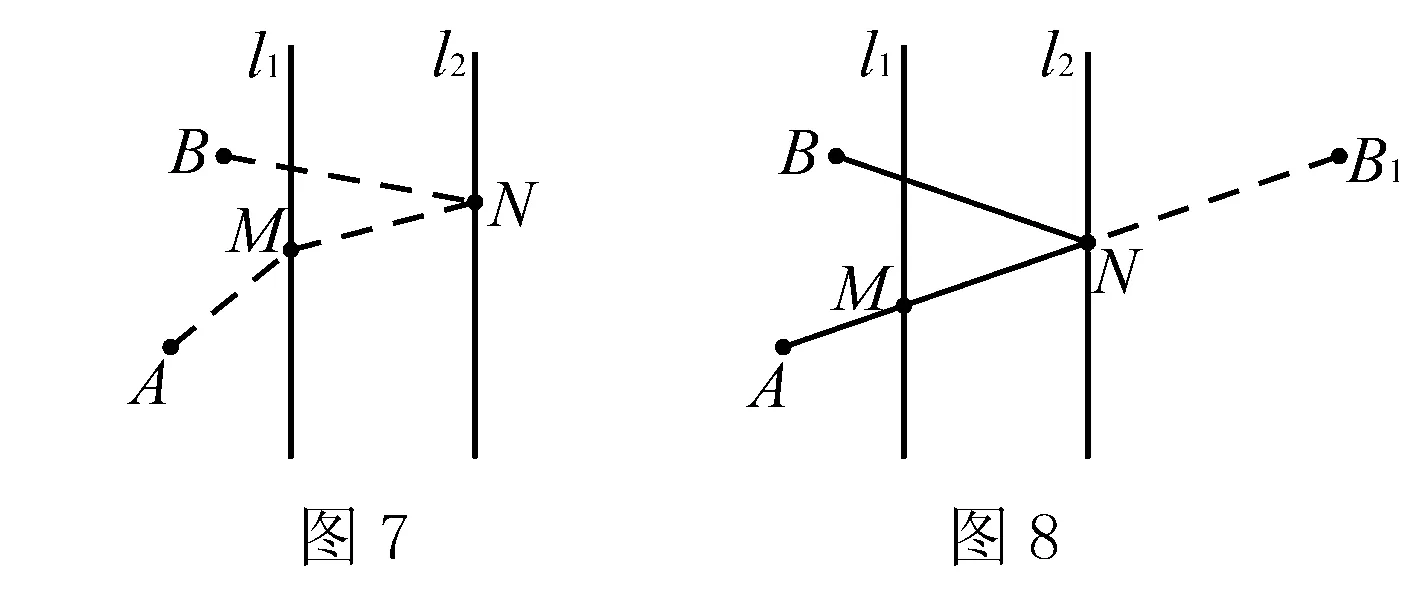
思维小结：对于“逆向”，我们作定点关于与之相连的动点所在的直线的对称点，变“逆向”为“顺向”，比如图8，“A到M到N”是顺向，不作对称，而“M到N到B”是逆向，应该作“定点B”的对称点B1，对称轴就应该是与这个定点B相连的动点N所在的直线l2，这样就都转化为“A到M到N到B1”的“顺向”，然后连接即可题解，也就水到渠成了．

三、应用

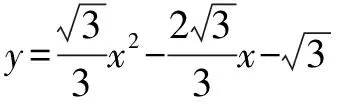
(1)求直线AE的解析式；

(2)点P为直线CE下方抛物线上的一点，如图10，连接PC，PE,当△PCE的面积最大时，连接CD，CB，点K是线段CB的中点，点M是CP上的一点，点N是CD上的一点，求KM+MN+NK的最小值．

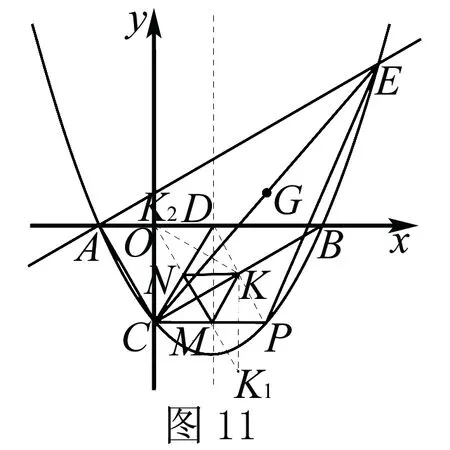
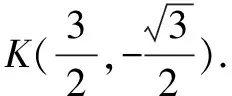
思维小结：“K到M到N”及“M到N到K”都是逆向，作“定点K”的对称点，对称轴分别是M，N所在的直线CP，CD．

四、拓展

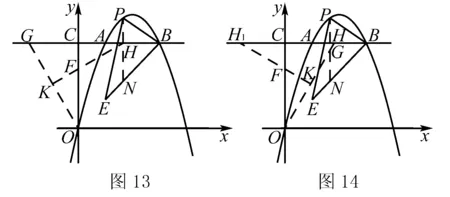
例2(2018年重庆中考A卷改编)如图12，在平面直角坐标系中，点A在抛物线y=-x2+4x上，且横坐标为1，点B与点A关于抛物线的对称轴对称，直线AB与y轴交于点C，点D为抛物线的顶点，点E的坐标为(1，1)．

五、升华

投出一粒石，激起千层浪．“顺向连接，逆向对称”是我在二次函数线段和最小值中的一个新发现，也是一大突破点.子曰：“疑是思之始，学之端．”它的每一个环节，对我来说都是新的尝试和挑战！要想在数学压轴题中乘风破浪，披荆斩棘，我们必须要有独到的创新思维和创新方法，让创新变得有理可依，更加高效！