谈如何提高初中数学课堂的实效性
林天国
摘要:在初中数学课堂上,教师要有效地激活学生的数学学习兴趣,增强学生动手、动脑的能力,并积极创设有效的教学情景,提高课堂的实效性。
关键词:创设情境;动手动脑;高效课堂
中图分类号:G633.6 文献标识码:A 文章编号:1992-7711(2019)03-0109
在初中数学课堂上,教师要让学生积极地融入课堂活动,这就要求教师更要关注数学课堂教学的实效性。这就应该对学生动手、动脑的能力加强培养,也应该对教学情境的有效创设提出更高的要求。
情境是“一个人在进行某种行动时,所处的社会环境”,它是认知活动的信息来源,数学情境是含有相关数学知识和数学思维方法的情境,它能为数学问题的提出和解决提供相应的信息和依据。一般地,数学情境能够使人产生一种“身临其境”的真实感,符合语言表达的情境,具有可操作性,而以图像语言表达的情境则具有直观性。如何实施这一过程?具体的做法是通过直观显示情境,质疑形成探究情境,模拟实践体会情境等,使学生在学习实践中形成一定的内心体验,以增强学生积极参与的意识,从而高效地完成教学任务。
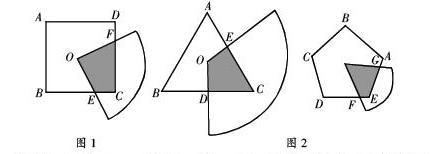
通过实验,展示实物,制造悬念,讲数学典故等方法,调动学生的非智力因素,特别是内在动机,给他们以强烈的求知欲和饱满的热情学习新知识。例如:1.操作与证明:如图1,O是边长为a的正方形ABCD的中心,将一块半径足够大,圆心角为直角的扇形纸板的圆心放在O处,并将纸板绕O旋转,求证:正方形ABCD的邊被纸板覆盖部分的总长度为定值a。
2. 尝试与思考:如图2,将一块半径足够长的扇形纸板的圆心放在边长为a的正三角形或边长为a的正五边形的中心O处,并将纸板绕O点旋转,当扇形纸板的圆心角为____度时,正三角形的边被纸板覆盖的部分为定值a,当扇形纸板的圆心角为______度时,正五边形被纸板覆盖的部分的总长度也为定值a。
3. 探究与引申:一般地,将一块半径足够长的扇形的圆心放在边长为a的正n边形的中心O处,并将纸板绕O点旋转。当扇形纸板的圆心角为360°/n时,正n边形的边被纸板覆盖的部分的总长度为定值a,这是正n边形被纸板覆盖部分的面积是否也是定值?若为定值,写出它与正n边形面积之间的关系,若不是定值,请说明理由。让学生在亲手操作中学习知识,并把正方形推广到正三角形和正五边形,进而引申到任意多边形中去,体现了从特殊到一般的研究数学问题的方法。对学生观察、猜想、探究能力方面作了很好的考查。
教师精心设计提出问题的过程,通过质疑,引导学生进行探究,激发学生思维,使学生随时处于积极思考的状态中获得成功的求知欲望。
情境(1)你能说明“糖水加糖变甜“这一事实吗?
情境(2)建筑学规定:民用建筑的采光度等于窗户面积与地面面积之比,但窗户面积必须小于地面面积,采光度越大,说明采光条件越好。问增加同样的窗户面积与地面面积后,采光条件是变好还是变坏。说明理由。
教师应该从学生的思维中适当挖掘出一些思维亮点,从而体现学生为主体的新课程理念,例如关于“(-3)×(-4)=9”的说法,这是一位学生得出的结论。虽然这位学生得出的结论是错误的,但我们应该让学生大胆地说出自己的想法,说一说(-3)(-4)=9是怎样来的,并对这位学生敢于独立思考的精神给予肯定和鼓励,与此同时,洞察该生的“思维根源”到“思维观念”这一环节。根据该生所述的“在数轴上,站在-3这个点上,因为是乘以-4,所以要沿着数轴向相反方向——右方移动4次,每次移动3格,结果是9”,思维根源是北大实验教科书七年级上册46页的“利用数轴表示加法运算过程”相关内容,因而发展为上面的“思维理念”。错误根源在于忽略了“以原点为起点”这句话。我们循着这位学生的思维展开:该生思考3×4,在数轴上站在3这点上,因为3×4所以要沿着数轴向上正方向(相同方向)移动4次。结果是15,而3×4=12.错在哪里?3×4=3+3+3+3 ,在数轴上,以原点为起点,应向数轴正方向移动3个单位连续移动4次,结果是12.即站在从0~3处本身就已移动一次。3(-4)就是站在原点上应向数轴正方向移动3格(单元格),因为是乘以-4,所以要在原点沿数轴向相反方向(相对于3的方向)移动4次,每次3格结果是-12. (-3)×(-4)就是站在原点上应向数轴反方向(左方)移动3格,又因为乘以-4,所以要站在原点上沿数轴向相反方向(相对于-3的方向)右方连续移动4次,每次3格,结果为12。
其次,新课程理念中还有一个重要环节,加强培养学生动手动脑的能力,初中教材中抽象的内容最能为学生提供动手动脑的机会,教师应充分利用这些内容,创设情境,引导学生动手动脑,提高课堂效率。如在讲解“勾股定理”这一内容前,可以让学生测量出课本的长和宽,用c2=a2+b2借助计算器算出c的值,然后让学生测量验证。当学生露出惊讶之色时,趁热打铁引入新课。如此一来,学生们感受了勾股定理的神奇,从而激发了学习兴趣,既培养了学生的动手能力,又完成了教学目标。
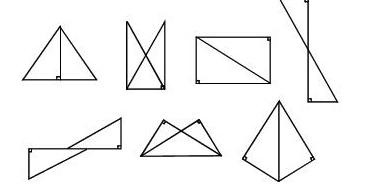
三角板是初中学生必备的学具,在讲解“两个直角三角形全等”可以让学生拼出各种各样的图形。
通过图形的不同组合,让学生的思维朝多方向发展。当然还可以用三角板拼出各种角度。这样既培养了学生的动手能力,又培养了学生的创造性能力。
总之,随着新课改和高效课堂理念的不断普及,课堂应更注重以学生为主体,教师为主导的教学理念,高效课堂对教师数学课上如何创设有效情境和如何增强学生动手动脑能力都提出了更高的要求。只有创设最有效的教学情境,并最大限度发挥学生动手动脑能力,这样的课堂才是最具有实效性的。
(作者单位:福建省莆田市青璜中学 351111)

