基于能量法与遗传算法的直齿轮振动分析与优化

韩 炜，田韶鹏

(1.武汉理工大学 现代汽车零部件技术湖北省重点实验室，湖北 武汉 430070；2.武汉理工大学 汽车零部件技术湖北省协同创新中心，湖北 武汉 430070)

在实际生产加工过程中，为了改善齿轮的传动性能，减小齿轮的振动和噪声，通常采用齿轮修形方法，即针对性地去掉轮齿的部分材料来消除轮齿的碰撞冲击，从而实现动力的平稳传递。

目前国内外对于齿轮修形已经做了大量的研究。Sun等[1]基于薄片理论建立了修形齿轮的时变啮合刚度模型，并依据该模型分析了齿轮不同参数对啮合刚度的影响。Ma等[2]利用有限元方法研究齿轮的修形量与齿轮的啮合刚度和传递误差之间的关系，并且分析了与齿轮振动特性的关系。陈洪月等[3]对渐开线直齿轮的传递误差进行研究，利用多目标遗传算法分析了修形量、修形起始点和修形曲线与齿轮传递误差的关系。杨丽等[4]提出一种基于Kriging模型和遗传算法的齿轮修形优化算法，并通过实例证明了该算法的修形有效性。笔者根据已有的研究，结合齿廓修形理论，首先基于能量法建立了齿轮啮合刚度计算模型并验证了该方法的有效性， 然后以齿轮的传递误差峰值为优化目标，利用遗传算法确定了齿轮的修形参数，最后利用实例验证了模型和计算方法的有效性。

1 齿轮修形原理及方法

1.1 齿向修形原理及方法

齿向修形是指为了弥补齿轮的受载变形情况，在齿向方向上去除一定的材料，使齿轮的受力主要在齿面中心的位置。通常使用的齿向修形方法是齿向修鼓，如图1所示。对齿轮进行修鼓可以有效地弥补齿轮由于加工安装误差和受到载荷影响时所产生的变形。

图1 齿向修鼓原理

齿向鼓形量Cc的选择是一个非常重要的问题，其大小对齿轮的受载性能有很大的影响。通常修形时参考经验公式，由ISO标准给出的鼓形量计算公式为[5]：

Cc=0.5Fβx

(1)

式中：Fβx为等效歪斜度。

1.2 齿廓修形原理及方法

齿轮在运动工作时会发生啮入啮出的碰撞冲击，利用齿廓修形可以有效避免这一现象，齿廓修形通过在齿轮的齿面方向上去除一定的材料来使主从动轮的基节大小相同，从而使齿轮啮合更加精确。齿廓修形原理如图2所示。齿廓修形方案的确定主要包括3个参数：最大修形量Δmax，修形长度L和修形曲线。最大修形量Δmax会对齿轮的振动和噪声产生很大的影响，通常要在实际的工作条件下进行试验来确定，这里根据ISO标准采用经验公式[6]计算。

(2)

式中：KA为工况系数；Ft为圆周力；b为齿宽；εα为端面重合度；Cγ为齿轮啮合刚度。

图2 齿廓修形原理

修形长度L在齿廓修形中也是很重要的参数，一般分成长修形和短修形，根据不同的情况采用不同的修形长度，如图2所示。长修形的修形长度是指从单齿啮合区的终点到齿顶的距离，短修形的修形长度为长修形的修形长度的一半。修形长度的公式为[7]：

长修形L=Pb(εα-1)

(3)

短修形L=Pb(εα-1)/2

(4)

式中：Pb为基圆节距。

在齿廓修形中采用不同的修形曲线会对齿轮的动态性能产生不同的影响，通常使用的修形曲线有直线、抛物线和双曲线等[8]。其中直线修形方程为：

(5)

抛物线修形方程为：

(6)

式中：x为啮合位置的相对坐标，其中沿啮合线的方向，坐标原点取单双齿啮合的交替点位置；Δ为x处的修形量。

2 能量法计算轮齿啮合刚度

2.1 能量法计算啮合刚度原理

在分析轮齿的啮合刚度时，利用有限元方法可以获得相对精确的结果，但是这种方法需要花费大量的时间，计算效率较低。在对齿轮进行修形优化时，利用解析法计算齿轮的啮合刚度可以提高计算效率，为齿轮的修形优化提供基础，下面主要研究基于能量法计算齿轮的啮合刚度。

齿轮的啮合刚度分为5个部分：弯曲刚度kb、剪切刚度ks、压缩刚度ka、赫兹接触刚度kh和基体刚度kf[9]。在直齿轮传动过程中，每一个轮齿都可以当作为一个变截面悬臂梁，齿轮在受力的情况下会出现变形。直齿轮轮齿变截面悬臂梁模型如图3所示。

图3 直齿轮轮齿变截面悬臂梁模型

齿轮在外部载荷力F的作用下，会在齿轮内储存能量，这些能量可以分为4部分，即弯曲势能Ub、剪切势能Us、压缩势能Ua和赫兹势能Uh。根据材料力学理论，各部分势能可表示为[10]：

(7)

(8)

(9)

(10)

式中：F为沿啮合线方向的作用力，将其分解为沿水平方向的力Fa和沿竖直方向的力Fb；B为齿宽；d为在齿高方向上啮合点到基圆的距离；h为啮合点到轮齿中心线的距离；Ix为与基圆距离为x处的截面惯性距；Ax为横截面面积；E、G和ν分别为弹性模量、剪切模量和泊松比。

经过处理可以得出各部分的刚度为：

(11)

(12)

(13)

(14)

式中：α1为啮合力F与沿齿轮中心线的垂直方向的夹角。

轮齿由于受力发生形变，沿啮合线方向上产生的等效刚度即为基体刚度，可以表示为：

(15)

式中：L*、M*、P*、Q*为系数;uf为力Fb到危险截面的距离；Sf为齿根危险截面的宽度[11]。

综上所述，一对齿轮的综合啮合刚度为：

k=

(16)

式中：下标1和2分别表示主动齿轮和从动齿轮。

2.2 对比分析

在齿轮的啮合刚度计算和传递误差的计算中，通常采用有限元方法，这种方法的计算精度较高，但是花费时间较长。为了验证利用能量法得到轮齿啮合刚度的正确性，选取一对齿轮进行啮合刚度的分析，并且与有限元方法的结果进行比较。所研究的一对齿轮的参数如表1所示。保持从动轮不动，对主动齿轮施加转矩。齿轮的有限元模型如图4所示。

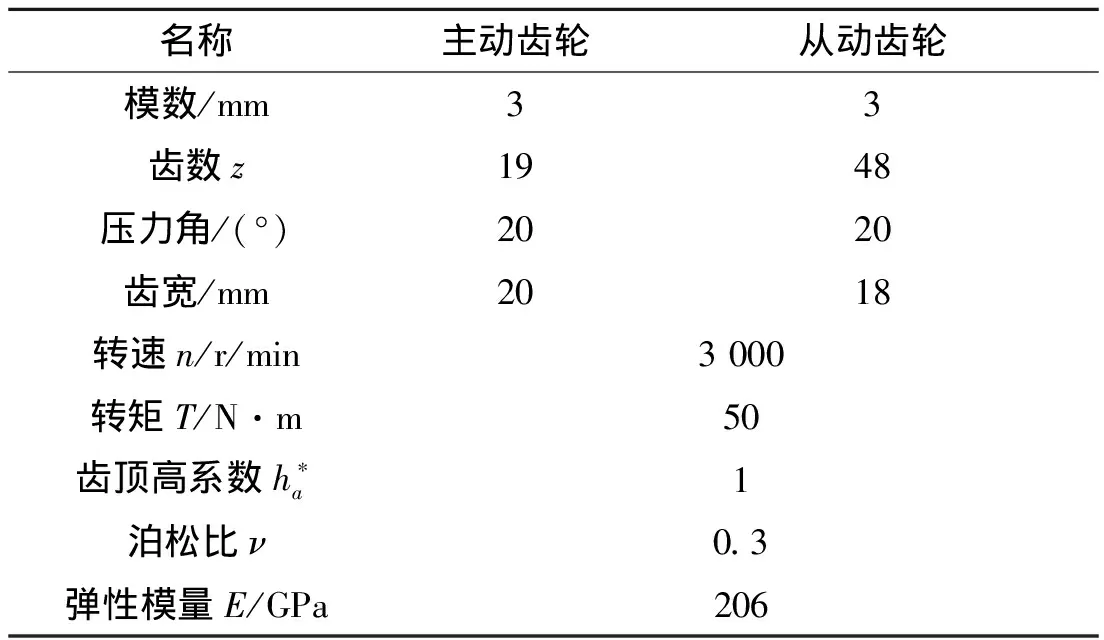
表1 齿轮参数

图4 齿轮有限元模型

将利用有限元方法得到的计算结果和基于能量法获得的计算结果两者比较，如图5所示，可以看出两种方案的结果曲线形状大致相同，分析得出的啮合刚度值十分接近。在单齿啮合区，利用有限元方法计算出来的最大啮合刚度为2.715×108N/m，能量法计算的最大啮合刚度为2.738×108N/m，能量法相对于有限元方法的计算误差为0.84%；在双齿啮合区，利用有限元方法计算出来的最大啮合刚度为4.671×108N/m，能量法计算的最大啮合刚度为4.724×108N/m，能量法相对于有限元方法的计算误差为1.12%。通过对比可以发现，能量法的计算结果与有限元法的结果基本相吻合，这验证了利用能量法计算的正确性，为下面的齿轮修形优化打下了基础。

图5 能量法和有限元法计算的啮合刚度对比

3 基于遗传算法的齿轮修形优化

3.1 遗传算法的原理

遗传算法是仿照自然界中的遗传进化原理的一种自适应全局优化算法[12]。

利用遗传算法产生问题的初始种群后，根据不同适应度情况来区分不同染色体的优劣情况，然后对种群进行遗传操作。其中，选择的过程可以产生性能更优的种群，变异和交叉可以生产新的个体，扩大搜索范围保证种群的多样性，这样获得的后代的整体适应度会越来越高。新的种群中遗传了上一代的优点，相比于上一代，性能更加优良。这样经过反复遗传进化之后，逐渐趋近于问题的最优解，直到满足终止条件。

3.2 遗传算法的优化过程

遗传算法主要分为问题的编码、初始种群的定义、适应度函数的分析以及选择、交叉、变异等操作。遗传算法的优化流程如图6所示。笔者以齿轮修形过程中的修形长度、最大修形量和齿向鼓形量为优化参数。首先对问题中的修形参数进行二进制编码，便于后续的计算。然后确定初始研究种群的规模和个体，初始种群规模个体数为n=100。然后定义适应度函数，分析群体中不同个体的适应度情况，设定适应度函数为齿轮传递误差的倒数，这样定义后个体的适应度值越大，说明所对应的质量越好，按此方法分析群体中每个个体的适应度值并根据大小进行排序。然后进行选择、交叉和变异操作。其中，选择操作采用轮盘赌的方式，即根据每个个体的适应度值在整个种群的适应度值总数里所占的百分比来确定每个个体能够被选择到进入下一代的几率。交叉和变异操作可以在种群中产生新的个体，这里设定交叉概率为0.5，变异概率为0.5。通过上述步骤能够获得新一代的个体，判断种群中个体的优劣情况。这样经过遗传进化到第K代时，若群体收敛则停止计算，否则继续进行迭代计算，直至满足终止条件。

图6 遗传算法优化流程

4 计算实例与分析

以一对直齿轮为例，验证所提出方法的有效性，齿轮的详细参数及工况参数如表1所示。利用所提出的遗传算法和能量法相结合的齿轮修形算法，对目标齿轮进行修形分析。根据齿轮啮合参数计算模型，应用Matlab软件进行编程，利用遗传算法搜寻齿轮修形参数的最优解，设定最大遗传进化次数为100，初始种群数为100，交叉和变异概率为0.5，最大修形量的搜索范围为[0 μm，8 μm]，修形长度的搜索范围为[0 mm，6 mm]，齿向鼓形量的搜索范围为[0 μm，8 μm]，完成齿轮修形参数的优化设计，遗传算法的优化搜寻过程如图7所示。

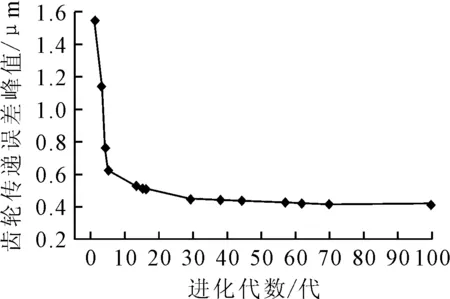
图7 遗传算法优化搜寻曲线

表2为基于能量法和遗传算法的齿轮修形方法、ISO修形方法以及修形前的齿轮修形参数及传递误差峰值的情况，图8为不同转矩工况下3种方案的齿轮传递误差峰值的比较。从表2可知，笔者提出的齿轮修形方法的传递误差峰值最小，且远远小于未修形的齿轮传递误差峰值。同时从图8可知，在不同的转矩工况条件下，笔者提出的齿轮修形方法总体优化结果较好，验证了基于能量法和遗传算法对齿轮进行修形优化的正确性和有效性。

表2 不同方法修形的优化结果

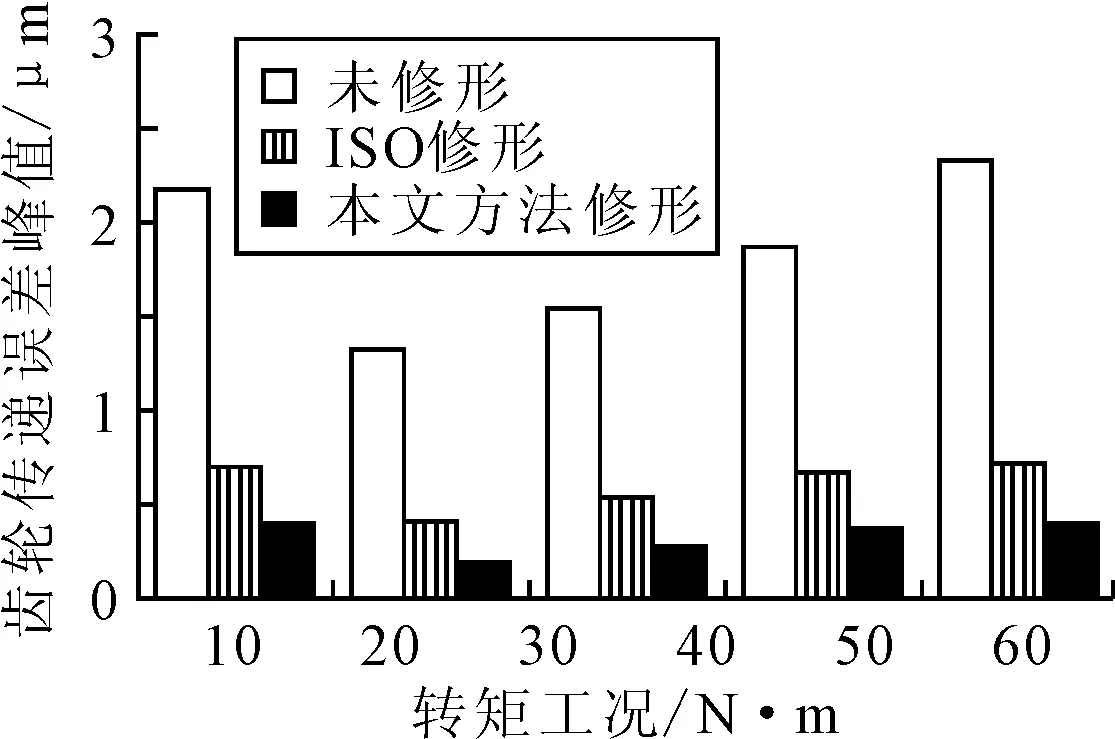
图8 不同转矩下齿轮传递误差比较

为了分析不同的齿轮修形方法对齿轮啮合应力的影响，分别对基于能量法和遗传算法修形的齿轮和未修形齿轮进行接触分析，修形前后的齿轮应力比较如图9所示。从图9可知，修形前的齿轮最大应力为1.219 MPa，基于能量法和遗传算法对齿轮进行修形后的最大应力为0.533 MPa，与未修形前齿轮的应力情况相比，该方法使齿轮的应力减小56.28%，可以在一定程度上减小齿轮上的应力。

图9 修形前后的齿轮应力图

5 结论

针对齿轮的振动噪声问题，根据齿轮修形理论，提出了一种齿轮修形方法，基于能量法和遗传算法得到如下结论：

(1)所提出的基于能量法的齿轮啮合刚度分析模型能够精确地计算轮齿在啮合时的综合啮合刚度，相比于有限元方法，利用能量法的计算效率更高，为齿轮修形优化设计打下了基础。

(2)利用能量法和遗传算法相结合，对齿轮的修形参数完成优化设计，相比于其他齿轮修形优化方法，利用能量法和遗传算法所得到的齿轮整体优化效果最好，能够有效地改善齿轮的振动噪声情况，为齿轮的性能优化问题提供了参考。