改进加权空间平滑MUSIC算法*
郑 棋 ,肖曼琳 ,施华杰 ,赵旻杰
(1.上海工程技术大学 城市轨道交通学院,上海 201600;2.上海地铁维护保障有限公司,上海 201600)
0 引 言
相干环境下信源波达方向估计是阵列信号处理领域里的一个重要分支,而基于空间谱估计的MUSIC算法,以其高精度的角度估计性能成为研究重点[1-2]。但在相干信源环境下,因信号子空间和噪声子空间不满足正交性,奇异的信源协方差矩阵的秩小于信号源数,使得该类方法失效。相干环境下信源波达方向估计的主要思路是先对阵列接收信号做预处理,在保持方位信息的前提下最大限度地对空间信源去相关,使信源协方差矩阵的秩恢复到信源数,并尽可能使其与对角阵,然后再利用常规的信号子空间类算法估计信源的到达角。
现有的对相干信源波达方向估计的算法,最典型的方法是空间平滑算法[3-4]。文献[5]对前向空间平滑算法(Forward Spatial Smoothing,FSS)进行了深入的研究和讨论;文献[6]提出了前后向空间平滑算法,通过增加子阵间的平滑次数,提高对相干信源的估计性能;文献[7]分析了前后向空间平滑算法的局限性,证明了前后向空间平滑算法的性能与相干信源的相对相位关系有较大的关系。为了进一步利用信号间的协方差矩阵信息,文献[8]提出了加权空间平滑算法(Weighted Spatial Smoothing,WSS),先利用常规的估计算法粗略得到信源方位信息,构造加权因子,实现相干信源的方向估计,但其角度估计精度受加权因子的优劣影响很大;文献[9]对构造加权因子提出改进,不需要预估计信源方向,直接利用阵列的输出数据计算最优加权矩阵,并得到信源方向;本文在文献[9]的基础上,提出了改进加权空间平滑算法(Main Weighted Spatial Smoothing,MWSS),利用子阵间的协方差矩阵的特殊关系,对加权矩阵进行空间平滑,充分利用子阵输出的自相关和互相关信息,从而进一步提高算法对相干信源的估计性能。
本文结构如下:第1节,对信号模型进行理论分析;第2节,介绍加权空间平滑算法。第3节,对原改进加权空间平滑算法进行分析;第4节,提出改进加权空间平滑算法;第5节,对上述算法进行仿真,验证其性能;第6节,总结改进加权空间平滑算法对相干信源的测向性能。
1 信号模型
假设天线的阵元数为M,阵元间隔为d的均匀线阵,有k个入射的窄带信号,入射角度分别为θk(k=1,2,…,K),以第一个阵元为参考阵,则信号入射到天线的示意图如图1所示。

图1 天线阵列模型
则第m个阵元的接收数据为:

式中,am(θk)为第m个阵元上第k个信号的响应矢量,sk(t)为第 k 个信源,nm(t)为第 m 个阵元的噪声值。
则线阵所接收的输入信号的向量形式:

定义阵列接收数据的协方差矩阵为:
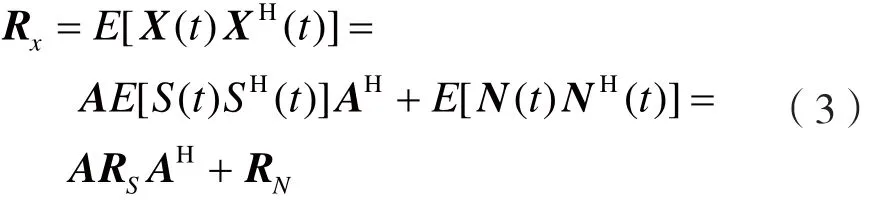
式中,RS和RN分别表示信号的协方差矩阵和噪声的协方差矩阵。
2 加权空间平滑算法
为解决相干信源的波达方向(Direc tion of Arriva,DOA)估计问题,文献[8]提出了加权前向空间平滑算法(Weighted Forward Spatial Smoothing,WFSS)。将前向阵列协方差矩阵中L2个p阶子矩阵进行加权平均,而权值的优化以平滑后等价的信源协方差矩阵与对角阵的逼进为约束条件。平滑后的协方差矩阵Rwf如式(6) 所示:

其中,Fi=[0p×( i-1)|Ip|0p×(N-i-p+1)],Fj=[0p×( j-1)|Ip|0p×(N-j-p+1)],wij为子矩阵Rij的加权系数,Rij为子阵i和子阵j的互相关协方差矩阵。定义加权矩阵W如式(5)所示:

其 中,W=(B·BH)+,(·)+表 示 复 共 轭 矩 阵,B=[b(θ^1),b(θ^2),…,b(θ^L)],b(θ^i)为预估计的信源导向矢量。可知加权矩阵W的选取与矩阵B有关,而矩阵B与信源方位有关。文献[8]采用不受相干信源影响的DOA估计算法进行DOA 的粗估,再选取矩阵B构造加权矩阵W。
3 原改进加权空间平滑MUSIC算法
文献[9]为了简单、有效地得到加权矩阵W,直接用阵列的协方差矩阵构造W,降低了WSS算法的信源方向预估计误差,提高了估计精度。原改进加权空间平滑MUSIC算法(Weighted Spatial Smoothing MUSIC,WFB-MUSIC)的实质是采用两次不同的方法划分原阵列,保证第1次划分的子阵数等于第2次划分的子阵的阵元数,即第1次划分的子阵的阵元数与第2次划分的子阵数相等。以此保证加权矩阵元素的数目等于被加权矩阵的个数,使加权因子与被加权矩阵相对应;具体步骤如下。
(1)分割天线阵列,分割后子阵的阵元数目为p,则子阵数为L=M-p+1,取L,p>m。采用前后向空间平滑算法得协方差矩阵为:

式中:J为置换矩阵,(·)*表示共轭。利用R1求加权矩阵W,即W=(R1)*,可知W为p×p维对角矩阵。
(2)分割天线阵列,保证所取子阵的阵元数L,子阵数为p,满足M-L+1=p。利用所求的W对前后向阵列协方差矩阵中p2个自、互相关矩阵Rij加权,得到新的协方差矩阵。

(3)对Rwf进行特征分解,应用MUSIC超分辨算法进行DOA估计。
4 改进加权空间平滑MUSIC算法
为了充分利用阵列输出的自相关和互相关信息,提高信号子空间与噪声子空间的正交性,本文在文献[9]的基础上提出了改进加权空间平 滑MUSIC算法(Main Weighted Spatial Smoothing MUSIC,MWFBMUSIC)。利用文献[9]原改进加权空间平滑MUSIC算法得到信源的预估计值 [θ^1,θ^2,…,θ^K],再利用预估值构建加权矩阵W,并对W进行平 滑处理,获得最优加权矩阵Wopt。具体步骤如下:
(1)利用文献[9]所得到的信源信息构造加权矩阵W:

(2)对加权矩阵W做平滑处 理,如图2所示,保证所取子矩阵为p×p维,平滑次数为M-p+1=M-(M-L+1)+1=L,求得加权矩阵 Wopt:


图2 加权矩阵平滑示意图
式中,Fk=[0p×(k-1)|Im|0p×(N-k-p+1)],可知 Wopt为 p×p维对角矩阵。
(3)利用所求的Wopt,对前后向阵列协方差矩阵中p2个自、互相关矩阵Rij加权,得到新的协方差矩阵Rmwf:

(4)对Rmwf进行特征分解,应用MUSIC超分辨算法进行DOA估计。
改进加权空间平滑MUSIC算法,相比加权空间平滑算法,不需要预估计信源方向,直接利用阵列的输出数据计算最优加权矩阵,提高了算法的稳健性。相比于原改进加权空间平滑算法,更加充 分的利用了阵列输出的自相关和互相关信息,提高了信号子空间与噪声子空间的正交性,对相干信源具有更好的角度估计性能。
5 算法仿真及性能比较
图3给出了上述MWFB-MUSIC算法、WFBMUSIC算法和MMUSIC算法在信噪比为10 dB时的DOA估计的性能仿真图。由图3可知,在多相干信源条件下,常规的MMUSIC算法已经 完全失效,不能 对相干信源的方向进行准确的估计,MWFB-MUSI C算法和WFB-MUSIC算法均能对信源方向有较准确的估计,但在10°,15°,25°方向角时,MWFB-MUSIC算法均比WFB-MUSIC算法具有更高的精确度,说明MWFB-MUSIC算法对相干信源具有更好的效果。实验2,采用阵元间距为半波长总阵元数M=16的均匀线阵。第1次空间平滑子阵的阵元数p1=5,第2次空间平滑子阵的阵元数p2=12。并假设相干信号源入射 角度为10°, 15°,30°,对MWFB-MUSIC算法和WFB-MUSIC算法在不同信噪比和快拍数下分别进行了10000次Monte Carlo实验。

图3 精确度仿真图
图4 和图5给出了上述MWFB-MUSIC算法和WFB-MUSIC算法在不同信噪比和快拍数下的均方根误差。由图可知,两种改进的加权空间平滑MUSIC算法均能对相干信源方向有较准确的估计,但同样的环境下MWFB- MUSIC算法明显比WFB-MUSIC算法的角度误差小,表明了MWFB-MUSIC算法在相同环境下优于WFB-MU SIC算法。

图4 不同信噪比估计方差比较

图5 不同快拍数估计方差比较
6 结 语
本文提出了一种改进加权空间平滑MUSIC算法(MWFB-MUSIC),该算法充分利用了阵列输出的自相关和互相关信息,提高了信号子空间与噪声子空间的正交性,使其对相干信源的 处理具有较好的效果。通过实验得 出,MWFB-MUSIC算法比原加权空间平滑算法(WFB-MUSIC)具有更高的精确度,在相同信噪比和快拍数下,MWFB-MUSIC算法均优于WFB-MUSIC算法,表明了新算法的有效性。

