基于机器学习梯度下降法的OAM对准算法*
张亚中,李玉箫,刘雨享,何 伟
(南京邮电大学,江苏 南京 210003)
0 引 言
近年来,互联网业务的迅速发展使信道容量接近饱和,频谱利用率也逼近香农限。而带有轨道角动量(Orbital Angular Momentum,OAM)的涡旋电磁波OAM涡旋电磁波具有相互正交的不同模态,有望通过开辟一个新的维度“模分复用”,提高频谱效率,实现同一频带承载更大的传输容量,因此成为通信领域和电磁波领域的热点。
当发射和接收阵列天线个数相同并且彼此完全对齐时,OAM系统的信道容量与多输入多输出(Multiple Input Multiple Output,MIMO)阵列信号相比拟。但是当发射接收机之间出现轴心偏角时,接收器可能会收到错误的模态,即产生模态串扰,导致误码率增大,系统性能下降,劣于MIMO系统[1-2]。
这是由于涡旋电磁波的螺旋传输特性,OAM系统要求收发天线轴心对齐,而由于用户接入数量的巨大和模态复用的存在,以及多址用户的动态性,都会引起波达角的时变,带来大量的信息丢失和不必要的功率损耗,这都对大型天线阵列精准对齐和应对多址用户动态变化提出了更高的要求。周叶青等人对OAM系统在不对齐情况下的接收功率谱密度进行了仿真,提出一种基于二分法迭代的轨道角动量无线通信中轴向对准的新方法[3]。但是这种对准算法收敛速度较慢,初始状态不容易满足,并且过程繁琐,不适合于机器的高效操作。本文提出一种基于机器学习梯度下降法的自动对齐算法,通过步长的逐步优化,降低收敛时间,过程简单,是一种适合于机器的高效算法。
1 基于梯度下降的对准算法
为了使发射天线和接收天线的轴心对准,OAM系统需要调整的参数主要有两种[4],第一,方向偏移,对应的参数为偏角γ;第二,水平位置偏移,对应的参数为水平坐标(x,y)。检验发射天线和接收天线是否对齐的指标有多种,本文中使用的是接收天线接收到的信号能量谱方差,当发射接收天线轴心对齐时,天线接收到的能量谱方差应达到最小。
当实际中的OAM系统中伴随着横向偏移和角度偏移时,文献[5]研究了偏移情况下的拉盖尔高斯电磁波,给出了对于发生轴偏移的OAM系统的谐波能量计算。文献[4]给出了一种基于二分法迭代求解能量谱方差最小的最优解的方法,但是这种方法对每一个参数初始状态的要求比较高,需要找到分别在最优解两侧的两个点。但是实际上,我们考虑到机器实际上不知道自己当前位置,只能获取当前位置相关数据,而这些数据由于环境因素以及发射机状态是一直在变化的,因此我们考虑用机器学习中的梯度下降法,依靠在当前位置以及相邻较近位置处接收机测量到的能量谱方差求出近似梯度。
机器学习算法中,解决无约束问题常用的方法有梯度下降法和最小二乘法。在最小化损失函数时,可以通过梯度下降法来一步步的迭代求解,得到最小化的损失函数和模型参数值。在微积分中,各个参数的偏导组合成的向量就是梯度。梯度的几何意义就是函数变化最快的地方,沿着梯度向量的方向,更容易找到函数的最值。但是梯度下降法不一定找到全局最优解,有可能是一个和局部最优解。但是如果损失函数是凸函数,梯度下降法得到的解就一定是全局最优解[6]。
收发天线需要调整的参数有三个,可以采用对参数逐一优化的方案,使发射天线和接收天线逐步对准,最终精确对准。为了使算法更优化,可以同时调整多个参数即多维梯度下降法,但是需要注意这时每个参数需要有不同的学习率。我们使用三维梯度下降法,得到在偏移状态下间隔较小每一点的数据,然后按照如下步骤:
(1)随机给出一组当前机器的偏移状态(x0,y0,γ0);
(2)确定损失函数,能量谱方差V(x,y,γ)。
(3) 测 出 机 器 当 前 位 置 (x0,y0,γ0)和 和 的(x0+Δ1,y0+Δ2,γ0+Δ3)能量谱方差,其中 Δi是一个很小的量,根据这两点算出处的梯度;

(4)接下来需要分别为三个参数确定合适的学习因子 ηi(i=1,2,3),进而确定步长 αi(i=1,2,3),即,即每个参数在当前位置每次移动的距离。

(5)确定是否所有的变量,梯度下降的距离是否都小于ε,如果小于ε则算法终止,当前(x,y,γ)即为最终结果。否则进入步骤6。
(6)做最小值优化,则更新所有的变量,以x为例,其更新表达式如下,y,γ同理。更新完毕后继续转入步骤3。
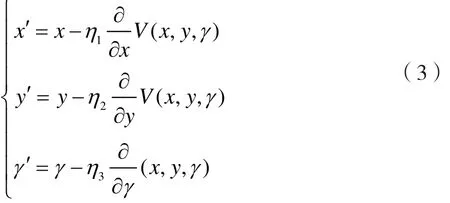
(7)算法调优。算法的步长选择。算法中步长α的取值取决于数据样本,其取值应从大到小,分别运行算法,使迭代效果中损失函数变小的取值有效,否则要增大步长。前面说了。步长太大,会导致迭代过快,甚至有可能错过最优解。步长太小,迭代速度太慢,很长时间算法都不能结束。所以算法的步长需要多次运行后才能得到一个较为优的值。
2 算法仿真
2.1 一维梯度下降法
对于每一个参数变量,能量谱都是关于变量的凸函数,因此使用梯度下降法最终都能得到损失函数的最优解。以参数x为例,任意选择一个初始状态,仿真时我们选择初始状态为x0=6,学习因子的选取与具体的数据样本有关,我们分别设置学习因子为0.7和0.3,循环终止状态为ε=0.1,按照上文中的算法步骤进行仿真。得到两种不同的收敛路径下,能量谱方差(用符号V表示)随横向偏移之间的曲线如图1所示。
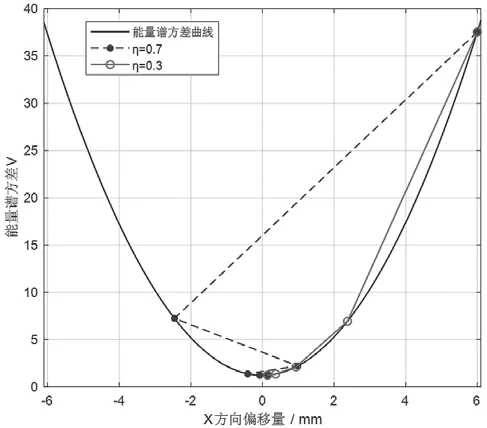
图1 一维梯度下降法收敛路径示意图
图1 中,曲线上的点表示实际可测量到的样本数据,实线表示η1=0.3时的搜索路径,搜索点只分布在最优解右侧;虚线表示η1=0.7时的搜索路径,搜索点分布在最优解两侧。由此可见,选择不同的学习因子时,收敛路径也会不同,但最终都将收敛到损失函数最小的最优解。我们列出了不同学习因子的搜索点,见表1。

表1 不同学习因子的收敛步数
由表1可见,不同的学习因子η会导致不同的收敛速率,选择合适的学习因子会使算法的效率有效提升。本次仿真中最优的学习因子为0.5。
2.2 多维梯度下降法
为例更加直观地看出算法的收敛路径,我们先仿真给出二个参数同时调整的示意图,实际中可以同时调整三个参数,各自步长的选取需要人为灵活调整。
按照梯度下降法求解能量谱方差随(x,y)的路径示意图如图2所示。其中实线路径表示学习因子较小的情况,虚线路径表示学习因子较大的情况,两者最终都收敛至凸函数的最优解。
多维梯度下降法可以提高算法效率,但是步长的确定需要根据实际的数据样本灵活调整。
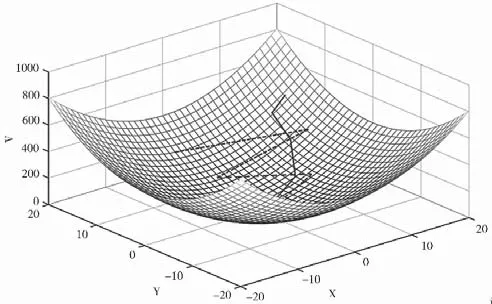
图2 多维梯度下降法收敛路径示意图
3 结 语
OAM涡旋电磁波在提高无线通信系统容量方面有很大的潜力,但是对收发天线的对准非常严格。本文我们建立了基于机器学习梯度下降法的OAM对准算法模型,仿真表明不同的学习率会导致不同的收敛速度,因此我们给出了一种优化学习率的方案,确定了此条件下的最佳学习率,实现了收发天线的快速对准。这种算法与前人的算法相比在实际中收敛速度更快,更适合于机器,对初始状态要求低。未来的工作将考虑多维梯度下降法,以及优化学习率的高效算法。

