面积法——解反比例函数面积问题的重要工具

左效平，张新华

（山东省沂源县徐家庄中心学校）

一、性质的认识

图1

二、性质的应用

1.根据面积求k值或表达式

（1）根据三角形面积求k值.

（1）求k和m的值；

图2

分析：第（1）小题根据反比例函数系数k的几何意义得到k值，然后把点A的坐标代入反比例函数解析式，即可求出m的值；第（2）小题先分别求当x=-3和x=-1时对应的y值，再根据反比例函数的性质确定y的取值范围.

解：（1）因为△AOB的面积为2，

所以根据性质可得k=4.

解得m=1.

当x=-1时，解得y=-4.

【评析】充分利用数形结合思想，将特征三角形面积与反比例函数中k值的意义准确地进行对接，并灵活进行计算是学习的一项重要要求.

教学中，首先要引领学生学会利用数形结合的思想去认识图象，并能够熟练地将三角形的面积与反比例函数中k值的意义有机结合起来，为成功解题奠定基础.其次，要求学生熟练运用反比例函数的性质，从k的属性、自变量的取值范围、函数值的取值范围三个角度去整体把握和应用性质.

（2）根据三角形面积之比求k值.

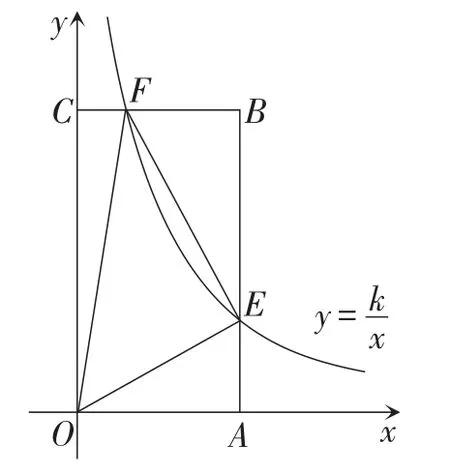
图3

解：因为四边形OABC是矩形，A(1，0)，C(0，2)，

所以可得点E的坐标为E(1，k).

根据题意，得点B的坐标为B(1，2).

所以矩形ABCO的面积为2.

所以四边形BFOE的面积为2-k.

因为S△OEF=2S△BEF，

故选A.

【评析】抓住点坐标的特点，巧妙构造相应矩形面积和三角形面积，并灵活运用这些面积表示已知图形面积是解题的关键.

教学中，教师要引领学生识别哪些图形的面积与反比例函数中的k值有关联，并指导学生活用分割法表示图形面积.

（3）根据四边形面积求k值.

图4

分析：S四边形OAPB=S四边形OMPN-k，因此点P的坐标成为解题的突破口.

解：因为点P(6，3)，

所以矩形OMPN的面积为18.

根据题意，得S四边形OAPB=S四边形OMPN-k.

所以k=18-12=6.

故答案为6.

【评析】正确进行图形面积的分割表示是解题的关键.

教学中，教师要有意识地引导学生正确处理好相关图形之间的面积关系，这是解决这类问题的主要工具之一，一定要让学生熟练掌握.

（4）根据三角形面积，三角函数值求k值.

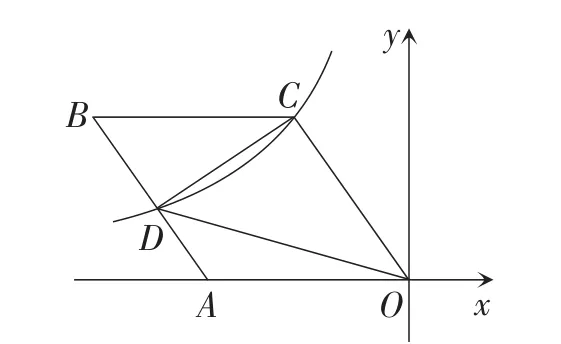
图5

图6

解：如图6，过点B作BE⊥Ox，垂足为点E，过点C作CF⊥Ox，垂足为点F.

因为S△COD=20，

所以菱形ABCO的面积为40.

设OF=3m，则CF=4m，OC=5m.

所以4m×5m=40.

所以m2=2.

所以|k|=24.

因为图象分布在第二、四象限，所以k=-24.

【评析】巧妙把S△COD转化为S△OCF是解题的关键.

教学时，要引导学生活用三个重要知识点：（1）△COD的面积是菱形ABCO的面积的一半；（2）活用三角函数值巧求三角形的面积；（3）求反比例函数图象点与坐标轴构成三角形的面积，这是确定k值的“金钥匙”.

2.根据反比例函数中的k值求面积

（1）根据两k值求面积.

图7

分析：四边形OCPD的面积是6，△OBD和△OAC的面积和是2，所以四边形PAOB的面积是4.

解：略.

【评析】此题为全国数学联赛初赛试题，竞赛题在一般的认识中都是非常难的，然而像上述这样具有一定技巧性的竞赛题越来越受到命题教师的青睐.这充分体现了素质教育的意义，也能反映学生的数学功底，更能折射出学生的数学智慧，只有拥有了数学智慧，才会灵活解题.

如何引导学生把数学知识升华为数学智慧是教师在教学中需要认真思考和强化落实的首要任务，只有把数学知识点升华为一个个数学智慧点，学生分析问题、解决问题的能力才能不断得以培养，学生眼高手低的问题才能得到有效解决.

（2）根据一次函数与反比例函数解析式求面积.

（1）求一次函数和反比例函数的表达式；

（2）求△AOB的面积.

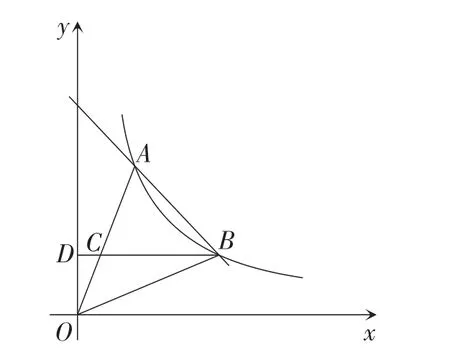
图8

所以a=2×3=6.

因为BD⊥Oy，交OA于点C，

所以yC=yB=2.

因为OC=CA，

所以yA=2yC=4.

（2）方法1：如图9，过点A作AE⊥Ox，垂足为点E，交BC于点F.

因为yC=2，

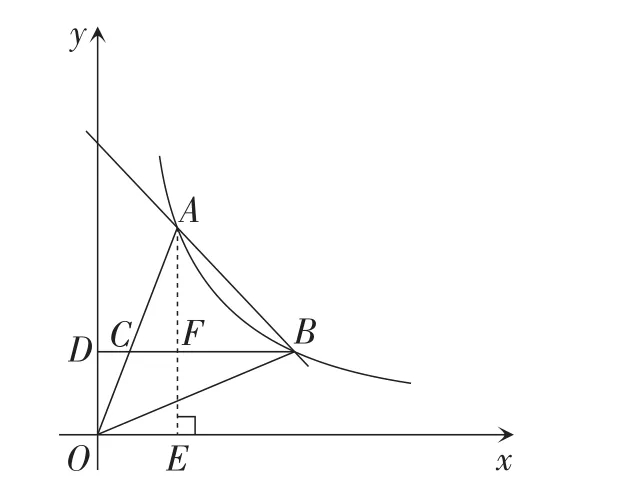
图9

【评析】借助直线OA的解析式确定点C的坐标，从而确定底边BC的长度，为表示△AOB的面积奠定基础.熟练确定三角形底边的高是解题的一个重要技巧，能熟练求解平行x轴的直线上两点间的线段长等于右侧点的横坐标与左侧点的横坐标的差是解题的关键之一.

方法2：如图10，过点A作AE⊥Ox，垂足为点E，交BC于点F，交OB于点G.

因为点B(3，2)，

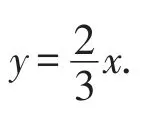
所以yG=1.

所以AG=yA-yG=4-1=3.

图10

【评析】借助直线OB的解析式确定点G的坐标，从而确定底边AG的长度，为表示△AOB的面积奠定基础.能熟练求解平行y轴的直线上两点间的线段长等于上侧点的纵坐标与下侧点的纵坐标的差也是解题的关键之一.

方法3：如图11，过点A作AE⊥Ox，垂足为点E，交OB于点G，过点B作BH⊥Ox，垂足为点H.

所以S△AOE=S△BOH.

所以S△AOG=S四边形GEHB.

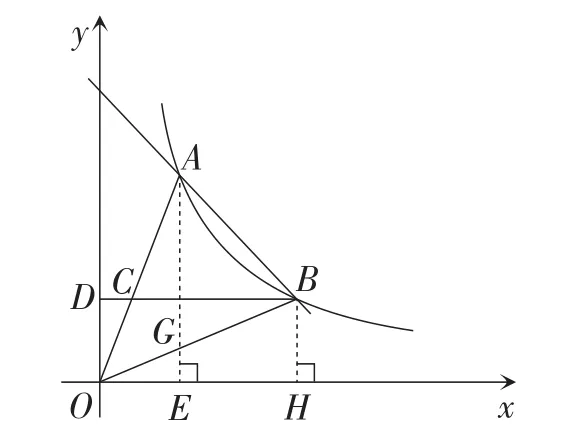
图11

【评析】利用反比例函数的性质把三角形的面积转化成与之相等的梯形面积也是求三角形面积的有效方法之一，要熟练掌握，并灵活运用.

方法4：如图12，过点A作AF⊥Oy，过点B作BE⊥Ox，垂足分别为点F，E，且两直线交于点G，

则四边形GFOE是矩形，且面积为12.

图12

【评析】把所求三角形面积通过补形法置于某矩形中，而矩形面积可求，其余生成的三角形面积也可求，故而△AOB面积可求，这也不失为一种高效的解题思路，值得借鉴.

方法5：如图13，过点A作AF⊥Oy，垂足为点F，过点B作BE⊥Ox，垂足为点E，证明略.

图13

此题所求三角形是反比例函数图象问题中经常出现的一个重要的三角形，求此三角形的面积往往是试题的一个重要知识选项，若能熟练掌握上述求解方法，再次遇到这样的问题，完整解答应该不是问题.

（3）根据函数解析式求面积.

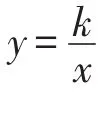
（1）求点A的坐标及双曲线的解析式；

（2）点B是双曲线上一点，且点B的纵坐标是1，连接OB，AB，求△AOB的面积.

图14

分析：利用直线与反比例函数的交点坐标的意义可以确定点A的坐标，继而确定反比例函数的解析式，也就确定了点B的坐标，进而把所求三角形的面积表示成矩形的面积减去另外三个直角三角形的面积即可求解.

解：（1）把x=1代入y=3x中，得y=3.

所以点A的坐标为A(1，3).

所以点B的坐标为B(3，1).

如图15，过点A作AC⊥Oy，垂足为点C，过点B作BD⊥Ox，垂足为点D，两直线交于点E.

根据题意，得OD=CE=3，OC=DE=3.

所以AE=EB=2.

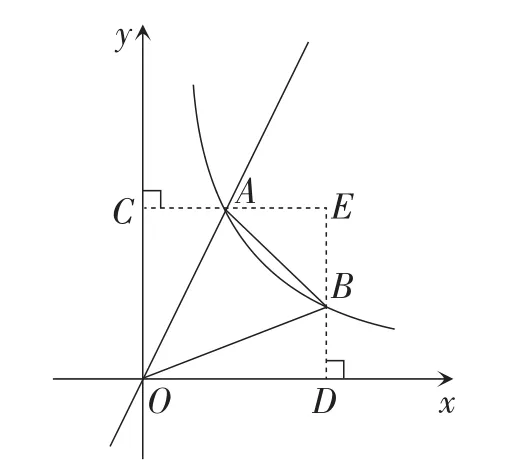
图15

【评析】构造矩形是解题的一种有效的解题思路，要熟练掌握.此外，熟练掌握反比例函数k与三角形面积的关系也是成功解题的一个重要因素.

根据题意学会构造反比例函数图象上一点的矩形，使用k的几何意义为解题奠定基础，这是需要灵活掌握的有效方法之一.