利用信息技术进行数学探究
——以“一次函数的图象与性质”为例
蒋 跃
(安徽省淮北市袁庄实验学校)
函数是研究现实世界变化规律的一个重要模型,是中学数学的核心内容,函数知识具有高度的抽象性,对初中生来说是学习上的一大难点.一次函数的学习对学生形成函数思想,对后续函数的学习,对学生数学核心素养的提升,都是非常重要的.利用信息技术可以使抽象的学习内容形象化、直观化、动态化地呈现在学生面前,从而有效突破函数学习的难点.下面以泸科版《义务教育教科书·数学》八年级上册(以下统称“教材”)第十二章第2节“一次函数”(第2课时)“一次函数的图象与性质”的教学为例,谈谈如何利用信息技术进行数学探究,发展学生的几何直观,助力直观想象,提升数学核心素养.
一、由点成线,直观想象函数图象
一次函数的图象是一条直线,而线是由点组成的.教材通过描出五个点,并与正比例函数进行对比,得出一次函数的图象是一条直线.这样处理,学生或许能理解“一次函数的图象是一条直线”,但不一定信服.教学中,教师可以借助信息技术强大的数据处理和绘图功能,描出尽可能多的点,让学生通过观察,发现这些点组成了什么图形,然后通过直观想象,得出函数的图象,使学生信服一次函数的图象的确是一条直线.
例如,画一次函数y=2x+1的图象.
如图1,利用几何画板软件列表、描点,先描出6个点,让学生观察这些点所组成的图形.由于点的数目较少且分散,学生不易观察出这些点组成了什么图形,但应该能直观感知到这些点大致分布在一条直线上.

图1
如图2,增加点的数目,继续描点,观察这些点所组成的图形.随着点的数目增多,相邻两点之间的距离变小,点的密度变大,学生会直观认识到这些点可能会组成一条直线.
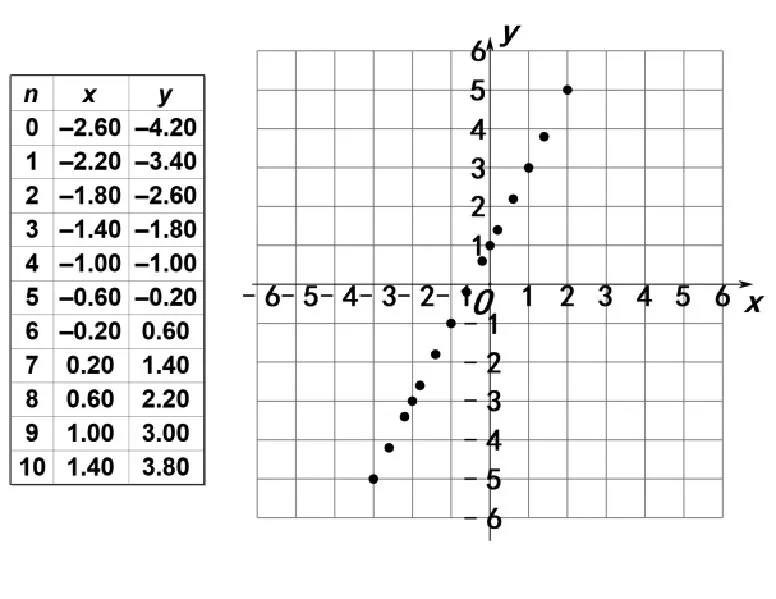
图2
如图3,增加点的数目,继续描点,再让学生观察这些点所组成的图形.随着点的数目增多,点越来越密,学生便可观察出这些点组成了一条直线.

图3
教师进一步追问:通过观察这些点组成的图形,你能想象出一次函数的图象是什么形状吗?
学生可直观想象出一次函数的图象是一条直线.
最后,教师总结:根据两点确定一条直线,画一次函数图象时,只要先描出两个点(一般选择两个特殊的点,即直线与坐标轴的两个交点),再过这两个点画直线就可以了.一次函数y=kx+b(k,b为常数,且k≠0)的图象叫做直线y=kx+b.
【设计意图】通过几何画板软件不断描点,增加点的数目,使这些点组成的图形越来越接近直线,易于学生直观感知一次函数图象的形状,有助于发展学生的几何直观,培养学生的直观想象能力.
二、数形结合,直观感受函数性质
史宁中教授曾说:数学知识的形成依赖于直观,数学知识的确定依赖于推理.也就是说,在多数情况下,数学的结果是“看”出来的,而不是“证”出来的,所谓的“看”就是直觉判断.在探究一次函数的性质时,把点的坐标与点在平面直角坐标系中的位置相结合,让学生观察图形,通过直觉判断函数性质,然后再通过例子进行验证,有利于学生几何直观能力的发展.
仍以一次函数y=2x+1为例.教师提出如下问题.
问题1:如图4,观察图中的表格,随着自变量x的变化,函数y发生什么变化?
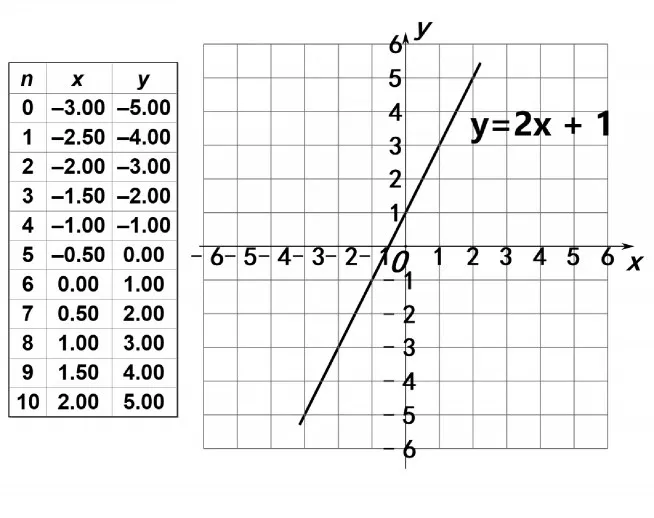
图4
学生不难看出,y随x的增大而增大.
问题2:观察函数的图象,从左向右,图象有什么变化?
学生可以看出,从左向右,此函数图象是上升的.
追问1:改变k(k>0)的值,刚才得到的结论是否会发生变化?
此时教师留给学生思考的时间,然后找学生回答,最后教师利用几何画板软件演示验证.
追问2:如果k<0,函数图象有什么性质?
学生回答过后,教师利用几何画板软件验证,最后师生总结得出一次函数的如下性质:当k>0时,y随x的增大而增大,函数图象是自左向右上升的;当k<0时,y随x的增大而减小,图象是自左向右下降的.
【设计意图】通过观察表格和函数图象,继续发展学生的几何直观,渗透数形结合思想.通过教师提问,学生思考并回答,提升学生的直观想象能力.
三、化静为动,直观体验图形变化
教材上的知识都是以静态的方式呈现的,而现实世界一个相对变化的、动态的世界,我们学习的知识也是如此.一次函数y=kx+b(k,b为常数,且k≠0)的图象会随着系数k,b的变化而变化,但传统的课堂教学是静态的,这使得学生习惯用静态的思维方式思考问题,从而造成学习上的困难.而利用信息技术,就能把研究对象动态的呈现出来,从而引起学生思维方式从静态向动态转变,用动态的思维想象函数的变化,突破学习难点.
问题3:一次函数y=kx+b(k,b为常数,且k≠0)的图象与系数k,b之间存在什么关系呢?
b的关系学生较好理解,因为当x=0时,y=b,所以b就是一次函数图象与y轴交点的纵坐标.因此b决定了一次函数图象与y轴交点的位置,b叫做直线y=kx+b在y轴上的截距.而k与函数图象的关系比较复杂、抽象,学生难以理解.教师可以利用几何画板软件,把k用参数加以设置,然后通过k的连续变化,观察图象的变化,化静为动,直观体验图象的变化,如图5、图6所示.

图5

图6
通过动态演示,学生可直观体验到k的值与函数图象之间的关系,k的符号决定了函数图象自左向右是上升的还是下降的,即图象的倾斜方向;k的绝对值决定了函数图象是靠近x轴还是y轴,即图象的倾斜程度.
【设计意图】通过几何画板软件的动态演示,可以看出函数图象随着系数的变化情况,使抽象的研究对象形象化、动态化,增加学生的直观体验,发展学生的动态思维能力,提高学生的学习兴趣,突破知识难点.
问题4:一次函数y=kx+b的图象与正比例函数y=kx的图象有什么关系?
问题5:对于直线y=k1x+b1与直线y=k2x+b2,当k1,k2,b1,b2有什么关系时,两直线相交、平行、重合?
学生思考后回答,并试着说明理由.教师根据学生的回答情况进行及时点拨.可以从函数图象的角度进行直观想象,再从系数k,b与一次函数图象关系的角度进行说理,然后教师利用几何画板软件进行验证.
【设计意图】通过问题引发学生思考,发展学生的空间想象能力和逻辑思维水平,培养学生利用直观想象解决问题的能力,提升数学核心素养.
函数知识抽象性较强,而八年级学生抽象思维能力还比较弱,抽象思维还依赖于感性经验的支持,从而使学生的学习产生了困难.八年级学生已经具备一定的观察能力,能按照教学要求有意识地进行观察,但深入性不够,不能透过复杂的现象看本质.教师在设计教学活动时要考虑学生的认知特点,充分利用信息技术,创造性地设计教学活动,尽可能地把抽象的问题直观化、形象化、动态化地呈现给学生,为学生发现、探究和解决问题提供传统教学手段很难提供的学习和研究环境,促进信息技术与数学学科的融合,发展学生的几何直观,助力直观想象,提升学生的数学核心素养.

