“怎样解题表”在解题教学中的运用
杨运标
(广东省东莞市中堂镇实验中学)
一直以来,不少教师在解题教学方面存在着弊端.有些教师在解题教学时总停留在简单的小结、归类上,缺乏数学思想上的归纳,讲解题目时只是说“我们这样解”,而不是说“为什么这样解,这样做经历了怎样的思考全过程”.我们要教学生学解题,这就不仅仅是解题教学,更不是纯粹的解题,关键是在于学生的“学”.解题不仅是求解,更是思维过程的揭示;解题不仅仅是寻找答案,更需要自觉分析;解题分析不仅仅是数学学习的方法,更是一种理念.
数学教育家波利亚在《怎样解题》一书中给出了解题的思路,给出了程序化的解题系统.下面笔者就结合一道中考模拟题,来谈谈波利亚的“怎样解题表”在数学解题教学中的运用.
一、波利亚的“怎样解题表”
第一步:你必须弄清问题.
未知、已知、条件分别是什么?满足条件是否可能?要确定未知,条件充不充分?
第二步:找出已知数与未知数之间的联系.如果找不出直接的联系,你可能不得不考虑辅助问题.你应该最终得出一个求解的计划.
你以前见过它吗?你是否见过类似的问题?你是否知道与此有关的问题?你是否知道一个可能用得上的定理?这里有一个与你现在的问题有关,且早已解决的问题,你能不能利用它?为了利用它,你是否应该引入某些辅助元素?你能不能重新或换个方法叙述这个问题?回到定义去.如果你不能解决所提出的问题,可以先解决一个与此有关的问题.你能不能想出一个更容易着手的有关问题?尝试弱化条件.这样对于未知数能确定到什么程度?
第三步:实行你的计划.
实现你的求解计划,检验每一步骤.你能否清楚地看出这一步骤是正确的?你能否证明这一步骤是正确的?
第四步:验算所得到的解.
你能否检验这个论证?你能否用别的方法导出这个结果?你能不能一下子看出它来?你能不能把这个结果或方法用于其他的问题?
二、对“怎样解题表”的理解
1.理清题意,学会审题
波利亚用一连串的自我提问表单来教我们如何正确审题,如何弄清问题.学会用数学语言或符号把问题重新叙述一遍,这是数学思想中的转化思想,目标是要写出形式化的数学表达式.
2.拟定计划,暴露解题分析的思维全过程
波利亚《怎样解题》一书中最精彩的就是在教我们如何解题,应该如何思维,且把思维的总过程呈现出来.在“怎样解题表”中用一系列的认知提问和元认知提问来剖析问题结构.例如,(1)回想:你是否见过相同的问题而形式稍有不同?(2)联想:看着问题,试想出一个具有相同性质的问题或相似情况的熟悉的问题.
我们教学生学解题,先要向学生暴露自己完整的思维过程,包括教师深入思考时所经历到的曲折或错误,让学生知道教师在遇到困难或阻力时是如何思考前进的,如何检验和修正方案的,这是一种解题分析的示范,有利于学生形成正确的解题观.
3.实现计划,规范书写过程
解题主体按照拟订的解题计划与程序,实施变换、运算、推理、作图,从而得到问题的解.在这一步骤中,波利亚提醒我们要注意运算的合理性,作图的准确性,逻辑推理的严密性,以及表达的条理性和规范性.
4.回顾反思,提升能力
波利亚的问题表单:你能否检验这个论证?你能一题多解吗?你能不能一下子看出它来?你能不能把这个结果或方法用于其他的问题?可以看出这一步是解题的必要程序,体现了检验、回顾、引申、拓展的作用.
三、“怎样解题表”的实践研究
1.问题引入
题目如图1,在平面直角坐标系中,已知二次函数y=ax2+bx+c(a≠0)的图象经过A(-1,0),B(3,0),C(6,4)三点.
(1)求此二次函数解析式和顶点D的坐标;

②若抛物线对称轴上点H到直线BC的距离等于点H到x轴的距离,则求出点H的坐标;

图1
2.根据波利亚“怎样解题表”进行解题分析
将上述题目的问题按照波利亚“怎样解题表”的四个步骤来进行分析.
(1)第(1)小题.
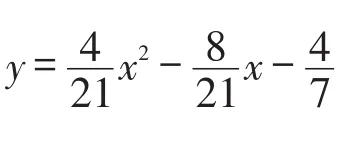
(2)第(2)小题第①问解题思路分析.
第一步:理清问题.

问题:求点E的坐标.
第二步:拟订计划.


第三步:实现计划.

整理得4x2-8x-12-21t=0.
第四步:回顾.

(3)第(2)小题第②问解题思路分析.
第一步:理清问题.
已知:抛物线对称轴上点H到直线BC的距离等于点H到x轴的距离.
未知:求出点H的坐标.
第二步:拟订计划.
如果你很难直接找到条件与问题之间的关联,就先考虑一些辅助问题,你是否知道与此有关的问题?求一个点的坐标常用方法是解析法和几何法.首先考虑几何法,如图2,由角平分线的性质可以构造一对全等三角形,但是等量关系较难建立起来,不知道如何列出方程,故暂不考虑几何法.
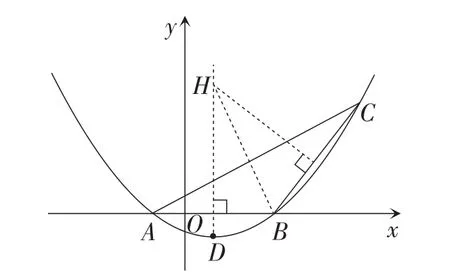
图2
利用解析法又该如何做呢?你能不能换一种方式重新表述这个问题?你能不能用不同的方法重新叙述它?根据到两边距离相等的点在它的角平分线上,联想到点H是∠ABC的平分线与抛物线对称轴的交点,我们已经知道了抛物线对称轴的方程为x=1,只要再知道∠ABC的平分线BH的解析式就可以了.
求直线表达式需要两个确定的点,所以除了已知的点B以外,还需要一个点.你是否知道与此有关的问题?知道一个可能用得上的定理?由角平分线联想到等腰三角形、三线合一,从而有中点,故创设辅助条件构造一个等腰三角形.明显△ABC不是等腰三角形,可求得BC=5.在x轴上取点R(-2,0),则有RB=5.所以BC=RB=5.利用中位线定理或中点坐标公式可得其中点坐标(2,2),该点就是BH上的确定点,从而问题得到突破.
第三步:实现计划.
简解:如图3,作∠ABC的平分线与对称轴x=1的交点即为点H.
在x轴上取点R(-2,0),连接RC交∠ABC的平分线BH于点Q,则有RB=5.
易得△RBC是等腰三角形,可求得过点B,Q的一次函数解析式为y=-2x+6.
当x=1时,y=4.
故点H的坐标为(1,4).

图3
第四步:回顾.
留意到题目表达用词“直线BC”,而题图看起来是线段BC,这样会不会漏掉解呢?如图4,如果延长CB,作∠ABF的平分线BH2交对称轴于点H2,此时点H2也符合题意,所以前面的分析不完善.虽然前面的思考我们没有完全成功,但是我们已经找到突破口,而且求得一解了.考虑到一对邻补角的平分线互相垂直及图3已经求得的H1(1,4),用相似的性质很快就可求得H2(1,-1).综上所述,点H的坐标是(1,4)或(1,-1).
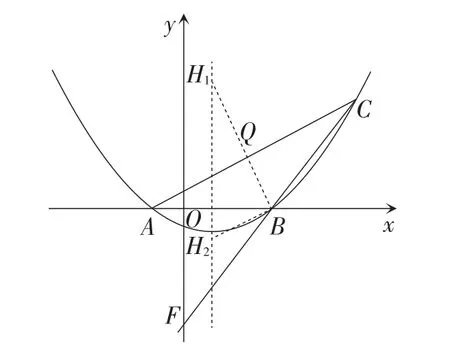
图4
(4)第(3)小题解题思路分析.
第一步:理清问题.
问题:是否存在一个定值λ,使得CJ+λ∙EJ的最小值是 26.若存在,求出λ的值;若不存在,说明理由.
第二步:拟订计划.

第三步:实现计划.

理由如下.
如图5,在对称轴上取点K(1,3),
又因为∠JIE=∠KIJ,
所以△IJE∽△IKJ.

则CJ+λ×EJ的最小值为 26.
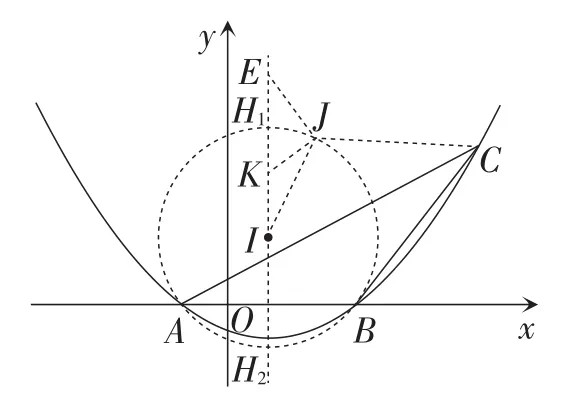
图5
第四步:回顾.
反思归纳“阿氏圆”模型的一般解题模式步骤.
问题历史背景:“阿氏圆”又称“阿波罗尼斯圆”,已知平面上两点A,B,则所有满足PA=k∙PB(k≠1)的点P的轨迹是一个圆,这个轨迹最先由古希腊数学家阿波罗尼斯发现,故称“阿氏圆”.
如图6,⊙O的半径为r,点A,B都在⊙O外,点P为⊙O上的动点,连接PA,PB,已知r=k∙OB,则当“PA+k∙PB”的值最小时,点P的位置如何确定?
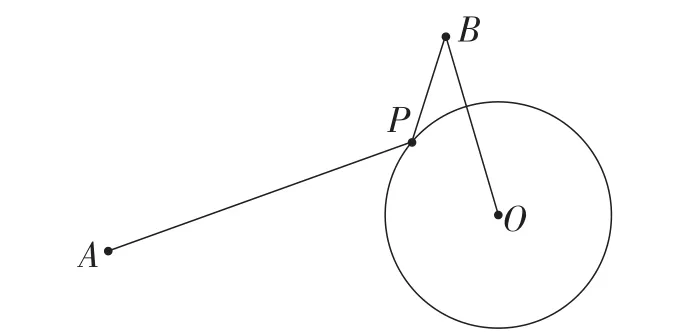
图6
①类型:“PA+k∙PB”型最小值.
②特征:动点P在圆上运动.
③原理:两点之间线段最短;
三角形的三边关系:两边之和大于第三边,两边之差小于第三边.
④方法:等效法.
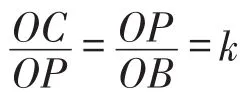

图7
从而有了“阿氏圆”数学模型一般化的解题步骤.
第一步:连线.将系数不为1的线段的两个端点分别与圆心相连接,即连接OP,OB.


第四步:求值.连接AC,与⊙O交点P即为取最小值时点P的位置,AC长即为最小值.
其实就是等效换边,把k∙PB转换成边PC,则PA+k∙PB=PA+PC,然后理解为定点A到动点P的距离加上动点P到定点C的距离,关键是要固定线段AC经过动点P所在圆,根据两点之间线段最短即可解决问题.
四、结束语
“怎样解题表”的自我提问表单是一种思路启发性的提问,而不是一种解题的固定模式,并非要涉及到表单中的每一个问题,而应该根据具体情况灵活运用,创造性地使用“怎样解题表”.不断地变换问题直至与已有的知识经验接轨,让问题变换到知识的最近发展区来,回到熟悉的问题上来.教师可以尝试用“怎样解题表”的自我提问表单进行解题教学,帮助学生在解题过程中理解题意、理清问题,进而找到问题解决的方法.并长期坚持下去,学生将逐步形成自己的提问表单,并在解题中加以应用,最终内化成一种能力,一种有效的思维模式.

