因“生”制“练”用“活”教材

范琰

摘  要：新教材关注学生获得知识的过程，注重探究能力和学习习惯的培养。笔者从教学实践中学生练习的难度来反观新教材，发现有些例题、习题的配置欠合理。教师在利用教材时，要有科学的教材解读观。深入研究编者意图的同时也要根据学情，因“生”制“练”，对例题与习题进行合理的布局、删减、增加、转换。使知识点的落实更富有张力，使之适合学生知识的掌握、框架的建构和能力的提升。

关键词：小学数学;例题;整体把握

教材是编者设置承载知识的一个载体。教师在运用教材时，要有科学的教材解读观。深入研究编者的意图同时也要根据学情，以生为本，因“生”制“练”。利用好例题与习题进行合理的删减、转换、增加。使知识点的落实富有张力，使之适合学生知识的掌握、综合解题能力的提升，从而提高教学质量。本文以五年级《植树问题》单元为例，谈谈在课堂教学中，例题与习题配置层次性、互逆性、沟通性、开放性等方面的适度把握。

一、由此及彼，拓宽思维，学法迁移由单一走向多元

课本例题所承载的是单一的知识点，有效的习题设计能让这个知识点向着各个方向辐射。很多学生由于思路闭塞无法真正拓宽思路，这正是因为他们联想的羽翼不够丰满。他们总是孤立地看待问题，而没有由此及彼地寻找问题间的本质联系。这种“思接千载”“视通万里”的联想能力也需要在课堂上加以锻炼。从而使我们的学法迁移由单一走向多元。例如：

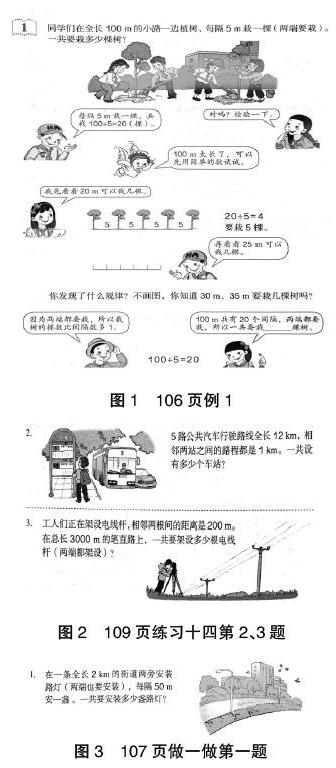
在讲解完例题1后，整合了图2练习十四第2、3题和图3做一做的第一题。教师把三个题组一起，让学生先读题，留足时间让他们思考。

师：这三道题有什么共同之处吗？它们和例题有什么联系吗？

在读完题停留30秒后，留给孩子思考的空间。有孩子举手说：“我觉得这三道题属于植树问题两端都栽的情况。”

师：“你能说说想法吗？那相当于求什么呢？”

生：“相当于植树问题里的树。如第2题中，可以把12千米看作植树的总长，相邻路程1千米看作植树的间隔距离，求多少个车站就看作求植树的棵数。”

当学生如此清晰地表达习题与例题的相似点时，题组的练习目的也就达到了。学生能由此及彼，由例题的学习想到习题的拓展，清晰地建立起关系，做到真正的沟通联系、举一反三。

二、化静为动，拾级而上，解题能力由模仿走向创造

教材中的例题与习题是静态呈现的。它只是为知识的传递提供了可能。但是我们的课堂教学是活的，是富有生命力的。如何运用化静为动，为我们的教学提供更多灵动的素材，这就需要我们的教师有一颗深究的心和科学的教材观。教材的呈现方式是静态的，有些看似简单的教学内容，往往蕴藏着丰富的数学内涵，这时就需要教师针对内容的特点和学生的实际情况去深挖和拓展。例如：

2. 小红要给一块长48厘米、宽36米的长方形的四周绣花。她每隔6厘米绣一朵花，四个角上个绣上一朵花，那么她一共要绣多少朵花？

3. 圆形的跑道插着100面小旗，两面小旗的间隔是4米，如果现在想插80面，间隔应为多少米？

在例题3的学习之后，笔者安排了3道层次丰富的习题。第一题是课本111页12题，这题只是知识的迁移，由种树问题演变成求项链上的水晶，同类型便于学生沟通。对学生来说是例题的变式，难度不大。第二题让学生独立完成，对于中下以上的学生，感觉有点困难，而好的学生的适时点拨，就能让他们恍然大悟。重在沟通长方形、正方形等也是属于封闭图形，和圆形异形却同理。第三道练习突破求植树问题中的棵树模型，是对这种数学模型的综合运用，已知小旗的面数和间隔距离，根据面数与间隔数相同，可以求出跑道的总长，再根据改后只插80面，可以求出改后的间隔长度。

学生接触新知识，对知识的掌握是一个循序渐进、螺旋上升的过程。它靠慢慢地累积、不断地对比、仔细地甄别来完成对新知识的建构。有层次的练习题正是学生完成这种构建的载体，它能不断在学生的“最近发展区”的基础上对知识进行逐步的提炼、建模、深化。

三、由顺而逆，适时转换，思维能力由机械走向灵活

传统教育以正向思维为主，导致学生解题中思路僵化，模式化明显，不能灵活地应用知识。在实际教学中，通过对学生进行逻辑性较强的逆向思维的引导，让学生从不同的角度思考问题，摆脱思维定式，加深对知识的理解。所以适时将练习进行逆向转换，由正及反，正反并举，引导学生思维的逆向思考，使学生的思路更加灵活、深刻。例如：

2. 从教学楼到食堂有一条笔直的通道，通道的一边种了44颗樟树，相邻两颗樟树的距离是5米，从教学楼到食堂有多远？

在教学了例题2后，笔者安排了2道练习题。第一题来自109页练习十四第6题，第二題来自课堂作业77页第5题，整合了两道互逆的练习题。

在第一题的安排上，抓住知识的连接点，利用例题与习题的关系，顺势而导。学生根据经验自主加工构建。而第二道练习，抓住知识的生长点，通过已经种了的44棵樟树，可以求什么？又根据教学楼和食堂相当于植树问题中的两端都不种，可以反过来求出间隔数就是55个。这样把学生思维由正面带向反面，理清学生的思路，理顺对关系的思考与理解。教师应充分培养学生的双向思维能力，学会从不同角度看问题，提高学生思维的品质。

四、由点到面，补齐知识，认知结构由平面走向立体

数学教材是数学知识体系的阶段反映。各例题之间的相互融合成就了一种数学思想。课本的例题往往只是一个知识点呈现，而习题的安排有可能就是知识点的补充或是对应的知识点。那么零散的知识点如何成为一条条知识链，一条条知识链又如何形成一个个知识面呢？这就需要我们教师站在一个制高点上去审视和把握教材，学会正确处理习题的关系，必要时对有些习题进行颠三倒四，适时整合;把典型习题处理得厚重一些，厚此薄彼;甚至可以像教学例题那样详尽，以此来补齐学生的知识断面。例如：

1. 同学们军训，站成方队的最外层每边站了16个，最外层一共有多少名学生？

2. 同学们站成方队进行军训，知道最外层一共站了68人，那么最外层每边站了多少人？

课本111頁练习二十四第14题并不是一道例题，而是一道普通的习题。但它是一个重要的知识点，是一种典型问题。我们教师在处理它时不能一笔带过，而是浓墨重彩。我们不仅要花足够多的时间帮助学生理清数量关系，还要融会贯通它的变式题，把一个个潜在的知识激发出来，以此补齐知识断面，向学生传递一个完整的数学模型，帮学生建立一个融会贯通的网状知识结构。

五、由表及里，沟通联系，知识结构由孤立走向系统

在点状的例题知识学习之后，教师可以把每个知识点进行巧妙融合，放置到更广阔的背景下“联结”。这不仅能有效盘活知识间的联系，而且有助于学生多角度地理解知识，综合地分析和应用知识，悟到数学知识内部间的融合关系，使知识结构由孤立、无序走向系统、完整。例如：

A、为迎接“六一”儿童节，学校准备在8米长的主席台上放盆花（两头都不放），每相邻的两盆盆花之间的距离是50厘米，那么学校需要准备多少盆盆花？

B、丁丁在练习滑轮绕桩时，一共放了20个桩，每两个桩之间的距离是80厘米，那么首尾两个桩之间的距离是多少米？

C、公园正门正对的一条笔直的公路长120米，现要在公路两边种梧桐树，每两棵树相距6米。园林工人共需要准备多少棵树？

在教学完三个例题的练习课中，笔者安排了让学生解答ABC三道练习题。先让学生进行独立解答，再同桌进行交流，在反馈完3道题目之后，课件显示出植树问题的三个例题。让他们找找看三道题目与三个例题的联系。给他们足够多的时间思考。

生：我觉得A和例题2可以归为一类，B和例题1是一类，而C又和例题3归为一类。

师：说说你的看法，为什么属于一类？

生：A题和例题2都是属于两端都不种的植树问题，B题和例题1是属于两端都种的植树问题，而C题和例题3属于只种一端的植树问题。

师：这两组题目有什么区别吗？

生：有区别的，例如B题和例题1虽然都属于两端都种的植树问题，但是例题1是已知总距离和间隔距离求棵树，而B题就相当于植树问题里的已知棵数和间隔距离求总距离。

整节练习课目标的制定与教学过程的展开紧密相连，环环相扣。教学过程的展开就为目标的达成服务，围绕着学生对知识的整理和构建模型的完成。由习题引回例题，比较题组与3个例题的联系和区别。以学生的观察能力、探究能力和学生的合作能力为主要目标，为学生对单元知识点的建构搭建了一个合理的支架;沟通知识之间的本质联系，使学生构建起完整的单元知识的立体框架。

教材是学生学习数学的第一手资料，是传递知识点的载体。正确的教材观绝不仅仅止于如何“用教材教”，同时应该倡导动态、立体、丰满、灵动充满文化张力的科学的教材解读观。我们一直相信，教材是静态的，但是编者、教师、学生是有着火热生命的。每一张静默的图片背后可能蕴含着丰富的数学思想，每一个简单的算式深处可能饱含着火热的数学思考。教材并不是枯燥乏味的，而是生动活泼的;不是“线性静止”的，而是“立体灵动”的。