巧用向量等和线 求解一类高考题

张玉虎

[摘  要] 平面向量是高中新课标教材新增的重要内容，是有效连接代数与几何的桥梁，已经成为高考数学命题的一个热点，向量等和线为求解向量系数和问题打开了一种崭新的解题空间，体现出考生的良好学科素养.

[关键词] 向量;等和线;高考题

平面向量是新课标教材新增内容之一，具有有效沟通代数和几何的桥梁作用，向量也是人们解决数学问题的一种重要数学工具. 在高考数学中向量既是一个必考知识点，也是一个创新命题的切入点，考题常考常新，而且在近几年的考题中对知识的综合性和灵活性考查增强，相应难度有所提升，如2017年全国卷Ⅱ、全国卷Ⅲ，向量题就被安排在选择题的第12题.因此，教师在指导学生对平面向量进行复习时，要重视回归教材，指导学生对教材中向量的定理、例题、习题展开适当的探究与思考，以拓展知识和能力，其中从平面向量基本定理探究出的向量等和线就是一个重要例子，利用向量等和线求解向量线性运算中系数和问题，比建系转化为代数问题来求解更显自然和流畅，有效降低了知识综合性要求与运算能力要求.

[?]向量等和线定理的探究

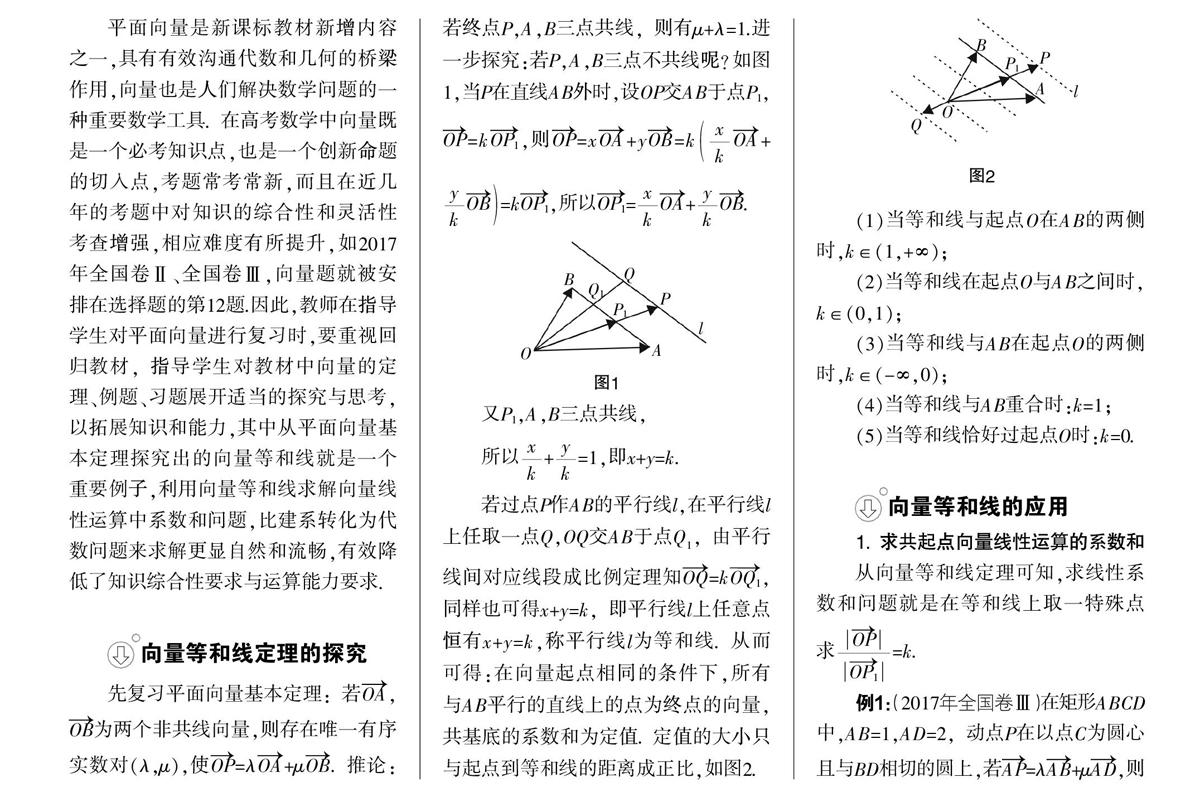
若过点P作AB的平行线l，在平行线l上任取一点Q，OQ交AB于点Q，由平行线间对应线段成比例定理知=k，同样也可得x+y=k，即平行线l上任意点恒有x+y=k，称平行线l为等和线. 从而可得：在向量起点相同的条件下，所有与AB平行的直线上的点为终点的向量，共基底的系数和为定值. 定值的大小只与起点到等和线的距离成正比，如图2.

（1）当等和线与起点O在AB的两侧时，k∈（1，+∞）;

（2）当等和线在起点O与AB之间时，k∈（0，1）;

（3）当等和线与AB在起点O的两侧时，k∈（-∞，0）;

（4）当等和线与AB重合时：k=1;

（5）当等和线恰好过起点O时：k=0.

[?]向量等和线的应用

1. 求共起点向量线性运算的系数和

从向量等和线定理可知，求线性系数和问题就是在等和线上取一特殊点求=k.

例1：（2017年全国卷Ⅲ）在矩形ABCD中，AB=1，AD=2，动点P在以点C为圆心且与BD相切的圆上，若=λ+μ，则λ+μ的最大值为（  ）

A. 3 B. 2 C.D. 2

解析：如图3，作圆C与BD平行的切线l，设切点为P，

连接AP交BD于P1，则直线l为使λ+μ取得最大值的等和线，

此时==3，故选A.

例2：（2009年安徽卷）给定两个长度为1的平面向量和，它们的夹角为，如图4所示，点C在以O为圆心的圆弧AB上变动，若=x+y（x，y∈R），则x+y的最大值为________.

解析：在圆弧AB上过C点作AB的所有平行线中，当平行线与圆弧AB相切时离圆心最远，此时等和线的k取得最大值，结合圆心角可计算得kmax=2.

2. 求非共起点向量线性运算的系数和

由于高中阶段所学向量均为自由向量，把向量平移是相等向量，所以在用等和线求解问题时，若两向量的起点不同，可以将向量平移实现起点重合.

例3：（2013年江苏卷）设点D，E分别是△ABC的边AB，BC上的点，AD=AB，BE=BC. 若=λ1+λ2（λ1，λ2∈R），则λ1+λ2的最大值为________.

解析：如图5，过点A作=，延长AF与BC交于点M.

由于∥且点D为AB的中点，从而E也为BM的中点，

所以F也为AM的中点，可得DF∥BC，因此λ1+λ2=，也为最大值.

3. 求向量线性运算系数的线性关系式

有时候所求解的可能是系数的一般线性关系式，而非系数和，考虑到向量可以通过数乘运算将向量进行同向或者反向伸长、压缩，所以从理论上讲，所有系数的线性关系式，都可以通过改变向量的基底，将所求系数的线性关系式变为两个新的基向量的系数和.

求x+3y可转化为以，为基底的系数和. 如图6，当点C在点A处时，经过k=1的等和线;当点C在点B处时，经过k=3的等和线，这两个值就是等和线最近与最远的值，所以系数和k的取值范围为[1，3]，故选C.

4. 求基底为变化向量的系数线性系式

当基向量的终点是变化的，使系数和μ+λ=1的等和线也是变化的，所以满足条件的的等和线也相应保持平行变化，从而求解问题的关键在于探求保持平行变化中满足条件的等和线位置.

当点P在半圆弧AB上变化时，以，为基向量的值为1的等和線PD′相应发生改变，从而过E点的等和线EE′也跟随改变. 通过观察知当P运动到P′点时，值为1的等和线PD′与过E点的等和线EE′重合，此时2x+y的最小值为1，故选C.

[?]向量等和线的推广

与向量等和线相对应的还有向量的等差线、等积线和等商线，各自定义分别如下：

1. 向量的等差线

平面内一组基底，及任一向量，设=λ+μ（λ，μ∈R），点C为线段AB的中点，若点P在直线OC上或在平行于OC的直线上，则λ-μ=k（定值），反之也成立. 我们把直线OC以及与直线OC平行的直线称为向量的等差线，如图8.

2. 向量的等积线

平面内一组基底，及任一向量，设=λ+μ（λ，μ∈R），若点P在以直线OA，OB为渐近线的双曲线上，则λμ=k（定值），反之也成立. 我们把以直线OA，OB为渐近线的双曲线称为向量的等积线.

3. 向量的等商线

平面内一组基底，及任一向量，设=λ+μ（λ，μ∈R），若点P在过O点（不与OA重合）的直线上，则=k（定值），反之也成立.

我们把过点O的直线（除OA外）称为向量的等商线，如图9.

对直线OC上任意一点都恒为定值，不妨过点A作AC1∥OB交OC于点C1，再过点C1作B1C1∥OA交OB于点B1，由已知可得AC1=OB1=，从而=+=+，即此时m=1，n=.

所以定值=3，故选B.

从以上对历年向量高考题的解题分析可以看出，向量的等和线巧妙地将代数问题转化为图形关系问题，将系数和的代数式运算转化为了距离的比例运算，数形结合思想得到了有效直接的体现. 向量的等和线法将复杂的不等式问题、范围问题、数量积问题转化为简单、直接、操作方便的点到直线距离问题，很多时候用相似即可迅速解决，提高了做题时间效率和正确率，提升了学生的学习热情和学习兴趣，也是素养立意的高考命题原则的体现.