多重高斯有向图模型结构学习

王 琦 赵 强

( 山东师范大学数学与统计学院，250358，济南 )

1 引 言

当图模型中节点表示高斯随机变量的时候，随机变量之间的条件独立性可以通过高斯随机变量的逆协方差阵中的零元素反映.因此，估计高斯无向图等价于估计随机变量的逆协方差阵.近年来，已经有大量的算法相继被提出用于估计高斯无向图.Meinshausen[1]通过节点之间的相关性建立回归模型，考虑到节点关系的稀疏性，使用 Lasso 惩罚项估计稀疏的逆协方差阵并证明了该算法在一定条件下的高恢复率.在文献[2]、[3]和[4]中，根据逆协方差阵的极大似然估计模型，在不同的数据背景下基于不同的惩罚项估计逆协方差阵，在数值模拟和真实数据两种情况下均取得了较好的效果.在大数据时代，某些时候需要对多个高斯无向图进行联合估计.Guo[5]等提出了一种带有阶级化惩罚项的极大似然估计模型，该惩罚项的作用是为了使得多重图中具有相关性的节点同时展现出有边或者无边的性质，从而降低了算法的可行解空间.Zhu[6]、Danaher[7]和Ma[8]等人针对高斯多重图模型的联合估计提出了不同的惩罚项，比如:group Lasso，fused Lasso 等等.

当一个贝叶斯网络中的随机变量具有自然偏序先验的时候，估计贝叶斯网络就转换为估计贝叶斯网络的框架.这也就极大地降低了估计贝叶斯网络的复杂度.对于带有偏序先验的高斯有向图模型, 文献[9]中，通过建立带有 Lasso 约束项的优化模型求解邻接矩阵从而用于估计高斯有向图.Yuan[10]等人建立多重高斯有向图的极大似然估计模型，通过 DC 算法和增广拉格朗日算法估计多重高斯有向图.

估计多重高斯图的时候，不同高斯图之间往往具有相似性结构.充分利用不同图节点之间的相关性，能够降低优化问题的病态程度.因此，假设K重高斯有向图之间具有相似性结构，每一个高斯有向图有p个节点，每一个图分别有nk,k=1,...K次观测，在自然偏序先验条件下，本文建立了带有组相似性结构的极大似然估计模型，充分利用组相似性结构的先验信息构建惩罚函数，从而降低了高维数据中的解的可行空间，本文利用坐标下降方法求解该优化模型并得到了较好的高斯有向图估计.该算法的时间复杂度为O(max(nk)Kp2).数值实验展示了该算法估计多重高斯有向图的有效性.本文能充分利用图之间的相关性，联合估计出更加精确的高斯有向图模型结构.

本文的结构如下，第二节将介绍基本知识和带有自然偏序的隐变量模型，第三节将介绍高斯有向图模型和本文的算法，第四节为数值实验，最后是总结与展望.

2 基本概念和基础知识

2.1基础知识考虑一个图模型G=(V,E),其中V为图中节点，节点个数为p.E⊂V×V,为图中节点的边集.每一个节点都代表了一个随机变量X1,…，Xp，Xi和Xj是否有边代表两个节点是否有联系.有向边指的是如果(i,j)∈E, 那么(j,i)∉E.而无向边指的是如果(i,j)∈E,那么(j,i)∈E.对于有向图或无向图，如果在图模型中不能形成回路，则该图模型称为无环图.本文所讨论的图均为无环图.在图模型中,Pai指的是节点i的父节点所组成的集合，如果j∈Pai,记作j→i.有向图的框架指的是将有向图中的有向边换为无向边.通常用邻接矩阵A∈Rp×p表示边集E的条件相关性, 如果Aij=0, 则意味着Xi和Xj条件独立.

2.2自然偏序的隐变量模型在贝叶斯网络中，当节点具有自然偏序，即边的方向只能由序号低的节点Xi指向序号高的节点Xj(i>j). 此时，对于随机变量的因果推断通常用结构等式模型进行说明[11]:

Xi=fi(Pai,Zi)，i=1,…，p，

(1)

其中，Zi为Xi的隐变量.为了建立节点Xi之间的联系，本文讨论fi是一个线性函数，从而得到下列等式：

(2)

其中，ρij表示的是Xj节点和Xi节点的相关系数.当Xi,i=1,...,p服从高斯正态分布的时候，(1)和(2)等价[11].(2)式可以写成矩阵向量形式，X=ΛZ,其中Λ为影响矩阵，X∈Rp,Z∈Rn.举个例子，考虑图1中的高斯有向图，其影响矩阵Λ∈Rp×p,如(3)式所示.

(3)

图1 有向图

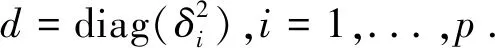
3 高斯有向图模型

3.1带惩罚项的高斯有向图考虑数据矩阵∈Rn×p是由(2)中的隐变量模型所生成的，不失一般性，假设Xi～N(0,1),Ω=Σ-1为逆协方差阵，对于Ω的极大似然估计表示如下[1]:

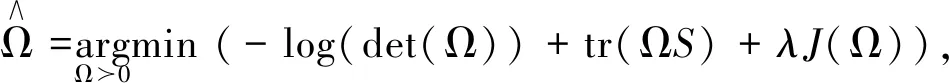
(4)

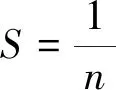
(5)

3.2多重高斯有向图估计假设有K个高斯有向图，从每个图中得到一个观测数据k∈Rp×nk,k=1,...,K，因此，依据(5)式，针对K个图的联合估计可以表达为:

(6)

对每一个K分别求取邻接矩阵Ak，从而可以估计出K个高斯有向图.考虑到在实际中，这些图之间会有已知的相似性结构，在优化函数中加入相似性结构的约束进行联合估计能够提高估计的准确度.优化模型如(7)，所示:

(7)

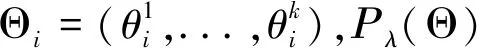
(8)

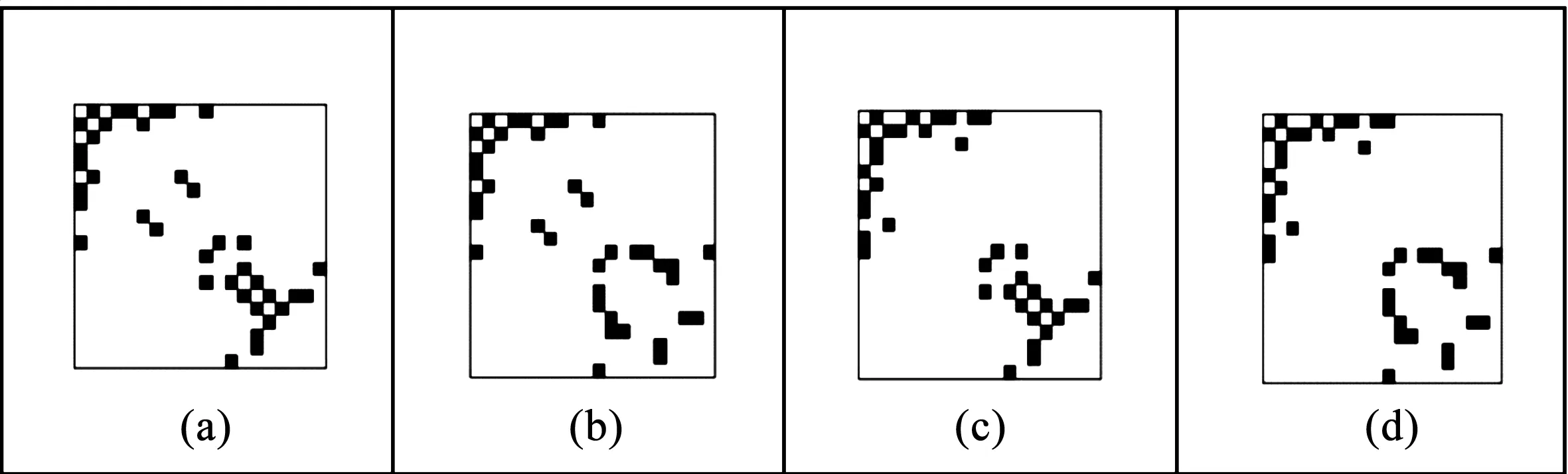
图2 四个高斯无向图的邻接矩阵

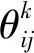
(9)

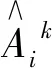
表1 算法1：多重高斯有向图联合估计

在实验中，需要对参数λijs进行估计.有两种方法可以对λijs进行估计.第一，根据已知的先验信息，对每一个三元组(i,j,s)选择特定的参数λijs.第二，对所有的λijs选取同一个λ作为参数. 在数值实验中，本文主要按照第二种方式进行参数选择.相比于CV方法和AIC方法，使用BIC方法进行参数选择在本数值实验中会有较好的效果.

4 数值实验

本节将通过数值实验验证算法1在估计多重高斯有向图的有效性.数值实验中有两个高斯有向图，每一个图中均有50个节点.高斯有向图的生成方法：首先建立一个相似性结构(图3)，即以0.009的概率在一个50×50的无边图上按照偏序先验进行加边.然后，对这个相似性结构分别随机地加边，最终使得加边得到的两个图的边的数量约为61.

根据生成图的邻接矩阵，按照文献[12]引理2.1中等式就可以计算得到两个高斯有向图的协方差阵.根据高斯有向图的均值和协方差阵，对两个图分别生成5 000个观测值.利用算法就可以得到两个高斯有向图的估计.本实验也同样使用PC算法作为对比,结果如图3所示.

分别计算两种算法的FPR,FNR,CZ三种指标.这三种指标的定义为：

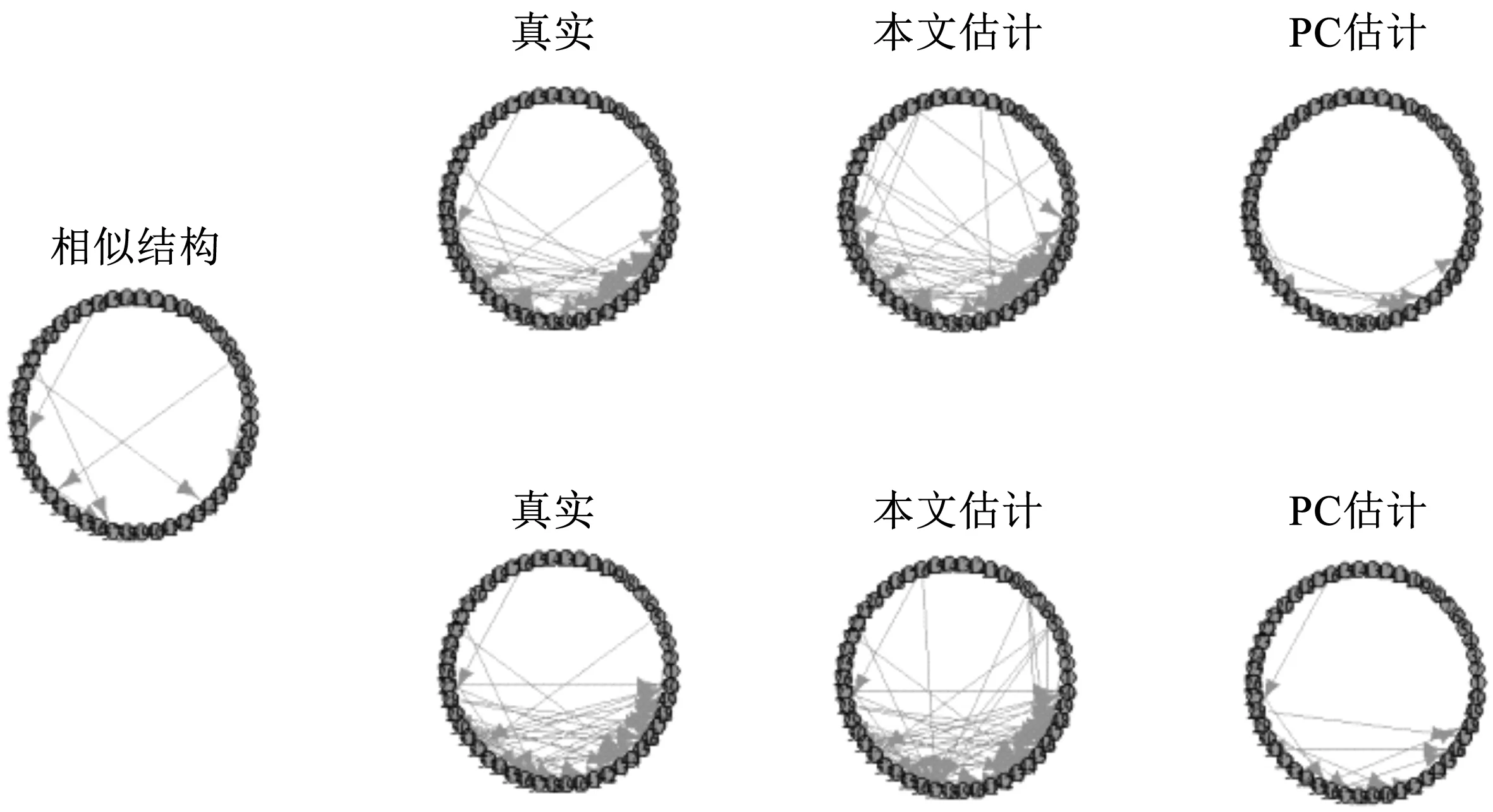
图3 实验结果

从图3可以看到,较PC算法，本文算法所估计出的有向边明显更多.另外从两种算法的恢复情况(表2)，可以看到，本文算法1的FPR较PC算法较高，这也意味着本文算法1估计出了多余的信息，但是本文算法1的FNR较低，这也说明了本文算法1能将原有向图中的信息尽可能的估计出来，从而为下一步分析奠定了基础.综上实验，可以说明本文提出的算法1能够较好地联合估计多重高斯有向图.

表2 恢复情况

5 结 论

本文主要针对多重高斯有向图进行联合估计.在具有自然偏序的条件下，当节点满足隐变量模型的时候，根据极大似然估计构建回归模型，通过坐标下降联合估计图的邻接矩阵.数值实验证明了该方法能够较高效地联合估计高斯有向图.