一类含三个圈的本原有向图的m-competition指数
宋卓蓉,高玉斌
(中北大学 理学院,山西 太原030051)
1 预备知识
本原有向图本原指数[1]的研究已经逐步扩展到了对本原有向图的scrambling指数[2-3]的研究.本原有向图的scrambling指数是一个新兴研究分支,也是近两年来在组合数学中较为活跃的一个研究方向,在计算机科学中具有广泛的实际应用背景.近年,许多学者又将scrambling指数推广到m-competition指数[4-8],进行了广泛的研究.
设D=(V,E)是一个n阶有向图,其中顶点集V=V(D),弧集E=E(D)(允许有环但无重弧).一个有向图D是本原的,当且仅当存在正整数k,使得D中的任意一点x到另外一点y(y可能等于x)都存在k长途径.称满足上述条件的最小正整数k为有向图D的本原指数,记为exp(D).
设D是一个n阶本原有向图,k∈Z+,对于任意顶点x,y∈V(D),用N+(Dk∶x)={v∈V(D)|x →kv}表示顶点x经过k长途径所到达的点的集合,用|N+(Dk∶x)|表示此集合中点的个数.用N+(Dk∶x,y)=N+(Dk∶x)∩N+(Dk∶y)表示顶点x,y经过k长途径所到达的公共点的集合,用|N+(Dk∶x,y)|表示此集合中点的个数.
如果D为一个n阶本原有向图,k为正整数,则Dk也是本原有向图,其中V(Dk)=V(D),E(Dk)={vi,vj)|在D中有vi→kvj}.
定义1[4]设D是n阶本原有向图,如果存在正整数k,对于D中任意顶点x和y,都存在m(1≤m≤n)个不同的顶点v1,v2,…,vm∈V(D)使得x →kvi,y →kvi,(1≤i≤m),满足上述条件的最小正整数k称为本原有向图D的m-competition指数,记为km(D).特殊地,k(D)=k1(D),exp(D)=kn(D).
定义2[4]设D是n阶本原有向图,如果存在正整数k,对D中两个不同的顶点x和y,都存在m(1≤m≤n)个不同的顶点v1,v2,…,vm∈V(D)使得x →kvi,y →kvi,(1≤i≤m),满足上述条件的最小正整数k称为顶点x和y的局部m-competition指数,记为km(D∶x,y).

2 主要结论及证明
设n≥7,gcd(n,3)=1,D是恰含一个n圈和两个n-3圈的n阶本原有向图.容易得出,在同构意义下,这样的本原有向图D共有三种形式D1,D2和D3(如图1~图3所示).下文将分别给出这三个本原有向图的m-competition指数.在证明过程中,顶点的指标按mod n来对待.如vn+1=v1,vn+2=v2,v0=vn,v-1=vn-1,v-2=vn-2等.

图1 有向图D 1 Fig.1 Digraph D 1

图2 有向图D 2 Fig.2 Digraph D 2

图3 有向图D 3 Fig.3 Digraph D3
定理1 设D1是如图1所示的n阶本原有向图,其中n≥7,gcg(n,3)=1,则对任意1≤m≤n,有

证明 因为gcd(n,3)=1,不妨设n=3k+1,n=3k+2(k∈Z+).
情形1 n=3k+1.
情形1.1 n+m为偶数.
观察图1中D1,顶点v2,v3,…,vn-2构成一个n-3圈,不妨将这个n-3圈记为C1.在图D1中,任取u,v∈V(D1),总存在C1中的点vi,vj(i,j=2,…,n-2),使得u →2vi,v →2vj.所以只需证明对任意i,j=2,…,n-2,均有

观察图4中Dn-31可知,v2,v3,…,vn-2点均为环点.对任意vi,vj∈V(C1)(i,j=2,…,n-2),

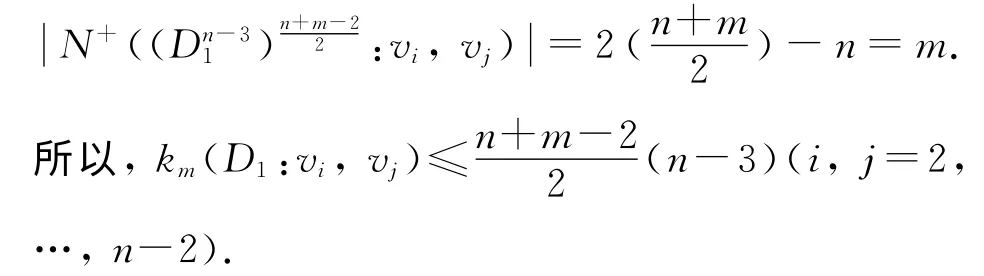

图4 有向图Dn1-3 Fig.4 Digraph Dn1-3

在图D1中,顶点v2,v3,…,vn-2构成一个n-3圈,已记为C1,任取u,v∈V(D1),总存在C1中的点vi,vj(i,j=2,…,n-2),使得u →2 vi,v →2vj.所以只需证明对任意i,j=2,…,n-2,均有
在图5的Dn1中


图5 有向图Dn1 Fig.5 Digraph Dn1
在图Dn1中,令M1为Dn1的一个导出子图.



则对任意u,v∈V(D1),均有故km(D1:由u,v的任意性,


情形2 n=3k+2.
此时本原有向图Dn-31,Dn1与情况1中的本原有向图Dn-31,Dn1的不同之处在于点的排列顺序不同,故它们是同构的,所以在这种情形下,结论亦成立.
定理得证.
定理2 设D2是如图2所示的n阶本原有向图,其中n≥7,gcd(n,3)=1,则对任意1≤m≤n,有


图6 有向图Dn-32 Fig.6 Digraph Dn-32
证明 因为gcd(n,3)=1,不妨设n=3k+1,n=3k+2(k∈Z+).
情形1 n=3k+1.
情形1.1 n+m为偶数.


1)n与m均为偶数.

2)n与m均为奇数.


图7 有向图Dn2 Fig.7 Digraph Dn2
在图D2中,顶点v1,v2,…,vn-3形成一个n-3圈,已记为C2.
在图7的Dn2图中,令M2为Dn2的一个导出子图

所 以,任 取u,v∈V(D2),均 有由u,v的任意性,可知




情形2 n=3k+2.
此时本原有向图Dn-32,Dn2与情况1中的本原有向图Dn-32,Dn2的不同之处在于点的排列顺序不同,故它们是同构的,所以在这种情形下,结论亦成立.
定理得证.
定理3 设D3是如图3所示的n阶本原有向图,其中n≥7,gcd(n,3)=1,则对任意1≤m≤n,有

[1]Brualdi R A,Ryser H J.Combinatorial Matrix Theory[M].London:Cambridge University Press,1991.
[2]Akelbek M,Kirkland S.Coefficients of ergodicity and the scrambling index[J].Linear Algebra and its Applications,2009(430):1111-1130.
[3]Huang Y,Liu B.Generalized scrambling indices of a primitive digraphs[J].Linear Algebra and its Applications,2010(433):1798-1808.
[4]Kim H K.Generalized competition index of a primitive digraph[J].Linear Algebra and its Applications,2010(433):72-79.
[5]Gao Y,Shao Y.The scrambling indices of primitive digraphs with exactly two cycles[J].Ars Combination,2013(108):505-513.
[6]Shao Y,Gao Y.The m-competition indices of symmetric primitive digraphs with loop[J].Ars Combination,2013(108):217-223.
[7]Kim H K,Pank S G.A bound of generalized competition index of a primitive digraph[J].Linear Algebra and its Applications,2012(436):86-98.
[8]Kim H K,Lee S H.Generalized competition indices of symmetric primitive digraphs[J].Discrete Applied Mathematics,2012(160):1583-1590.
——以指数、对数函数同构问题为例

