基于改进的四阶各向异性扩散的中值先验重建算法
高小帆,张 权,刘 祎,张 芳,孙未雅,桂志国,2
(1.中北大学 电子测试技术国家重点实验室,山西 太原030051;
2.中北大学 仪器科学与动态测试教育部重点实验室,山西 太原030051)
0 引 言
随着计算机断层扫描(CT)技术在医学早期预测与防治中的广泛应用,以及公众自我健康意识的提高,在不影响诊断质量的前提下,人们开始追求尽可能减少放射剂量.但由于放射剂量的降低会使重建图像噪声增大,质量退化,继而严重影响医学诊断与治疗,因此在降低辐射剂量时,重建出高质量图像的研究备受关注[1].Rust[2]等使用非线性高斯滤波器链对重建的图像进行滤波,得到了不错的降噪效果,很好地保持了边缘和细节.Lui D[3]提出了一种新颖的噪声补偿CT重建方法,提高了重建图像的信噪比.王丽艳[4]等利用待重建图像稀疏性的先验信息作为正则项,泊松噪声的负对数似然函数作为保真项来设计优化目标函数,从而达到去噪且保持细节的目的.Chen Yang[5]等通过使用非局部自适应加权先验统计方法对图像进行重建,改善了低剂量CT图像的质量.
低剂量CT投影数据噪声模型的数据特点已被广泛研究,其中Wang J[6]等人通过对多个体模反复进行实验和分析,得出低剂量CT投影数据经过对数变换后,其均值和方差呈非线性递增关系,近似服从非平稳高斯分布的结论.由于最大似然期望最大算法(MLEM)在重建过程中考虑了观测数据的统计特性,且其具有非负性、全局收敛性和计数保持的特点,能较好地改善重建图像的效果,该算法被广泛运用于对投影数据统计特性进行分析.在实际运用中,迭代次数达到一定数量后,随着迭代次数的增加重建图像的质量会出现棋盘效应,产生失真及非收敛的迭代过程.基于Bayesian理论的最大后验(Maximum A Posterior,MAP)方法,有效地解决了此问题[7],该算法考虑了低剂量CT投影数据的统计特性,通过对先验分布加入先验信息,使重建过程中进行多次迭代后仍然很好地抑制了噪声,克服了MLEM重建算法收敛慢的缺点.MAP重建的思想主要是在传统的MLEM算法基础上加入先验约束,从而达到抑制噪声、平滑图像、增强图像边缘的目的[8].但是基于传统的贝叶斯方法提供的先验信息是有限的,往往会使低剂量重建图像出现阶梯状伪影和过平滑现象[9].本文将从此问题出发对低剂量CT重建进行进一步的研究.
基于偏微分方程(Partial Differential Equation,PDE)各向异性扩散的降噪算法[10-12],可以满足图像不同强度去噪的需求,即是一种自适应的去噪技术,近年来被众多学者广泛地运用.传统的二阶偏微分降噪会出现“阶梯”效应,而四阶偏微分可以有效抑制此缺点,既可以克服“阶梯”效应,又可以根据梯度和切线方向的不同扩散程度,有效地保持边缘.本文受文献[13]的启发把该文献中提出的四阶偏微分算法用于本文,并且在此基础上与绝对差值排序检测法进行了结合,对低剂量CT图像进行降噪处理;同时在每次迭代过程中,把降噪后的重建图像引入MP重建算法的目标函数,提出一种基于改进四阶各向异性扩散的中值先验重建算法,得到了很好的重建效果.实验结果表明,本文算法既改善了图像的质量,又提高了图像的信噪比.
1 MP重建算法
Alenius等在1997年提出了MRP(Median Root Prior)重建方法.MRP法使图像的像素接近其领域的中值[14].该算法能有效地保持边缘,但不是实际意义的MAP算法,只是一个经验公式.2003年,Hsiao等在MRP的基础上,构造了辅助向量,从而提出基于中值先验(Median Prior,MP)的重建方法[15],此算法是真正意义上的MAP法.
Hsicao定义的中值先验目标函数公式为

式中:Φ(y|f)为对数型似然函数;R(f,m)为一种新型先验分布目标函数;y表示观测数据向量;f表示图像向量;m是辅助向量,与f具有相同的维数.
先验分布的目标函数如下式所示:

式中:φ为先验势函数;Nj是像素j的邻域;ωjk为权值因子,表示fj和辅助向量邻域像素mf′的相互作用的强弱,当j∈Nj时,ωjk=1,否则ωjk=0.MP使用的是绝对值势函数:R(f,m)=辅助向量邻域像素mf′选取为mj′=median{fj,w},w表示所选中值算子的窗口大小.
2 改进的重建算法
2.1 基于绝对差值排序检测的四阶偏微分方程降噪
基于偏微分方程(Partial Differential Equation,PDE)的各向异性扩散降噪法,属于自适应降噪技术,该技术是在图像的平滑区域增强平滑强度,而在边缘区域则自适应地削弱平滑强度,从而在降噪的同时避免破坏图像的边缘.由于二阶PDE降噪会出现“阶梯”效应,文献[13]中提出了一种四阶PDE降噪算法,具体的分析以及完整的公式详见文献,本文给出主要公式为


式中:fηη和fξξ分别为图像梯度方向和切线方向的二阶导数,表达式为为扩散系数函数.由扩散系数函数表达式可知:在图像的边缘处,梯度值较大,函数的值较小;在图像的平坦区域,梯度值较小,函数的值较大.由此可知,扩散系数函数利用图像梯度信息作为边缘检测算子来控制图像的平滑程度.
式(3)的离散化形式为

四阶偏微分降噪算法虽然可以克服二阶偏微分降噪出现的阶梯现象,但其去噪能力相对较弱,如果为了提升效果而增加迭代次数,又会对图像的边缘造成破坏.Roman Garnett等人在文献[16]中提出了一个局部图像统计——绝对差值排序 检 测 法(rank-ordered absolute differences,ROAD),该方法可以表示出当前像素值与其周围邻域像素值强度的差异.其具体原理在文献[16]中有详细的阐述,这里不再赘述,本文受该方法启发,用于四阶各向异性扩散的扩散函数中,其主要公式为

式中:dx,y表示像素x与y强度差的绝对值,并将d,中的值按升序进行排列,定义

式中:ri(x)表示第i小的dx,y.
ROAD提供了一个计算当前像素与它周围邻域像素之间相似度的方法.考虑到图像的内部区域和边缘的连续性,故在像素周围的八邻域中,至少有四个邻域值与当前像素的强度相似,说明ROAD值较小.而噪声会使当前像素与大多数邻域像素的强度相差较大,说明ROAD值较大.因此,通过ROAD可以用于区分边缘与噪声,故把ROAD用于四阶各向异性扩散的扩散函数中是合适的.
2.2 基于改进的四阶各向异性扩散的MP重建算法
由于MAP方法引入先验信息,从而改善了低剂量CT重建图像的质量与提高图像的信噪比,在一定程度上保持了图像的细节信息[17].基于传统的贝叶斯法只能提供有限的先验信息,故使图像过平滑且出现伪影.而改进的四阶偏微分对噪声的敏感性较高,可以根据梯度和切线方向不同的扩散程度,从而有效地保持边缘.故把改进的四阶偏微分处理和MAP算法相结合是合适的.由于基于传统的贝叶斯方法只能提供有限的局部先验信息,故把改进的四阶偏微分处理的结果运用到MP的目标函数中作为本文的正则项可以得到令人满意的效果.
本文算法的目标函数为

式中:Φ(y|f)为对数型的似然函数;U(f)为一种新的先验分布的正则模型.这里U(f)取与四阶各向异性扩散相关的先验.

式中:F(uj)为对图像进行改进的四阶偏微分处理;这里φ(Δ)=Δ2/2.
经过计算,最后的表达式为

2.3 基于改进四阶各向异性扩散的中值先验重建算法
基于改进四阶偏微分先验的MP重建算法增加了基于改进四阶偏微分的正则项,可以有效地改善重建图像的质量,但是依然会有些许块状的伪影,故本文在每次迭代中,对图像进行基于改进四阶偏微分先验的MP重建算法处理后,再对重建的图像进行改进的四阶偏微分降噪.实验结果表明,本文的算法在降噪的同时可以很好地保持图像的细节和边缘信息,提高图像的信噪比.
本文的具体重建算法如下:
1)基于改进的四阶偏微分先验的MP重建算法,见式(11).
2)在对图像进行基于四阶偏微分先验的MP重建算法处理后,对重建的图像进行四阶偏微分降噪

其中,扩散函数为

3)重复以上过程一定次数后,得到最终的重建图像.
3 实验结果与分析
3.1 重建图像比较
本文所有算法的实验仿真环境均为:计算机配置为Windows 7旗舰版32位SP1(Direct X 11)的操作系统,处理器是英特尔Celeron(赛扬)E3300@2.50 GHz双核,内存为2 GB.编程工具使用MATLAB7.6.0(R2008a).本文首先选取大小为128 mm×128 mm的Sheep-Logan头部剖面图模型作为实验对象,如图1(a)所示.本文选取大小为16 384×16 384的系统矩阵,所有实验均采用平行投影的方式,在180个角度中取128个投影方向,每个方向分配128对探测器.本文在理想投影数据中加入如下式关系的高斯噪声后对低剂量的投影数据进行仿真.

式中:i=1,2,…,N为探测器信道,N是信道总数;λi为第i个探测器获得的投影数据的平均值;σ2i为第i个探测器获得投影数据的方差;ki为第i个探测器的参数;T为系统参数;对于给定的CT采集系统,ki与T是给定的.本文参数选取为:ki=200,T=12 000.为了验证本文算法的有效性,将本文算法与传统的MLEM,MRP(Median Root Prior),对图像的每次迭代中进行MLEM重建后直接进行四阶各向异性扩散的基于四阶的算法,以及在每次重建迭代中使用基于方差的各向异性扩散降噪的算法进行了比较.
各种算法中涉及到的各种参数以及迭代次数,均为反复实验后得到的最优值,图1中的每个重建图像都是达到最优时得到的图像.由图可知,传统的MLEM重建图像的质量最差;MRP算法的结果图可以达到降噪的效果,但是有明显的块状伪影;基于四阶和基于方差重建算法对重建图像的噪声进行了一定程度的抑制且可获得比较清晰的图像,但是图像中存在比较明显的块状阴影;本文算法在消除噪声时保持了图像的边缘和细节信息,使图像达到比较优质的效果,从视觉上分析,重建效果和其他几种算法相比达到最优,初步表明本文算法是有效的.
图2为胸腔模型的实验结果.由图可知,传统的MLEM重建图像的质量最差;MRP算法的结果图可以达到降噪的效果,但是有明显的块状伪影;基于四阶和基于方差重建算法对重建图像的噪声进行了一定程度的抑制且可获得比较清晰的图像,但是图像中存在一些比较明显的块状阴影;本文算法在解决低剂量CT图像噪声问题的同时,对图像的边缘和细节信息也有较好的保持,且提高了图像的信噪比,从视觉上分析,重建效果优于其他几种算法,进一步说明该算法的有效性.
图3为骨骼组织模型图像的实验结果.所得结论与图1实验结论相同,再一次说明了该算法的有效性.
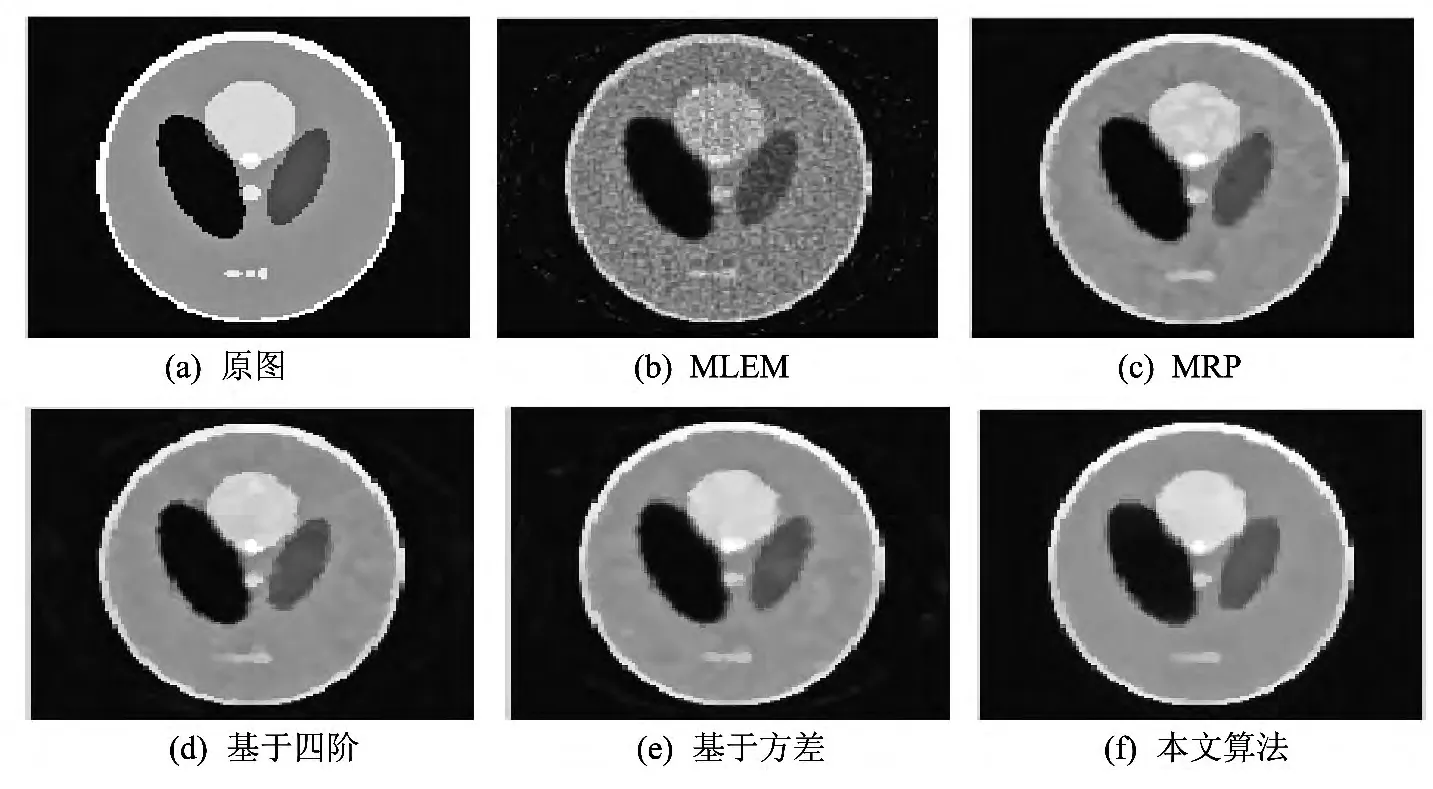
图1 Sheep-Logan头部剖面模型图像处理结果对比 Fig.1 Comparison of processing results on head profile model of Sheep-Logan

图2 胸腔模型图像处理结果对比 Fig.2 Comparison of processing results on thoracic model

图3 骨骼组织模型图像处理结果对比 Fig.3 Comparison of processing results on skeletal tissues model
3.2 重建精度比较
由上述分析可知,本文提出的算法对低剂量CT的重建图像有很好的处理能力,既可以保持图像的边缘又达到降噪的目的.本文采用以下指标对重建图像的质量进行定量的描述.
1)归一化均方误差(Root Mean Squared Error,NMSE)
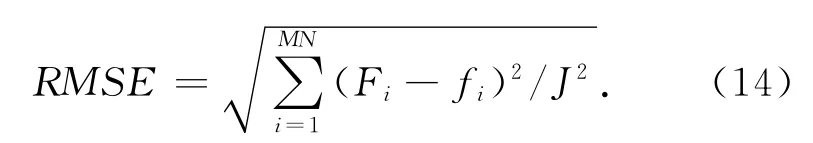
2)归一化均方距离(Normalized Mean Square Distance,NMSD)

3)均方绝对误差(Mean Absolute Error,MAE)

4)信噪比(Signal to Noise Ratio,SNR)

式中:J表示图像像素点的总和;Fi和fi分别表示重建图与原始图的第个像素的灰度值;Mi和mi分别表示重建图与原始图的均值.这些指标从不同的方面评价重建图像与原始图像的接近程度以及重建图像的质量,表1~表3为本文算法与其他算法的客观评价结果.

表1 Sheep-Logan头部剖面图模型各种算法的客观评价 Tab.1 Objective evaluation of different algorithms of the head profile model of Sheep-Logan

表2 胸腔模型各种算法的客观评价 Tab.2 Objective Evaluation of different algorithms of thoracic model

表3 骨骼组织模型各种算法的客观评价 Tab.3 Objective Evaluation of different algorithms of skeletal tissues
从表1~表3可得出本文算法的信噪比最大,且其他指标值均为最小.该结论说明本文算法的重建图像和原始图像最为接近.因此在定量评价方面,同样可以表明本算法在低剂量CT重建中是可行的.
图4,图5分别给出了本文所用的Sheep-Logan模型和胸腔模型的原始图与各种算法的重建结果图的侧面轮廓线的比较结果.从图中可以看出本文方法的重建图像与原始图像的吻合度是最高的,最接近于理想图像,具有最小的噪声波动,故本文算法可以有效地解决低剂量CT重建图像的噪声问题.

图4 头部剖面图模型各种算法第65行侧面轮廓线的对比 Fig.4 Comparison of various algorithms of the head profile model on the side of the contour line 65th

图5 胸腔模型各种算法第65行侧面轮廓线的对比 Fig.5 Comparison of various algorithms of thoracic model on the side of the contour line 65th
4 结 论
本文提出了一种基于改进的四阶各向异性扩散的中值先验重建算法.该算法先在中值先验MP算法的基础上,对目标函数进行了修订,加入改进的四阶各向异性扩散正则项,该正则项可以对重建图像进行降噪的同时保持图像的边缘和细节,从而形成基于改进四阶各向异性的MP重建算法;该算法可以很好地改善图像的质量,但是依然会存在一些块状伪影;四阶各向异性扩散对噪声的敏感性比较高,可以根据梯度和切线方向不同的扩散程度,进而有效地保持图像的边缘,结合这两种方法的优势,本文提出了基于改进的四阶各向异性扩散的中值先验重建算法,即在每次迭代中,对基于改进的四阶各向异性扩散的MP重建算法处理后的图像,再进行改进四阶各向异性扩散降噪处理,从而进一步提高图像的抗噪声性能.实验结果表明,该算法无论在主观效果还是客观效果上,均说明该算法是可行的.
[1]Linton O W,Mettler F A.National conference on dose reduction in CT with an emphasis on pediatric patients[J].American Journal of Roentgenology,2003,181(2):321-329.
[2]Rust G F,Aurich V,Reiser M.Noise dose reduction and image improvements in screening virtual colonoscopy with tube currents of 20 m As with nonlinear Gaussian filter chains[C]∥Medical Imaging 2002 Confer-ence,New York:IEEE,2002:186-197.
[3]Lui D,Cameron A,Modhafar A,et al.Low-dose computed tomography via spatially adaptive Monte-Carlo reconstruction[J].Computerized Medical Imaging and Graphics,2013,37(7-8):438-449.
[4]王丽艳,韦志辉.低剂量CT的线性Bregman迭代重建算法[J].电子与信息学报,2013,35(10):2418-2424.Wang Liyan,Wei Zhihui.Linearized bregman iterations for low-dose CT reconstruction[J].Journal of Electronics and Information,2013,35(10):2418-2424.(in Chinese)
[5]Chen Y,Gao D Z,Nie C,et al.Bayesian statistical reconstruction for low-dose X-ray computed tomography using an adaptive-weighting local nonprior[J].Computerized Medical Imaging and Graphics,2009,33(7):495-500.
[6]Li T,Li X,Wang J,et al.Nonlinear sinogram smoothing for low-dose X-ray CT[J].IEEE Transactions on Nuclear Science,2004,51(5):2505-2513.
[7]Li S T.Markov random field modeling in image analysis[M].Berlin:Springer Verlag,2001.
[8]何玲君,潘晋孝,孔慧华.自适应正则MAP的CT图像重建方法研究[J].计算机工程与应用,2011,47(28):198-200.He Lingjun,Pan Jinxiao,Kong Huihua.Adaptive regularized MAP of CT image reconstruction method[J].Computer Engineering and App Hcations,2011,47(28):198-200.(in Chinese)
[9]李晓红,张权,刘祎,等.基于小波收缩和正逆扩散结合的Pattern Recognition Letters质中值先验图像重建算法[J].计算机应用,2012,32(12):3357-3360.Li Xiaohong,Zhang Quan,Liu Yi,et al.High quality median prior image reconstruction algorithm based on wavelet shrinkage and forward-and-backward diffusion[J].Journal of Computer Applications,2012,32(12):3357-3360.(in Chinese)
[10]Cho S I,Kang S J,Kim H S,et al.Dictionary-based anisotropic diffusion for noise reduction[J].Pattern Recognition Letters,2014,46:36-45.
[11]Veerakumar T,Esakkirajan S,Vennila I.Edge preserving adaptive anisotropic diffusion filter approach for the suppression of impulse noise in images[J].AEU-International Journal of Electronics and Communications,2014,68(5):442-452.
[12]Surya Prasath V B,Vorotnikov D.Weighted and well-balanced anisotropic diffusion scheme for image denoising and restoration[J].Nonlinear Anal.Real World Appl,2014,17:33-46.
[13]Mohammad Reza Hajiaboli.An anisotropic fourth-order diffusion filter for image noise removal[J].International Journal of Computer Vision,2011,92(2):177-191.
[14]Karali E,Koutsouris D.Towards novel regularization approaches to PET image reconstruction[J].Journal of Biosciences and Medicines,2013,1(2):6-9.
[15]Hsiao I T,Rangarajan A,Gindi G.A new convex edge-preserving median prior with applications to tomography[J].IEEE Transactions on Medical Imaging,2003,22(5):580-585.
[16]Roman Garnett,Timothy Huegerich,Charles Chui.A universal noise removal algorithm with an impulse detector[J].IEEE Transactions on image processing,2005,14(11):1747-1754.
[17]Zhan Jie,Chen Wufan.Bayesian reconstruction algorithm for PET using new Markov quadratic hybrid multi-order priors[C]∥The 1st International Conference on Bioinformatics and Biomedical Engineering.New York:IEEE,2007:334-337.

