“两线法”巧析竖直面内不脱轨问题
简伟伟
(江西省横峰中学 江西 上饶 334300)
复合场中竖直平面内的圆周运动类题型,特别是该类问题中“不脱离轨道”类问题,因其知识联系性广、综合性强,是高中物理教学中的难点问题.笔者从教学实践中总结出一种分析该类问题的方法——“两线法”,该法相比“等效场法”,既能究其本质、抓住关键,又通俗易懂、方便快捷.
“两线法”就是指在以圆轨道的圆心为原点,在物体运动的圆周上沿着场力的方向作出一条参考线——“场力线”,再作出一条垂直“场力线”的参考线——“压轨线”,我们利用这两条参考线方便、清晰地突破竖直平面内不脱轨类问题的解题方法.
1 模型构建 难点突破(以仅在重力场作用下为基本模型)
【例1】如图1所示,一质量为m的小球从半径为R的固定光滑圆轨道的最低点a点,以速度v0向右运动,若它运动过程中不脱离轨道,试分析小球的运动情景.
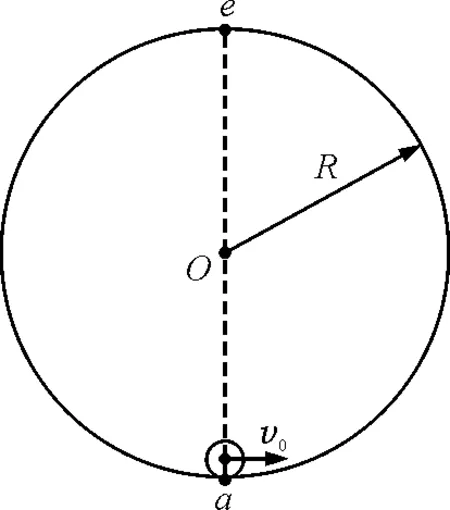
图1 例1题图
1.1 “场力线”的作用
因为只有重力场,沿着场力(此处为重力)方向作出一条参考线——“场力线”,这条线可以突破以下难点问题:
(1)圆周上什么位置速度最大?什么位置速度最小?
如图2所示,因为只有重力做功,沿着重力方向移动,重力都要做正功则其速度就要增大,可知参考面L1为沿着重力方向最低的平面,可知小球在a点速度最大,同理参考面L5为沿着重力方向最高的平面(重力做的负功最多),可知小球在e点速度最小.
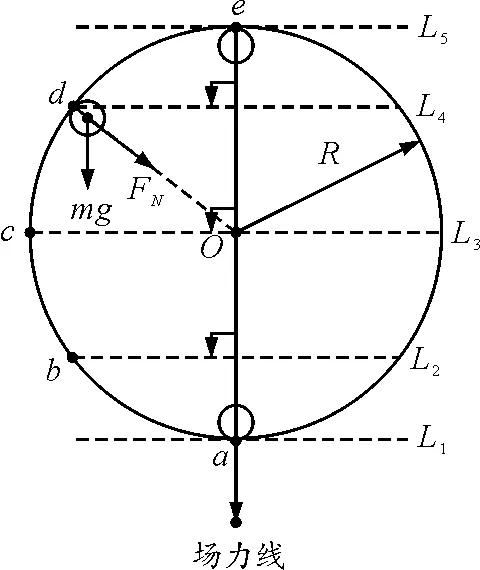
图2 速度最大和最小点分析图
总结:圆周上“场力线”最上方的位置速度最小、最下方的位置速度最大.
(2)什么位置轨道受到的压力最大?
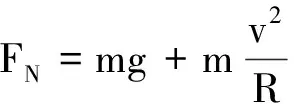
总结:圆周上“场力线”最下方的位置轨道受到的压力最大.
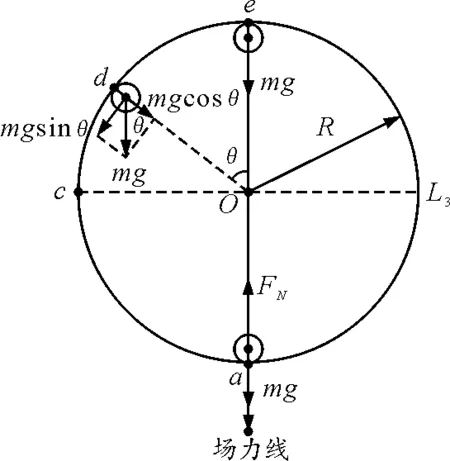
图3 轨道受压力最大和最易脱轨点分析图
(3)什么地方最易脱离轨道?
如图3所示,最小向心力为不利用轨道的弹力,仅靠重力的作用来提供向心力,由图可知在场力线上e点时,重力全部沿径向指向圆心提供向心力,可知该位置的最小向心力最大.由机械能能量守恒定律易知,在场力线的上方小球的速度会减小,即越向上运动越容易使得F提供的向心力>F需要的向心力,所以e点是小球最易脱离轨道的位置,要使得小球做完整的圆周运动,就一定要使得小球通过e点[1].
总结:圆周上“场力线”最上方的位置最易脱轨(做近心运动).
1.2 “压轨线”的作用
如图4所示,作出一条垂直“场力线”的参考线——“压轨线”,我们可知这条线将圆周一分为二,在靠近“场力线”下方的这半圆上的任何位置(如图中b点),由于重力沿径向的分力是使小球有紧压轨道的效果.在靠近“场力线”的上方的这半圆上的任何位置(如图中d点),由于重力沿径向的分力具有使小球脱离轨道的效果.因此,这条线是场力是否紧压轨道的分界线,笔者把它简称为“压轨线”.利用这条线可以突破以下难点问题.
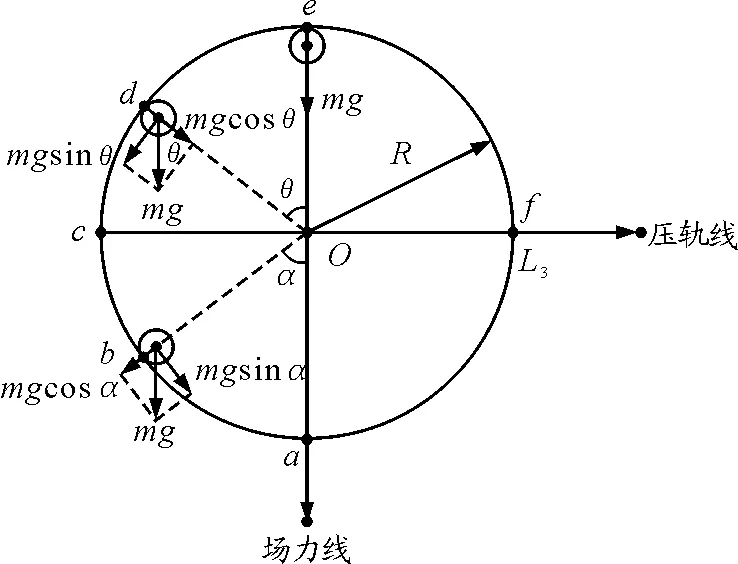
图4 不脱轨范围和不脱轨条件分析图
(1)小球在什么范围内运动一定不会脱轨?
通过上面的分析我们可知,在“压轨线”靠近“场力线”下方的半圆上的任何位置,即使小球速度为零,小球还是会紧贴轨道.在靠近“场力线”上方的这半圆上的任何位置,由于重力沿径向的分力是使小球脱离轨道的效果,当小球速度小于某一值(由所需的向心力决定),小球会脱离轨道而做近心运动.
总结:“压轨线”是我们分析小球速度为零时,小球是否会脱离轨道的参考线.
(2)小球在圆周上运动时不脱离轨道要满足什么条件?
综上分析可得:小球要不脱离轨道,要么通过“场力线”的最上方的位置做完整的圆周运动,要么在“压轨线”靠近“场力线”下方的半圆上来回运动.
2 实战演练 体验功效(以重力场和电场相交汇的复合场为普遍范例)
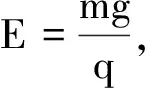
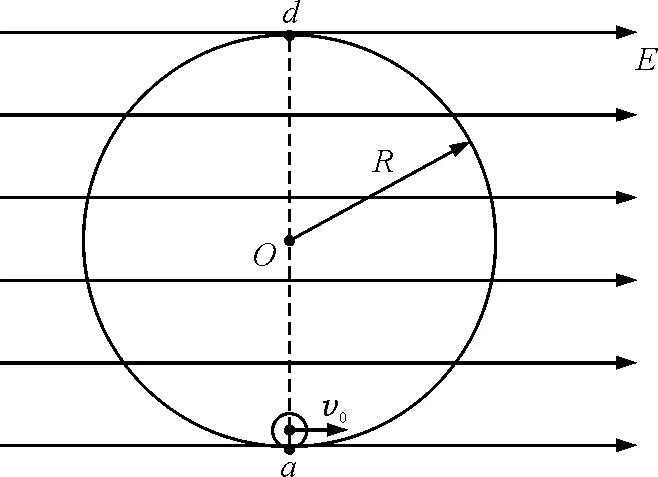
图5 例2题图
分析:(1)受力分析,作出两线
如图6所示,分析小球所受到的场力(重力、电场力),作出场力的合力,则该合力的方向即为“场力线”的方向,作“场力线”的垂线,即为“压轨线”.

图6 “场力线”和“压轨线”示意图
(2)巧借两线,突破难点
如图7所示,我们过圆轨道的圆心,作出“场力线”和“压轨线”.
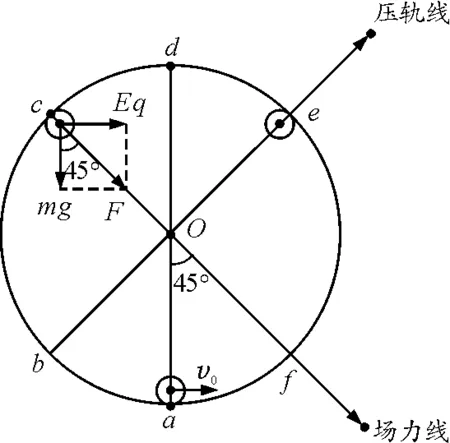
图7 “场力线”和“压轨线”解题图
利用“两线法”原理我们知道,要使小球不脱离轨道,有两种情况:1)在“压轨线”下部分半圆(bfe)上来回运动,临界情况为到b点或e点速度恰好为零;2)恰好以最小的速度过c点,在圆周上做完整的圆周运动.
(3)结合分析,列式求解
解:要使小球不脱离轨道有以下两种情况.
1)在半圆(bfe)上来回运动,设其以初速度v运动,当其到达e点速度恰好为零,由动能定理得
解得
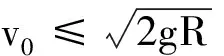
2)小球在圆周上做完整的圆周运动,而不脱离轨道.设以初速度v′运动,当其恰好通过c点时,有
-EqRsin 45°-mgR(1+cos45°)=
解得
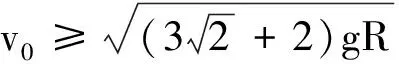
综上所述,要使小球在圆轨道上运动过程中不脱离轨道需满足
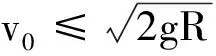
由以上对重力场和电场的普遍范例分析可以看出,利用“两线法”处理竖直平面内不脱轨类问题时,内在上可以从本质上分析各个临界点的形成因素,外在上又能以简单直观的方式告诉我们如何寻找这些临界点,可谓既究其本质,又通俗易懂.

