Maple动画在力学教学中的应用*
孟 勇
(宁波大学物理科学与技术学院 浙江 宁波 315211)
1 引言
物理学是一门研究物质最一般的运动规律和物质的基本结构,以及物质之间相互作用的基础性学科, 在众多的自然学科中一直属于基础学科,同时又发挥着带头学科的作用.这也使得大学物理作为一门让理工科大学生初步熟悉自然界物质运动、结构、相互作用规律, 为后续的专业课程学习及进一步获取有关知识奠定必要物理基础的课程显得尤为重要. 但是,由于大学物理中绝大多数名词概念、物理量的定义,以及问题的求解计算都紧密结合着微积分、线性代数等数学知识与技巧,而且在传统教学过程中教师只能进行口头传授和板书阐述,缺少对实际物理过程的形象化、可视化的演示,使得大学生在学习大学物理这门课程时可能会感觉抽象、难懂、不直观、不易学.
大学物理之所以难学,究其原因除了对学生数学与逻辑思维能力要求高之外,就是缺少作为灵魂的“核心素材”,真正意义上的反应真实世界的物理图形和物理动画.Maple是当今世界四大主流的数学软件之一[1,2],不仅具有非常强大的数学符号计算功能和简单易学的编程功能,而且通过它丰富的程序包可以绘制各种高精准的图形与科技动画,这是一般的像C语言、Fortran语言以及Flash动画制作软件所无法比拟的.所以,应用Maple软件制作动画在大学物理多媒体课程教学中显得大有裨益.可以实现一种让学生更为直观地了解物理模型、弄清物理过程的可视化教学[3~6].本文以力学教学中3个经典问题为例,通过计算,然后制作相应的动画来说明Maple动画在力学教学中对激发学生学习兴趣,提高逻辑思维能力,认清物理本质的作用.
2 经典问题
2.1 傅科摆
傅科摆如图1所示,是法国物理学家傅科为了证明地球是在自转, 于1851年做了一次成功的摆球实验.在傅科摆实验中,人们观察到随着摆球的摆动,摆平面沿着顺时针方向缓慢转动,转动方向不断变化.由惯性定律可知, 摆在摆动平面方向上不受外力作用, 摆动的空间方向应该不会变化, 而之所以观察到摆动平面在不断变化是因为在相对运动中,观察者所在的参考系(地球)正在沿着逆时针方向转动, 才产生这种奇异的现象, 从而有力地证明了地球在自转.

图1 法国巴黎的傅科摆
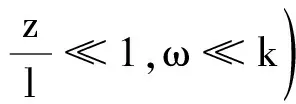
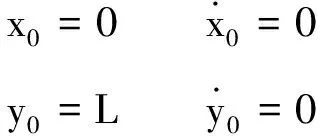
(1)
时运动学方程为
x=Lsin(αt)cos(kt)
(2)
y=Lcos(αt)cos(kt)
(3)
z=const
(4)
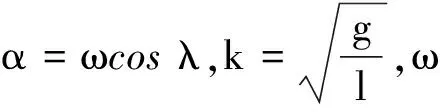
restart:with(plots):with(plottools):#导入图形软件包
eq1:=x=Lsin(αt)cos(kt); #摆球的x方向坐标
eq2:=y=Lcos(αt)cos(kt); #摆球的y方向坐标
L:=30;k:=0.3824508553;α:=0.000 049 497 701 32; #设定相关的参数
eq3:=subs(t=300·i,rhs(eq1)); #将摆球的x轴方向的运动加速300倍
eq4:=subs(t=300·i,rhs(eq2)); #将摆球的y轴方向的运动加速300倍
eq5:=subs(i=j,eq3); #为画出轨迹线进行变量替换
eq6:=subs(i=j,eq4); #为画出轨迹线进行变量替换
noffm:=300;#设定动画时长
forifrom0by1tonoffmdo#开始图像编程
ms1:=sphere([eq3,eq4,5],3,color=red); #画出每一帧的摆球
ms2:=sphere([0,0,64.908 263 0],1,color=pink);#画出傅科摆的悬挂点
rod[i]:=curve([[0,0,64.9082630],[eq3,eq4,5]]);#画出每一帧的摆绳
Q1:=curve([seq([subs(i=j,eq3),subs(i=j,eq4),0],j=0..i)],
color=COLOR(RGB,0.5450980392,0.321 568 627 5,0.176 470 588 2),linestyle=3,thickness=1);#画出摆球在O-x-y平面的运动轨迹
anima[i]:=display({rod[i],ms1,ms2,Q1}); #将每一帧所有图形组合放在同一幅图上
enddo:#完成图像编程
display([seq(anima[i],i=0..noffm)],title=
’加速300倍的傅科摆’,titlefont=[TIMES,
ROMAN,20],insequence=true,scaling=constrained) #将每一帧图像连接在一起依次播放形成动画
动画效果如图2所示.
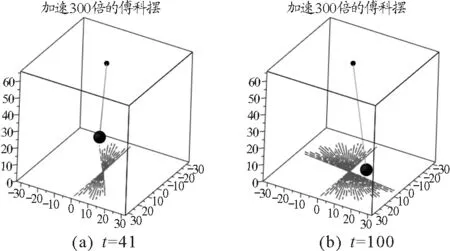
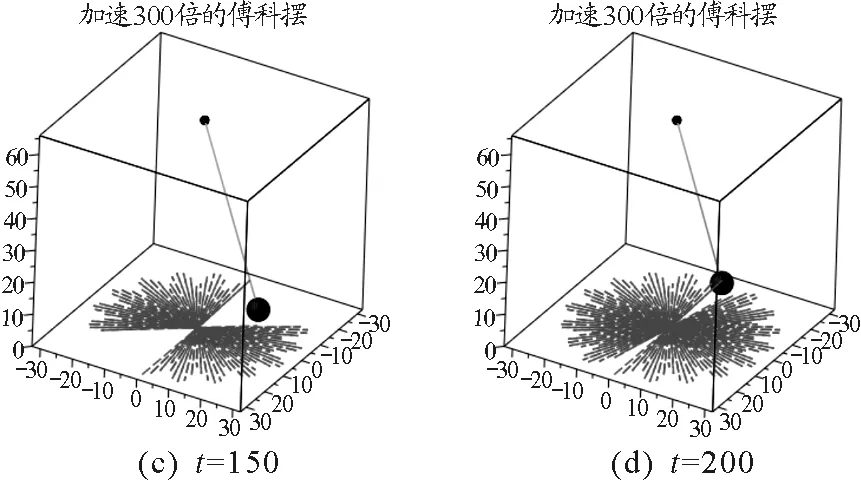
图2 不同时刻的傅科摆
通过Maple制作的傅科摆动画能清楚明了地观察到在摆球运动过程中,摆平面在不断地发生变化,以及摆球运动轨迹.从而以动画的形式说明了地球在自传,也加深了学生对科里奥利力的理解.
2.2 波的干涉
波的干涉是指具有相同振动方向、频率一致以及稳定的相位差的两列或者多列波(相干波)在空间中相遇,使得某些区域里振动加强,而在另外一些区域里振动减弱,振动加强与减弱区域相隔开,这种现象就叫波的干涉.
设两个频率相同的波源,其振动方程分别为
y10=A10cos(ωt+φ1)
(5)
y20=A20cos(ωt+φ2)
(6)
从而形成的两列波的波动方程分别为
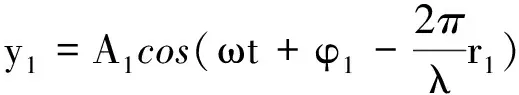
(7)
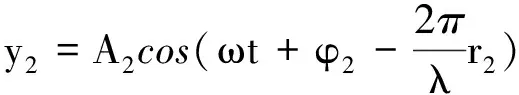
(8)
根据波的叠加原理,可以算出两列波在空间p点处叠加之后合振动方程为
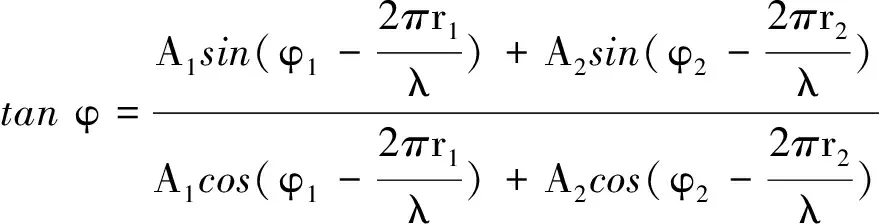
(9)
restart:with(plots):with(plottools):#导入图形软件包
forifromby1to100do;#进行振源图像的编程
ms1:=sphere([-1,0,cos(i)],i,color=red);#制作每一帧红色振源小球
ms2:=sphere([1,0,cos(i)],i,color=blue);#制作每一帧蓝色振源小球
anima[i]:=display({ms1,ms2});#将两个振源小球放在一幅图像中
enddo:#完成振源图像的编程
Q1:=display([seq([anima[i],i=0..100]),title=
′′波的干涉′′,titlefont=[TIMES,ROMAN,20],
insequence=true,scaling=constrained,axes=box):#将每一帧振源振动图像连在一起依次播放形成动画
食品微生物检测的内容。首先是致病菌。一旦食品中含有较高含量的致病菌,就容易导致人体中毒,因此需要重点检测食品中的致病菌。其中,蜡样芽孢杆菌与金黄色葡萄菌是食品中的主要致病菌,在微生物检测实践中,需要科学检测这些致病菌的数量。其次是指示性菌种。一般情况下,从两个方面来检测指示性菌种。一是科学检测菌落总量,以便合理判断食品污染程度。在检测实验中,通常会取出1g食品,然后检验其菌落数量。二是合理检测大肠杆菌群。研究发现,人、牲畜的粪便是菌种的主要来源,因此就需要将大肠杆菌群作为污染指标菌,以此来评价食品卫生达标状况。
Δφ:=phi2-phi1-2·Pi·(r2-r1)/λ ; #计算振幅相位差
A:=sqrt(A12+A22+2·A1·A2·cos(Δφ));#计算合振幅
r1:=sqrt((x-x1)2+(y-y1)2); #计算振动点与红色振源距离
r2:=sqrt((x-x2)2+(y-y2)2); #计算振动点与蓝色振源距离
M:=phi1-2·Pi·r1/λ;#为了书写方便设置变量
N:=phi2-2·Pi·r2/λ;#为了书写方便设置变量
phi:=arctan( (A1·sin(M)+A2·sin(N))/ (A1·cos(M)+A2·cos(N)));#计算合振动的初相位
A1:=1;A2:=1;phi1:=0,phi2:=0;x1:=-1;y1:=cos(t);x2:=1;y2:=cos(t);λ:=0;ω:=1; #设定相关参数
eq0:=A·cos(ω·t+phi); #写出合振动的表达式
Q2:=animate(plot3d,[eq0,x=-10..10,y=-10..10],t=0..100,frames=100):#制作合振动的动画
display([Q1,Q2]) #将振源动画与合振动动画叠加在一起,完成干涉动画的制作
动画效果如图3所示.
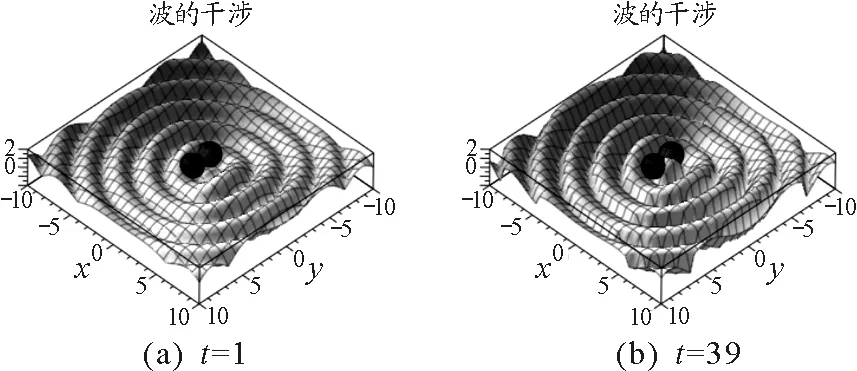
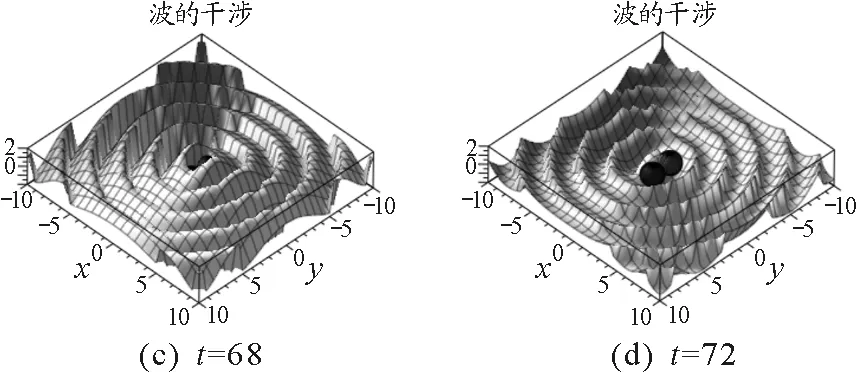
图3 不同时刻波的干涉
从干涉动画中可以看出有些区域干涉相长使得振动始终加强,有些区域干涉相消导致振动始终减弱,实现了能量在空间上的重新分布.
2.3 地球同步卫星的变轨运动
日月星辰交相辉映,自古以来就吸引着人们探究天体运行的规律.而天体运动的常见问题就是开普勒问题,它是指质点在势能与距离成反比的外场中如何运动的问题,该问题的解决一直是力学教学中的重点内容.
由于万有引力是保守力,系统能量守恒.在极坐标系下可以用公式表示为
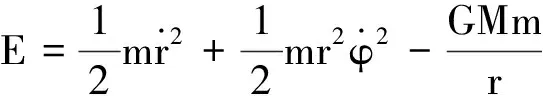
(10)
又因为万有引力是有心力,系统角动量守恒
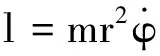
(11)
由式(10)和式(11)可以得到天体运动的圆锥曲线公式为
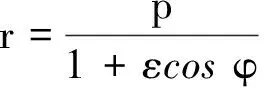
(12)
其中焦参数
离心率
由于离心率的不同其圆锥曲线有着不同的形状与类型,而从上面的离心率公式可以看出,通过改变能量的大小就可以改变其运行轨道类型.即
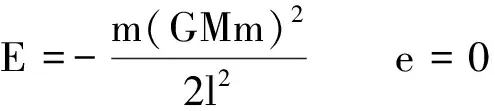
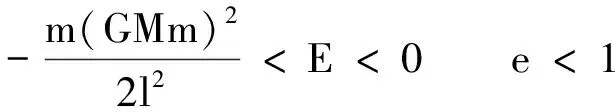
E=0 e=1 抛物线
E>0 e>1 双曲线
但是,仅凭若干抽象的公式可能无法在学生脑海中留下深刻印象,于是本文以地球同步卫星为例,制作因速度的大小导致其轨道类型发生改变的动画,这样通过数与图像动画相结合的方式,加深学生对于开普勒问题的理解与掌握.
制作的动画如图4所示.(由于制作程序代码过长,故不在此给出)
从图4可以清楚地看到地球同步卫星因初始速度的不同而产生各种变轨运动,同时还在动画中加入了计时功能,使得动画以一种高精确性与观赏性的特征展现给学生看.
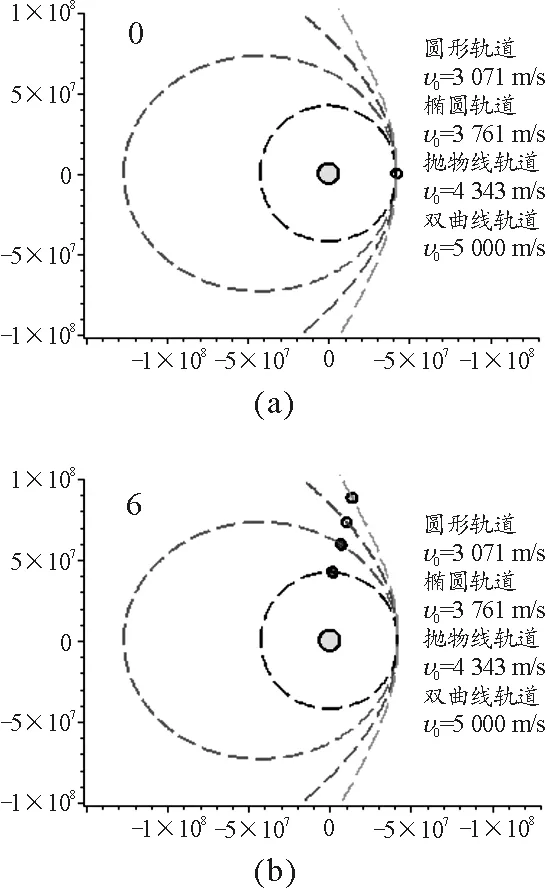
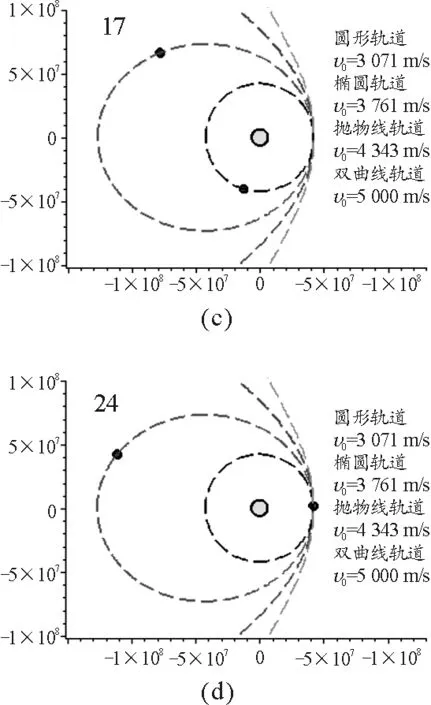
图4 地球同步卫星的变轨运动
3 结束语
Maple动画不仅实现了多媒体生动形象性与科学逼真性的完美融合,同时也弥补了实验教学的不足. 大学物理教师通过Maple动画来进行可视化教学,可以将复杂、抽象、难懂或者用言语表达十分困难的物理问题或者物理过程以生动形象的动画直观展示给学生看,让学生了解物理过程,掌握整个物理图景.比起课本上几张静态的图片, 使用动画更能在学生脑海中留下深刻的印象, 引起学生关注, 增加学生的学习积极性,也因此提高了教学质量.

