一类非对称均匀分布参数的耐抗性的估计及其优良性

郑成秋，王 迪，祁 鹤，徐 宝

均匀分布是一种常用的连续型分布，在理论上，它为证明随机变量存在定理做出重大贡献，在贝叶斯统计中，它还被用于某些参数的先验分布［1］，而且任何随机变量经由它的分布函数形成的随机变量的分布都是均匀分布族中的特殊一员U(0, 1)［2］，从而它与任何分布都能建立起联系.应用上，它广泛存在于流行病学，遗传学，交通流理论等许多概率模型中.因此关于均匀分布相关的统计推断成为许多学者一直研究的内容.Rossman A.I.，Short T.H.，Parks M.T.在 1998 研究了均匀分布参数的贝叶斯估计［3］；许多学者研究了均匀分布参数的矩估计、极大似然估计及其性质［4-8］，讨论了一类特殊均匀分布参数的抗耐性估计和分布区间中心的点估计量［9-10］.均匀分布有着各种不同的类型，即不同的定义区间，本文在上述研究的基础上，研究一类非对称均匀分布参数的估计及其性质.耐抗性是提供对于数据的局部不良行为的非敏感性［11-12］，故本文在已有文献的基础上，利用样本的四分位矩这样具有耐抗性质的统计量，得到了一类非对称均匀分布U(θ, 0)的参数θ的估计量θˆn，并讨论了它的优良性.

1 预备知识

定义1［1］若随机变量X的密度函数为θ，则称该分布为区间(, 0)上的均匀分布，记作X～U(θ, 0).其分布函数为

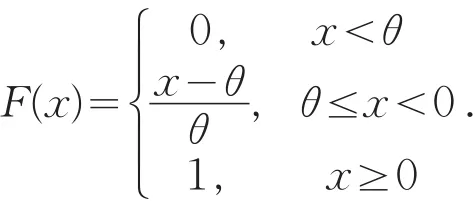
定义2［1］设X1,X2,…,Xn为抽自某个已知总体的一组简单随机样本，X(1),X(2),…,X(n)为相应样本的次序统计量，称为样本X1,X2,…,Xn的中位数.

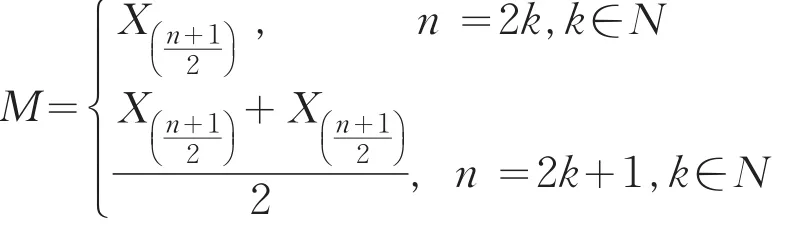
在上述定义的基础上，我们给出如下样本深度、四分位矩等概念.

定义3设X1,X2,…,Xn为抽自某个已知总体的一组简单随机样本，X(1),X(2),…,X(n)为相应样本的次序统计量，称为样本的 深 度.称样 本X1,X2,…,Xn四分位数的深度，其中表达式[x]表示取整函数，即不大于x的最大整数.

定义4设X1,X2,…,Xn为抽自某个已知总体的一组简单随机样本，X(1),X(2),…,X(n)为相应样本的次序统计量，称为X1,X2,…,Xn的下四分位数，称FU=为样本X1,X2,…,Xn的上四分位数，称dF=FU-FL为样本X1,X2,…,Xn的四分位矩.

无偏性是估计量应满足的一个基本要求，无偏估计以及渐进无偏估计的定义如下.

定义5［1］设X1,X2,…,Xn为抽自某个已知总体的一组简单随机样本，统计量是该总体参数θ的一个估计量，若∀θ∈ Θ ，有，则称为θ的一个无偏估计，否则称θˆn为θ的有偏估计.若当样本量n→ ∞ 时，则称为θ的渐进无偏估计.

2 均匀分布U(θ, 0) 的四分位矩估计及其性质

下述定理基于样本X1,X2,…,Xn的四分位矩dF给出了参数θ的估计量.

定理1设X1,X2,…,Xn为抽自均匀分布X～U(θ, 0) (θ＜0) 的一组 简单随机样本 ，X(1),X(2),…,X(n)为相应的次序统计量，dF为由次序统计量生成的样本的四分位矩，若用样本的四分位矩作为总体四分位矩的估计，则可以得到参数θ的一个估计量θˆn=-2dF.

证明 首先，计算均匀总体U(θ, 0) (θ＜0)的四分位矩.根据四分位矩的定义，由解得，同理由解得

其次，计算样本X1,X2,…,Xn的四分位矩，将分别在n=4m，n=4m+1，n=4m+2，n=4m+3四种情况下加以讨论.

当n=4m时，中位数的深度相应的四分位数的深度为k=，上四分位数和下四分位数分别为和因此，四分位矩为dF=FU-FL=

若用样本的四分位矩作为总体的四分位矩的估计，则可以得到参数θ的如下形式的估计量

同理可得，当n=4m+1时，参数θ的估计量为时，参数θ的估计量为θˆn=-2dF=2[X(m+1)-X(n-m)].当n=4m+3时，参数θ的估计量为

由四分位矩这样具有耐抗性质的统计量得出的参数的估计量，同样具有很好的耐抗性质，能够体现出对于数据的局部不良行为的非敏感性.下述定理证明了均匀分布X～U(θ, 0) (θ＜0)的参数θ的四分位矩估计量θˆn=-2dF还是θ的渐进无偏估计.

定理2设X1,X2,…,Xn为抽自均匀分布X～U(θ, 0) (θ＜0)的一组简单随机样本，X(1)，X(2),…,X(n)为相应的次序统计量，dF为由次序统计量生成的样本的四分位矩，参数θ的一个估计量是渐进无偏估计.

证明 估计量θˆn是参数θ的渐近无偏估计，即

由于

从而当n=4m时，有当

同理可证，当n=4m+1时，有时，有

综上所述，当n=4m，n=4m+1，n=4m+2及n=4m+3时，均有，因此估计量θˆn是参数θ的渐近无偏估计.一个好的估计量应该等于被估计参数，即一个随机变量，它所取的值应集中在未知参数的真值或均值附近.由四分位矩得出的估计量是参数的渐近无偏估计，即当样本容量n无限增大时，近似无偏的估计量.

3 结论

均匀分布是一种常见的连续型分布，由于其定义区间有诸多不同的形式，因此关于区间端点参数的估计形式也有很多，本文关注定义区间在坐标原点左侧的均匀分布U(θ, 0) (θ＜0)左端点参数q的估计问题，基于四分位数得到了端点参数的四分位估计，并且还证明了这一估计具有渐进无偏估计，在一定程度上丰富了均匀分布参数估计的形式与内容，并能对均匀分布族进一步的理论和应用研究方面起到一定的参考作用.