基于二头猫态和真空态下腔光力系统中的线性熵和保真度

彭基柱，许业军，臧学平

池州学院机电工程学院量子信息与光电信息交叉研究中心,安徽池州，247000

近年来，腔光力学成为一个快速发展的研究领域，并与其他学科结合形成了交叉学科[1]。腔光力系统在量子信息处理方面具有很重要的潜在应用价值[2-3]。作为量子信息应用技术重要资源的量子纠缠，在量子信息处理中具有十分重要的作用。基于腔光力系统制备纠缠态的理论和实验研究取得了丰富的成果。纠缠度是指量子态具有多少纠缠量，量子信息研究中测量这一重要的参量十分必要，以便有效提高制备量子态的纠缠程度[4]。同样，量子态的保真度也是量子信息科学的重要物理量，它关系到传递信息的准确性和可靠性，即必须考虑信息的失真问题[5]。在量子光学的研究中，通过对两种宏观完全可辨的相干态进行线性叠加获得的薛定谔猫态称为二头猫态，由于其具有独特的非经典性，被广泛应用于如量子高精度探测、量子信息处理等量子科学研究中[6]。因此，考虑光场初态为二头猫态的腔光力系统，研究其光场与振子相互作用过程的量子态特性，有助于深入了解腔光力系统的物理机理。基于上述原因，选取二头猫态作为腔光力系统光场输入态，采用线性熵的方法研究系统的纠缠特性，并数值计算系统的保真度，通过分析系统初始参数对光场线性熵和系统量子态保真度的影响，探讨两者之间的关联性。

1 系统的动力学演化

考虑一个由腔长为L的光学谐振腔和有效质量为M的机械振子构成的腔光力系统，其哈密顿量描述为[7]:

H=ћωoa+a+ћωmb+b-ћga+a(b++b)

(1)

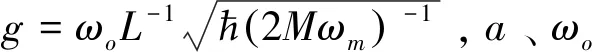
U(t)=e-irta+aeik2(a+a)2(t-sint)eka+a(ηb+-η*b)e-itb+b

(2)

这里，η=1-e-it，标度时间t=ωmt′(实际时间为t′)，标度耦合强度k=g/ωm,r=ω0/ωm。在相互作用绘景中，相应的演化算符为:

UI(t)=eik2(a+a)2(t-sint)eka+a(ηb+-η*b)

(3)

|ψ(t)〉=UI(t)|ψ(0)〉

(4)

其中，|φn(t)〉m=|kn(1-e-it)〉m。迹去系统密度矩阵ρ=〈ψ(t)|ψ(t)〉的机械模部分，可得光场约化密度矩阵:

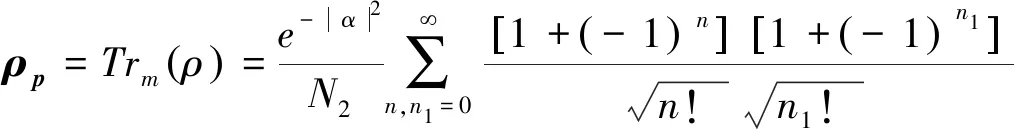
(5)

2 系统保真度和光场线性熵

2.1 保真度和线性熵的计算

腔光力系统演化过程中量子态与初态之间的保真度定义为[9]:

Fs=Tr(ρρ0)=|〈ψ(0)|ψ(t)〉|2

(6)

(7)

(8)

光场线性熵反映子系统光场与机械振子之间的纠缠程度，纠缠度高有利于量子信息的远程传输。

2.2 光场参量的影响

当系统标度耦合强度k=0.5时，系统量子态保真度Fs和光场线性熵Sp随时间的演化见图1。由图1可知，Fs和Sp作周期性的振荡，周期都为2π；Fs与Sp处于反相态：当t=2nπ时，Fs=1，Sp=0，系统恢复到初态，光场与机械振子之间为非纠缠；当t=(2n+1)π时，Fs处于极小值，而Sp处于极大值。

图1 系统保真度和光场线性熵的演化(k=0.5)

当耦合强度k=0.5，t=(2n+1)π时，系统量子态保真度Fs和光场线性熵Sp随光场参量α的变化见图2。结合图1、图2可以看出，随着α取值增大，Fs的极小值单调递减至零，即量子态传输时完全失真；Sp的极大值则单调递增。

图2 系统保真度极小值和光场线性熵极大值(k=0.5)

2.3 耦合强度的影响

当参量α=1.25，耦合强度k分别取0.5、1和1.5时，系统量子态保真度Fs和光场线性熵Sp随时间的演化见图3。由图3可知，当k=m/2(m=1，2，3…)时，Fs和Sp具有周期振荡特性，周期为2π。随着k(或m)取值的增大，Fs(Sp)处于极小值(极大值)的时间变长，Fs和Sp在t=2nπ附近变化速率增大。

当参量α=1.25，耦合强度k分别取0.125、0.25和0.75时，系统量子态保真度Fs和光场线性熵Sp随时间的演化见图4。结合图3、图4可知，当k≠m/2，Fs演化的周期不再等于2π，原因是当k2n2等于整数时，(8)式中[1+(-1)n]2eik2n2(t-sint)项周期为2π；而随着k的增大，Sp演化的周期保持不变，在t=2nπ附近增大速率增大。

图3 系统保真度和光场线性熵的演化(α=1.25,k=m/2)

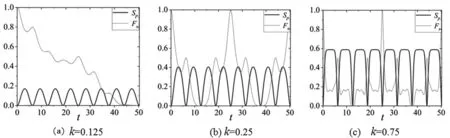
图4 系统保真度和光场线性熵的演化(α=1.25,k≠m/2)

当t=(2n+1)π时，光场线性熵Sp随耦合强度k的变化和随光场参量α的变化见图5。结合图3、图4和图5可看出，当α>1时，Sp极大值在k∈[0,0.5]时为逐渐增大到某一稳定值；而Sp极大值在k∈[0.5,2]时则是维持在稳定值。

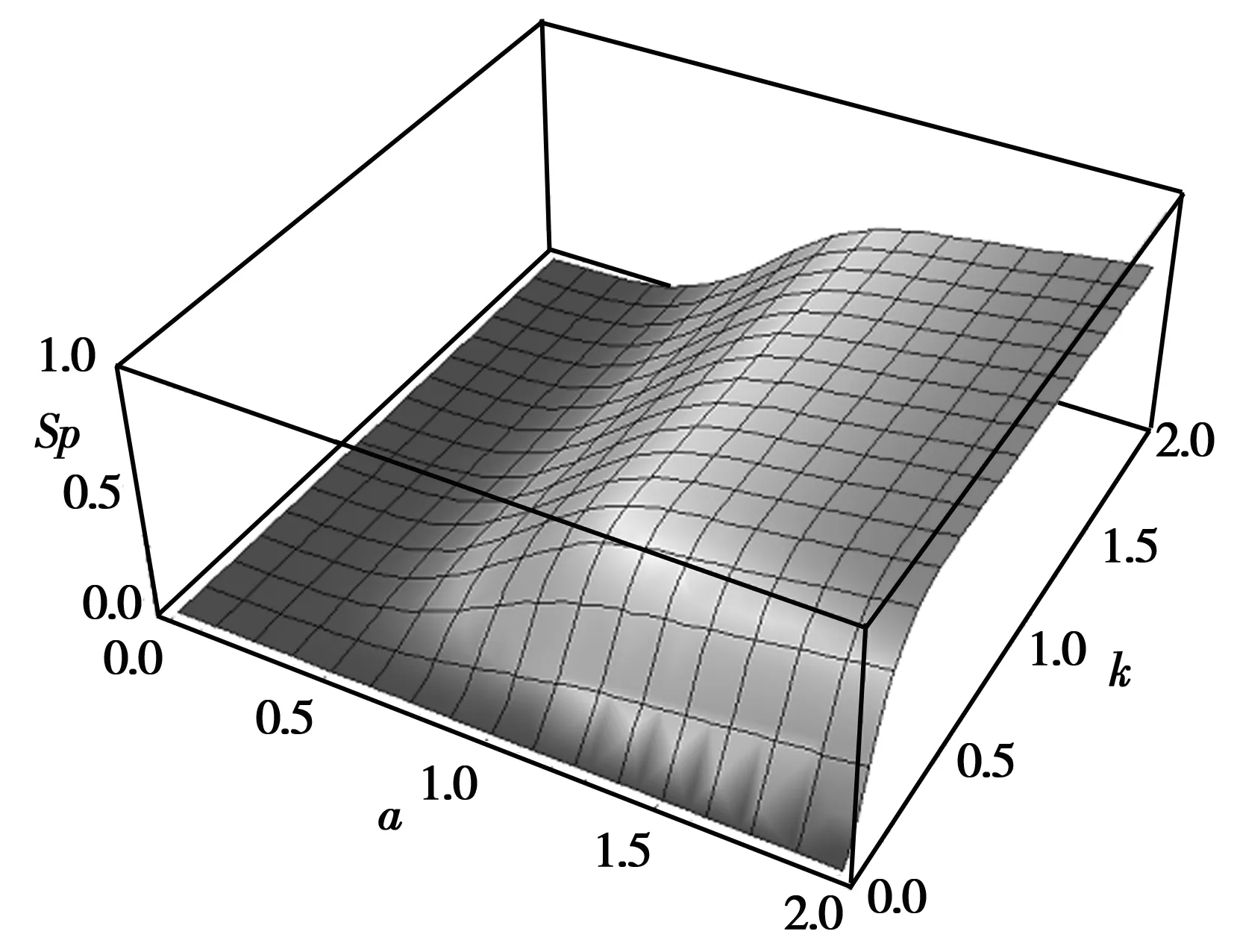
图5 光场线性熵极大值

3 结 论

研究了基于二头猫态和真空态下腔光力系统中的光场线性熵和系统量子态保真度，讨论了光场参量初态α、耦合强度k对光场线性熵和系统保真度的影响。结果发现：当k=0.5时，光场线性熵和系统保真度具有周期性振荡和处于反相态，两者存在一定程度的关联；增大α值分别使光场线性熵极大值增大和系统保真度极小值减小；光场线性熵周期不随k变化，而系统保真度周期则受k的影响，但当k为0.5的整数倍时，两者周期总是2π。以上结果在量子信息处理中有潜在应用价值。