多体量子态全可分的一个纠缠判据
王银珠,黄 丽
(太原科技大学 应用科学学院,山西 太原030024)
0 引 言
是H 上 的 纯 态.设H =H1⊗H2⊗… ⊗Hm,dimH≤+∞,|ψ〉∈H 称为全可分的,如果
众所周知,量子纠缠态是一种很重要的物理资源[1].目前对于纠缠态的识别问题已有很多著名的结果[2-7],但是仍无法有效地鉴别所有的量子态.记S(H)表示空间H 上的全体量子态组成的集合.设ρ∈S(H),如果ρ2=ρ,则ρ为纯态,否则称ρ为混合态.一般地,纯态用Hilbert空间中的复单位向量表示,记为|ψ〉,ρ=|ψ〉〈ψ|是其对应的密度算子.而混合态一般可表示为纯态的凸组合形式,即ρ=∑ipiρi,这里pi≥0,∑ipi=1,ρi

首先给出一些符号.设H1,H2分别是与量子系统1,2相结合的可分复Hilbert空间,dimHi=di(i=1,2,),M 是量子系统H1⊗H2上的可观测量算子.设ρ是H1⊗H2上的量子态,记〈M〉ρ=Tr(ρM)表示可观测量M 在量子态ρ 上的平均值,δ2ρ〈M〉=〈M2〉p-〈M〉2p表示可观测量M 在量子态ρ 上的 方 差.设{M(i)k }d2ik=1分别为d2i个作用在Hi
上的不可交换的可观测量,它们组成了可观测量空 间 的 一 组 正 交 归 一 基, 可 以 证 明Tr(M(i)kM(i)i)=δkl,这里δ是特征函数,Tr(·)是迹运算,且这里另 外 注 意 到当且仅当ρi 是M(i)
k 的本征态.许多
观测量(LOOs).2003年,Hofmann H F 引入局域不确定关系(Local uncertainty relations),提出了一个两体量子态的纠缠判据[8].文献[8]给出了如下的局域不确定关系,描述为:设{M(i)k}d2ik=1分
别为d2i个作用在Hi上的不可交换的可观测量,则一定存在ui>0,使得
对每一个i=1,2成立.进一步根据文献[9],这里的ui可取为di-1,故进一步,文献[8]提出了一个两体量子态的纠缠判据,其描 述 为:令且如果ρ∈S(H)可分,则,其中一般地,当M(i)k形式较复杂时给出这样的ui比较困难. 对 于 单 量 子 比 特 情 形, 可 取作为系统的一组局域正交可观测量,这里σx,σy,σz为Pauli矩阵,I2为二阶单位矩阵,注意到

2009年,Ma Zhihao等基于局域正交可观测量所定义的斜信息提出了与局域测不准关系判据对偶的纠缠判据[10],描述为:设
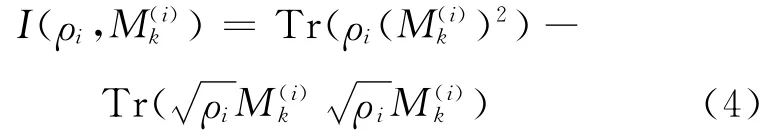
众所周知,识别多体量子态的纠缠性越来越引起国内外学者的关注,最近利用局域正交可观测量以及斜信息探测量子态的纠缠性问题也取得了一些值得关注的结果,2014 年,Yu[12]和Saboia[13]分别利用斜信息以及不确定关系研究了量子态的关联性.2015年,作者Guo[14]使用不确定关系研究了XY 自旋链的关联性.本文主要利用多体复合系统的局域正交可观测量得到了多体量子态全可分的若干必要条件,推广了文献[9-10]的有限维两体量子系统的相应结果.
为了给出本文的主要结果,作如下定义:如果1≤k≤d2i,{M(i)k}d2ik=1分别为d2i个作用在Hi上的不可交换的可观测量(i=1,2,…,m),如果d2i<k≤n,n=max{d2i,i=1,2,…,m},{M(i)k}取为零算子.令

1 主要结果
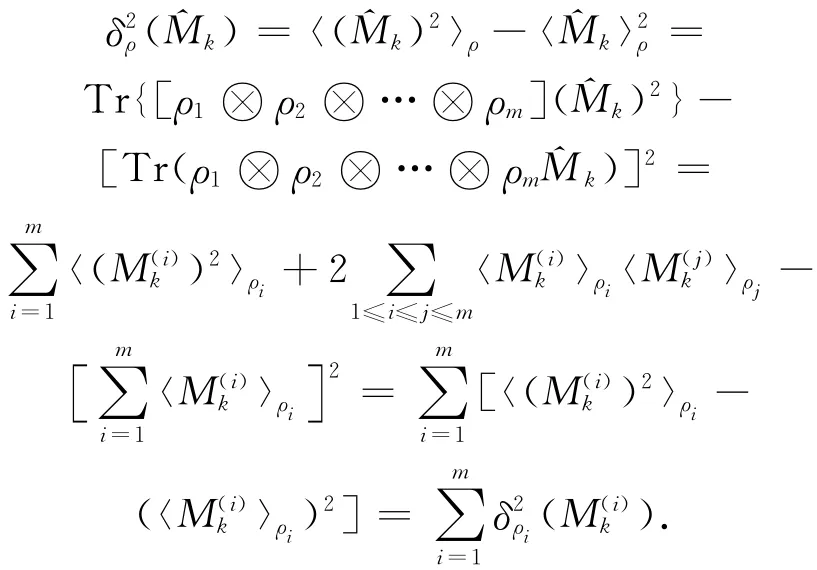
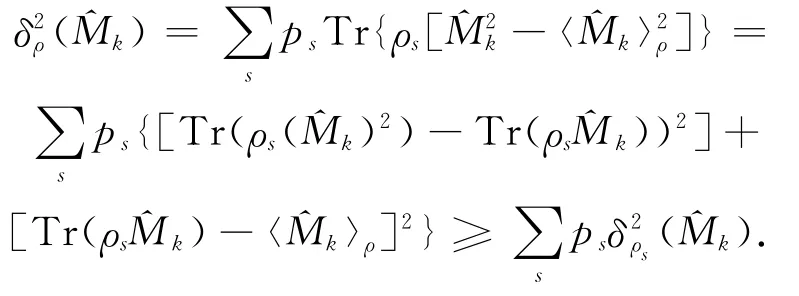
证毕.
例1 设H =HA⊗HB⊗HC,dimHA=dimHB=dimHC=2,考虑三量子比特的Werner态取HA,HB,HC的局部正交可观测量集合为记

例2 设H =HA⊗HB⊗HC,dimHA=dimHB=dimHC=2,考虑三量子比特的Werner态和GHZ态的组合([1]):ρt=t|GHZ〉〈GHZ|+取HA,HB,HC的 局 部 正 交 可 观 测 量 集 合 为可以获得注意到当0≤t≤1,总有
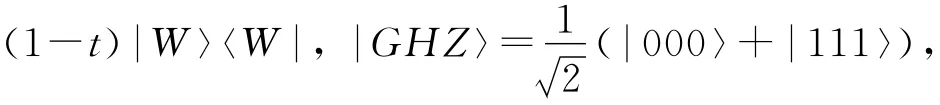

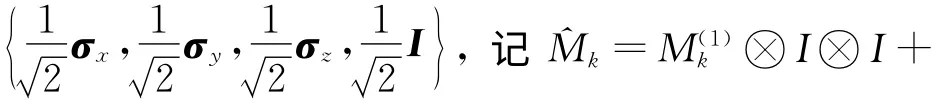

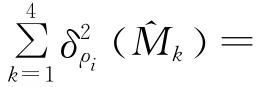


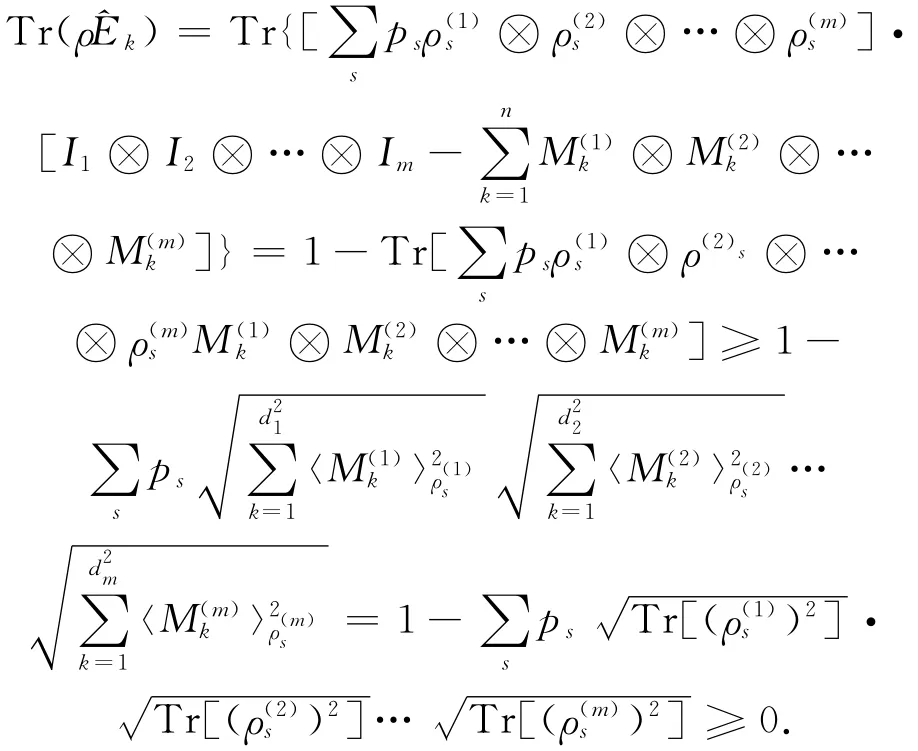
证毕.
例3 仍然考虑例2给出的态ρt,取HA,HB,HC的 局 部 正 交 可 观 测 量 集 合 为
在Hi上的不可交换的可观测量(i=1,2,…,m),

证毕.
引 理1[9]设为d2个 作 用 在H 上 的 不可交换的可观测量,则

式中:I(ρi,Mk)(i=1,2)的定义如式(4).
证明 设ρ=∑spsρs 为一混合态且全可分,设注意到根据引理1,有

[1]Nielsen M A,Chuang I L.Quantum computation and quantum information[M].Cambridge:Cambridge University Press,2000.
[2]Horodecki M,Horodecki P,Horodecki R.Separability of mixed states:Necessary and sufficient conditions[J].Phys Lett A,1996(223):1-14.
[3]Chen K,Wu L A.A matrix realignment method for recognizing entanglement[J].Quant Inf Comput,2003(3):193-202.
[4]Nielsen M A,Kempe J.Separable states are more disordered globally than locally[J].Phys Rev Lett,2001(86):5184-5187.
[5]Horodecki P.Separability criterion and inseparable mixed states with positive partial transposition[J].Phys Lett A,1997(232):333-339.
[6]Hou J C.A characterization of positive linear maps and criteria of entanglement for quantum states[J].Journal of Physics A:Mathematical and Theoretical,2010(43),385201.
[7]Yan S Q,Hou J C.LPP elementary operator criterion of full separability for states in multipartite quantum systems[J].Journal of Physics A:Mathematical and Theoretical,2012(43):435303.
[8]Hofmann H F,Takeuchi S.Violation of local uncertainty relations as a signature of entanglement[J].Phys Rev A,2003(68):032103.
[9]Guhne O,Mechler M,Toth G,et al.Entanglement criteria based on local uncertainty relations are strictly stronger than the computable cross norm criterion[J].Phys Rev A,2006(74):010301.
[10]Ma Z H.Entanglement criterion based on skew information[J].arXiv,2009(8):1291.
[11]Wigner E P,Yanase M M.Information contents of distributions[J].Proc.Natl.Acad Sci,1963(49):910-918.
[12]Yu C S,Wu S X,Wang X G.Quantum correlation measure in arbitrary bipartite systems[J].Europhysics Letters.2014,107(1):1-6.
[13]Saboia A,Avelar A T,Walbom S P.Systematic construction of genuine multipartite entanglement criteria using uncertainty relations[J].arXiv,2014(7):7248.
[14]Guo J L,Wei J L,Qin W,et al.Examining quantum correlations in the XY spin chain by local quantum uncertainty[J]. Quantum Information Processing,2015,14(4):1-14.

