一类超临界椭圆方程组正解的存在性

康晓红，樊永生

（1．深圳职业技术学院 数理部，深圳518055；2．中北大学 计算机与控制工程学院，山西 太原030051）

0 引 言

设Ω 是n≥3维有界区域．讨论椭圆方程组方程组（1）的解的存在性一直是人们关心的主题，有大量的文献关注，如de Figueiredo－Felmer［1］及其所列参考文献．

从变分法的角度看，这是一类完全不定型椭圆方程组．近来，这类问题重新引起了关注．本文所关心的是f（x，u）与g（x，v）的非线性程度．

对于g＝vp，f＝uq（p，q＞1是实数），问题称为Lane－Emden方程组，存在关于p，q 的所谓临界双曲线，也叫临界Hardy－Littlewood－Sobolev曲线，该曲线方程为

对于位于这条曲线及以上的点（p，q）（式（2）将等号改为“＜”），问题（1）会出现Pohozaev障碍，即当Ω 为星形区域，对于曲线（2）及以上的点（p，q），问题（1）无非平凡解．参见Mitidieri［2］，与此相关的新近发展见Phan［3］，也见Li［4］及Ghergu－Tailiaferro－Verbitsky［5］．另 一 方 面，de Figueiredo［1］证明，对于曲线（2）下方的点（p，q）（在式（2）中将等号改为“＞”），却有非平凡解，这一结论对于较广的非线性情形也成立，参见文献［2，6－7］．

本文寻求超越Pohozaev障碍的条件．讨论模型化问题：Ω＝B 为n≥3维球域，p，q＞1是实数，参数α，β≥0．讨论下列问题正解的存在性问题（3）称为Henon 问题．本文主要结果是定理1，证明当（p，q）满足以下两个条件

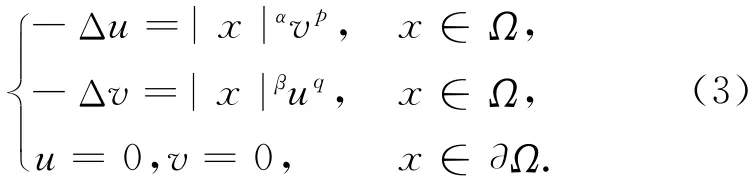
时，问题（3）具有一组正解（u，v）．条件（5）本质上是对α，β的限制，而条件（4）则是对Hardy－Littlewood－Sobolev临界双曲线（2）的一个超越．

本文完成后，我们查到Liu－Yang［8］有一个类似的结论，但该文有n≥5的维数限制，以及另一个比式（5）更苛刻的限制我们不知道这类限制是方法产生的抑或是本质的．

此 外， 文 献 D’Ambrosio－Mitidieri［9］与Fang［10］也讨论过相关的不存在性定理．

现在引进本文第一个重要引理．如不作特别说明，本文中Ω＝B 是球心在原点的n≥3 维球域．

记

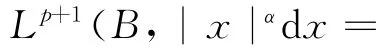
引理1（径向引理） 设u∈C1c（B），径向对称，1＜s＜n，α＞0，则

证明 见文献［11－13］．

引理2（嵌入定理） 设α＞0，s＞0，则对于

是连续紧嵌入．

证明 设u∈C1c（B）称函数，由引理1得（ρ＝

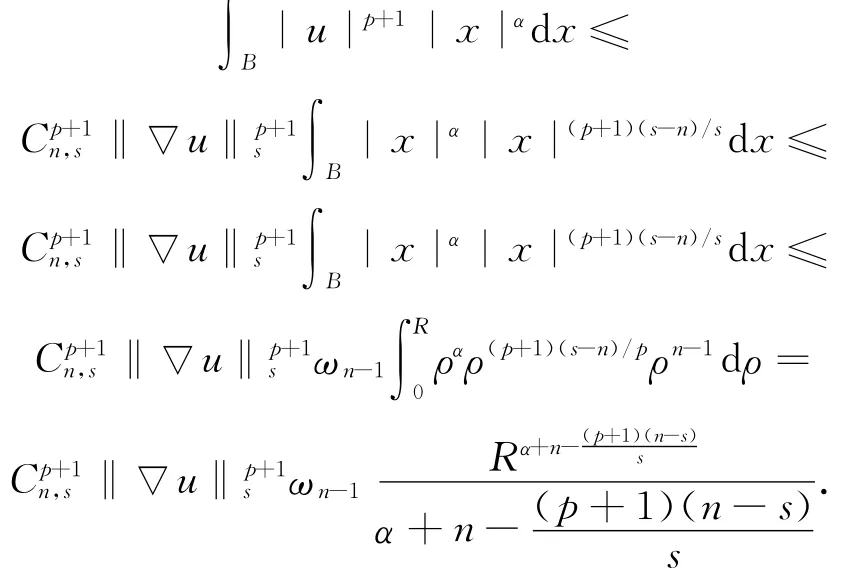
现在讨论问题（3），其对应的变分泛函为

如果p，q 增长不太大，则J（u，v）在H10（B）×H10（B）上是适定的．对于较大的p，q 则不然．有的作者使用分数阶Sobolev 空间来克服此困难，如Hulshof et al［7］及Liu－Yang［8］．

证明 由于式（5），不妨设

根据式（4），可取ε＞0充分小，使得

并取s＞0满足

根据式（6），0＜s＜1．而s的取法保证p＋1＜p＋

命题1 说 明，泛 函J（u，v）在SW1，s′0（B）×SW1，s0（B）上有定义，是良定的．下文中的s，s′均这样取定．但为下文方便，将s，s′的位置互换．

1 Sobolev映射

考虑定义在SW1，s0（B）×SW1，s′0（B）上的双线性泛函∫B▽u·▽v．给定u∈SW1，s0（B），设˜u∈SW1，s′0（B）满足

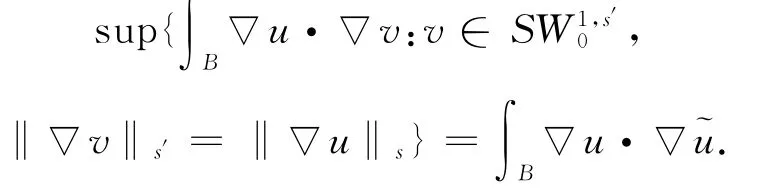
据SW1，s0（B）与SW1，s′0（B）的 一 致 凸 性，˜u ∈SW1，s′0（B）唯一存在．易见

映射u→˜u 是非线性的，但却是正齐次的：ρ˜u＝ρ˜u．

在E＝SW1，s0（B）×SW1，s′0（B）上定义Bnach流形

‖▽˜u‖2s′．

2 环绕结构及P．－S．序列的有界性

命 题2 存 在ρ ＞0 及σ ＞0 使 得 当‖（u，˜u‖E＝ρ时，J（u，˜u）≥σ．证明 这是初等的．也可参见文献［14－15］．固定元e∈SW1，s0（B），‖▽e‖s＝1．设R0＞0及R1＞0，记

命题3 存在正数R0，R1，使得对于任意z∈∂Q，有J（z）≤0，其中∂Q 表示Q 在R（e1，˜e1）˜＋E－中的边界．

先设R1＝1，

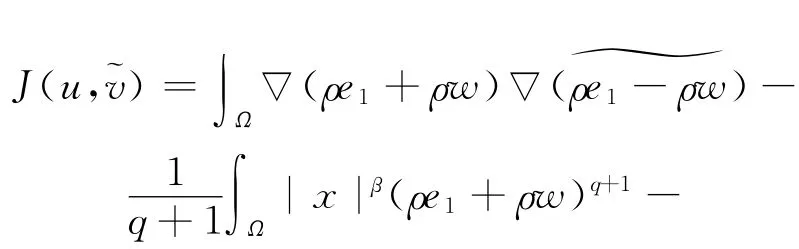
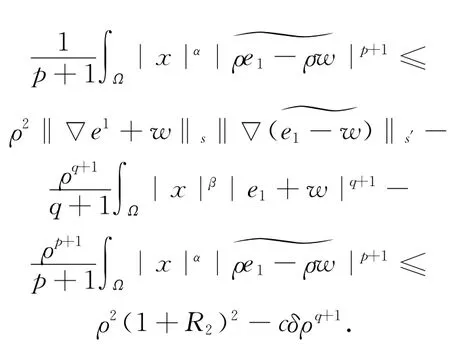
命题4 设zj＝（uj，˜vj）∈E 满足J（zj）有界及J′（zj）→0，则‖zj‖E有界．

证明 参见文献［15］．

3 有限维逼近

注意，泛函J 在无穷维流形E＋上正定，在无穷维流形E－上负定，故在E 上是强不定的，因而常规的环绕理论不适用．因此，采用有限维逼近法，Galerkin方法．

记｛ei｝为H10（B）的正交基底，由Laplace算子－Δ 在H10（B）中的特征函数构成．令

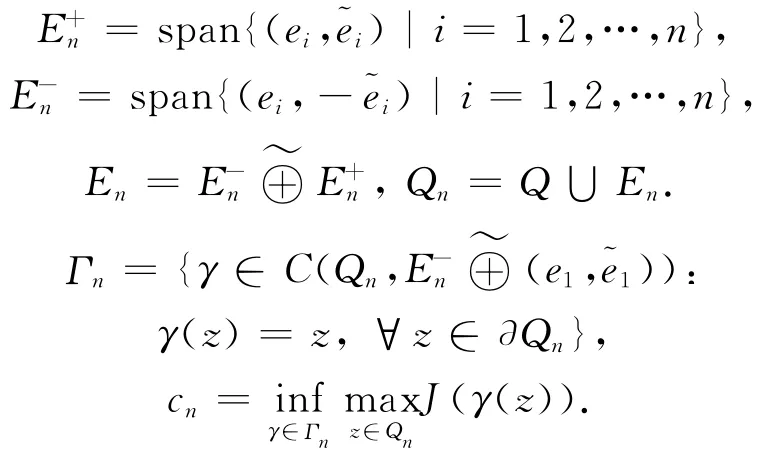
用标准变分原理得

定理1 设α，β≥0，1＜p，q＜∞且满足式（4）与（5），则问题（3）至少具有一组正解．

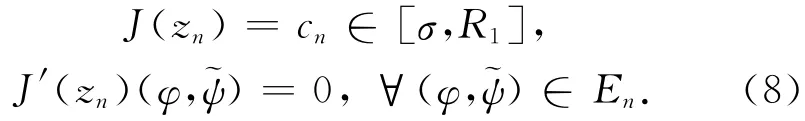
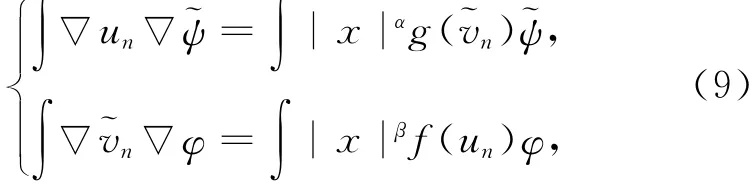
有

由P．－S．序列的有界性知，‖（un，˜vn‖E≤c．由自反性，存在（u，˜v）∈E，使得

故∀（φ，˜ψ）∈∩En＝E，

故（u，˜v）是方程组（3）的弱解．

现在证明（u，˜v）是非平凡解．用反证法，设若u＝0，则也有˜v＝0．设（u，˜v）＝（0，0）．在式（9）中令˜ψ＝˜vn，则有

这里用到了嵌入SW1，s0（B）→Lp＋1（B，｜x｜αdx）的紧致性．因此，J（un，˜vn）→0，与式（8）矛盾．故

［1］de Figueiredo D G，Felmer P．On superquadratic elliptic systems［J］．Trans Amer Math Soc．，1994（343）：99－116．

［2］Mitidieri E．A Rellich type identity and applications［J］．Comm Partial Diff Equations，1993（18）：125－151．

［3］Phan Q P．Liouville－type theorems and bounds of solutions for Hardy－Henon elliptic systems［J］．Adv．Differential Equations，2012（17）：605－634．

［4］Li Y．Optimal conditions for a priory estimates for semilinear elliptic systems with two components［J］．Nonlinear Analysis，2010（72）：1850－1864．

［5］Ghergu M，Tailiaferro S，Verbitsky I．Pointwise bounds and blow－up for systems of semilinear elliptic inequalities at an isolated singularity via nonlinear potential estimates［J］．arXiv，2014（2）：0113．

［6］R．van der Vorst．Variational identities and applications to differential systems［J］．Arch Rat Mech Anal，1991（116）：375－398．

［7］Hulshof J，Mitidieri E，van der Vorst R．Strongly indefinite systems with critical Sobolev exponents［J］．Trans Amer Math Soc，1998（350）：2349－2365．

［8］Liu F，Yang J．Nontrival solutions of Hardy－Henon type elliptic systems．Acta mathematica Scientia，2007（27B）：673－688．

［9］L．D’Ambrosio and E．Mitidieri，Entire solutions of quasilinear elliptic systems on Carnot Groups，Proc．Steklov Inst．Math．，2013，283（1）：3－19．

［10］Fang F．Nontrival solutions for semilinear elliptic systems via Orlicz－Sobolev theory［J］．arXiv，2013（7）：7362．

［11］王文智．变分法与临界非线性［M］．厦门：厦门大学出版社，2010．

［12］王文智，康晓红．基本巴拿赫空间［M］．广州：华南理工大学出版社，2013．

［13］Wang W Z．Sobolev embeddings involving symmetry［J］．Bull Sc Math，2006（130）：269－278．

［14］钟承奎，范先令，陈文源．非线性泛函分析引论［M］．兰州：兰州大学出版社，1998．

［15］Ruf B．Lorentz Spaces and nonlinear elliptic systems．progress in nonlinear differential equations and their applications［M］．Boston：Birkhauser，2006．