2018年武汉大学自主招生数学考试第4题的新证与加强

(大冶市第一中学,湖北 大冶 435100)

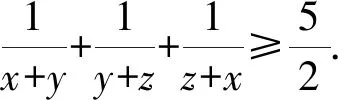
(2018年武汉大学自主招生数学试题第4题)

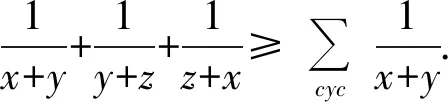
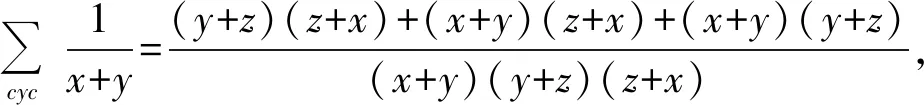
及

(y+z)(z+x)+(x+y)(z+x)+(x+y)(y+z)=x2+y2+z2+3(xy+yz+zx)，

(x+y)(y+z)(z+x)=(x+y+z)(xy+yz+zx)-xyz,

又xy+yz+xz=1，可得

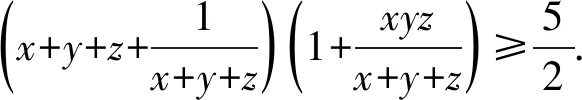
(1)

1)若x+y+z≥2，则

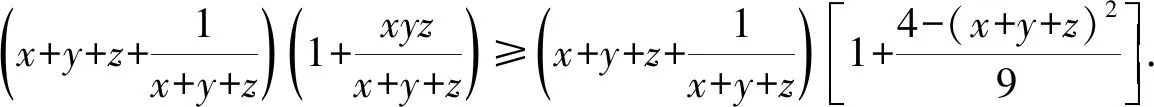
欲证不等式(1)成立只需证

上式⟺2[(x+y+z)2+1][13-(x+y+z)2]≥45(x+y+z)⟺

2(x+y+z)4-24(x+y+z)2+45(x+y+z)-26≤0⟺

(x+y+z-2)[2(x+y+z)3+4(x+y+z)2-16(x+y+z)+13]≤0⟺

2(x+y+z)3+4(x+y+z)2-16(x+y+z)+13≥0⟺

2(x+y+z)[(x+y+z)2-3]+(x+y+z)[4(x+y+z)-6]+13-4(x+y+z)≥0,

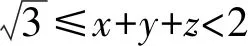
综合上述，可知不等式(1)成立，故所证不等式成立.

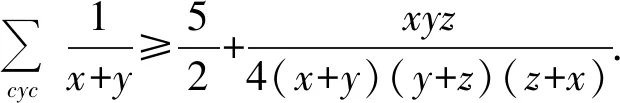
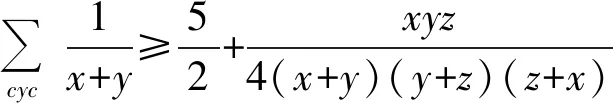
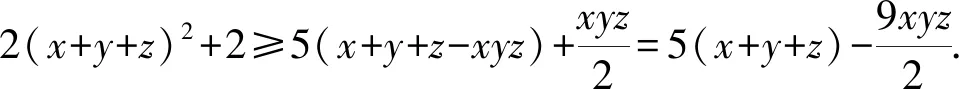
而(x+y+z-2)2≥0,将2(x+y+z)2≥8(x+y+z)-8代入上式后，只需证明

(2)

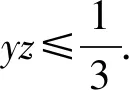
因此不等式(2)成立，加强1成立.

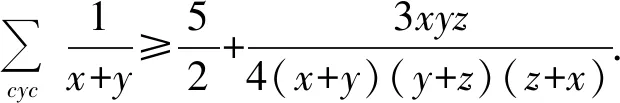
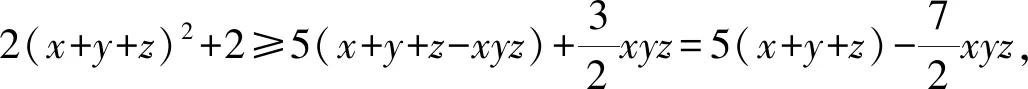
(3)

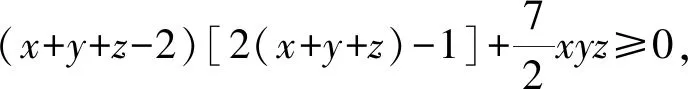
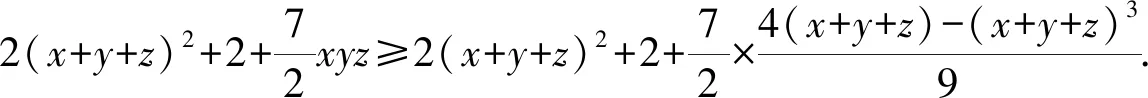
36(x+y+z)2+36+28(x+y+z)-7(x+y+z)3≥90(x+y+z),

亦即

(x+y+z-2)[7(x+y+z)2-22(x+y+z)+18]≤0，

只需证

7(x+y+z)2-22(x+y+z)+18≥0.

(4)

故不等式(4)成立，即加强2成立.

加强3已知x,y,z≥0,xy+yz+xz=1，求证：

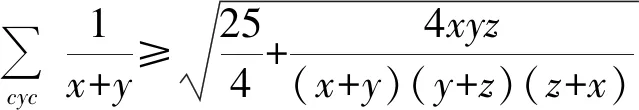
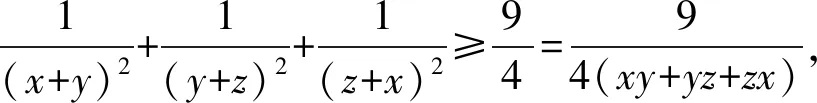
加强4已知x,y,z≥0，xy+yz+xz=1,求证：

证明令p=x+y+z，q=xy+yz+xz=1，r=xyz,则所求证式等价于

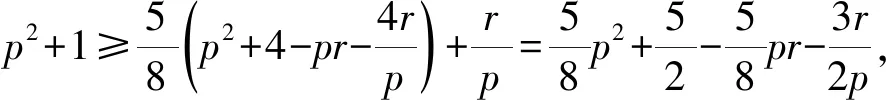
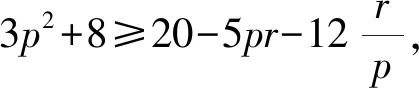
整理得

3p3+5p2r+12r≥12pq(其中q=xy+yz+zx=1).

由p2≥3可知3p3+5p2r+12r≥3p3+27r≥12pq(三元舒尔不等式),故加强4成立.