局域共振型周期结构振动带隙形成机理

李锁斌,窦益华,陈天宁,李冰,苏健军,张帆,崔潇骁

(1.西安石油大学机械工程学院,710065,西安;2.西安交通大学机械工程学院,710049,西安;3.西北工业大学航空学院,710072,西安;4.西安近代化学研究所,710065,西安;5.北京特种工程设计研究院,100028,北京)

近年来,关于弹性波或振动在周期结构中的传播研究已成为固体物理学、材料科学及工程技术科学领域里一个热点[1]。由于周期结构对弹性波或振动传播过程具有独特的调控作用——弹性波或振动带隙特性[2],即当弹性波或振动通过时,带隙内的波或振动会被抑制,因此研究这一特性的物理本质将为凝聚态物理学中复杂物理现象(负质量/折射、声子聚焦等)的研究提拱理论支撑,为新型多功能材料(隐身/波导材料等)的设计提供新的方法,为工程技术科学中新型功能结构(结构隔振/减振等)的研制提供新思路[3-4]。

依据弹性波或振动带隙形成机理,周期结构可分为布拉格散射型[5]和局域共振型[6]两种,布拉格散射型周期结构因其带隙主要由散射体对波的各种周期性调制产生,使得带隙波长和结构尺寸处于同一数量级,很难实现小尺寸控制大波长。局域共振型周期结构的带隙主要由振子的共振引起,带隙波长较小,可以实现小尺寸控制大波长,有望实现低频应用,如工程结构的振动控制。

迄今,人们对于局域共振型周期结构的带隙形成机理的本质认识还不够透彻,解释依然较为笼统,虽然学界对局域共振带隙的形成机理已达成共识[7-20],即振子的局域共振模态与基体模态发生相互耦合致使带隙形成,但对振动带隙产生的详细过程还缺乏全面深入的认识,使得目前只能解释带隙是如何打开的,却不能进一步揭示带隙(或带宽)是如何形成的,即只是简单认为带隙的宽度取决于振子模态与基体模态的耦合强弱,但对于二者的耦合机制及其遵循的基本准则没有详细论证,尚未有关于带隙形成机理的明确的统一表征模式,因此对局域共振型周期结构的带隙特性还无法实现主动设计。

针对上述问题,本文以局域共振型周期结构为对象,研究带隙详细形成过程机制,阐明带隙形成机理。本文的研究思路为:提出带隙形成的基础理论假说,据此建立带隙形成理论模型,依此阐明带隙形成过程机制,并以典型二维周期结构的振动带隙形成过程为例对所提出的理论及其模型进行验证,最终提出并阐明局域共振型周期结构的振动带隙形成机理。

1 振动带隙形成的基础理论假设

基于动力学理论,给出局域共振型周期结构振动带隙形成的基础理论假设,为提出带隙机理奠定理论基础。对一个n自由度系统,当施加激励feiωxt时,其物理坐标下的动力学耦合方程为

(1)

式中M、K分别为质量和刚度矩阵,表示为

(2)

通过化简得到系统固有特性的表征式

|K-ω2M|=0

(3)

式中:ω=[ω1,ω2,…,ωn]为n阶固有频率。n阶振型A表示为

(4)

依据模态分析原理,将式(4)代入式(2),对质量和刚度矩阵进行正则化,得到正则质量和正则刚度矩阵MP和KP如下

(5)

(6)

于是系统在模态坐标下的解耦动力学方程为

(7)

式中:xp为系统在模态坐标下的响应。质点i的响应xpi表示为

(8)

进而,得到系统在物理坐标中的响应为

x=Apxp

(9)

因此,质点i在物理坐标下的响应为

(10)

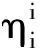
(11)

2 振动带隙形成机理模型

基于提出的基础理论假设,建立振动带隙形成的理论模型,原理如图1所示。

图1 局域共振型周期结构带隙形成的理论模型

将基体等效为具有广义质量m1、广义转动惯量I1和广义刚度k1的等效系统1。其中,广义集中质量沿空间x、y、z这3个方向的运动模式x1、y1、z1分别对应着3种广义平移振动模式,广义集中惯量沿3个坐标轴的转动模式α1、β1、γ1分别对应着3种广义转动振动模式,系统1有6种广义振动模式。将振子等效为具有广义质量m2、广义转动惯量I2和广义刚度k2的等效系统2。其中,广义集中质量沿x、y、z3个方向的运动模式x2、y2、z2分别对应着3种广义平移振动模式,广义集中惯量沿3个坐标轴的转动模式α2、β2、γ2分别对应着3种广义转动振动模式,系统2有6种广义振动模式。于是,局域共振型周期结构中可传播6种广义波模式。基于带隙形成的基础理论假设和模型,得到局域共振型周期结构的广义振动模式也即基体的传播模式的表征式

(12)

(13)

(14)

(15)

(16)

(17)

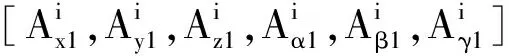
(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

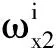
3 振动带隙形成过程机理

依据上述模型,提出局域共振型周期结构中振动带隙详细形成过程机制如下。

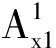
图2 局域共振型周期结构子带隙形成过程原理

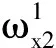
(26)

式中k2和m2分别为振子在该阶主模态的等效刚度和等效质量。带宽由振子对基体主模态的抑制力强弱决定,抑制力为

(27)

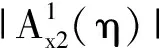
(28)

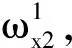
(3)基体中存在6种广义振动模式,各种模式由其对应的12阶广义模态依据模态叠加原理形成的主模态主导形成;振子主模态主导的振子模式依据模态参与因子通过抑制或释放基体传播模式的方式决定着振动带隙的形成,即当振子主模态抑制广义振动传播模式时,形成了只能抑制该传播模式的子带隙;6种传播模式对应6条广义子带隙,相互叠加形成完全振动带隙,带隙内6种广义振动或传播模式均被抑制。

4 振动带隙形成机理验证

以典型局域共振型周期板结构[12]为例,验证上述理论。

该结构是通过在均匀板上周期布置一振子阵列而形成的二维局域共振型周期结构,原理如图3所示。图3a表示结构形貌;图3b表示周期单元,振子由软橡胶柱A和钢柱B构成,二者高度分别为hA和hB,直径均为d,基板厚为e,单元边长为a;图3c表示第一布里渊区。

(a)结构形貌 (b)周期单元 (c)第一布里渊区图3 典型局域共振型周期板结构

采用有限元方法,通过Comsol Metaphysics 3.5a软件计算能带。计算中结构的几何、材料参数与文献[20]相同,最终得到结果如图4所示。从图4可以看出,在给定频率范围内存在一条完全带隙(图4a中频率为300～450 Hz区域),两条子带隙2-x、2-y模式弹性波带隙(图4b中频率分别为100～200 Hz和300～450 Hz区域),一条子带隙1-z模式弹性波带隙(图4c中频率为300～850 Hz区域)。

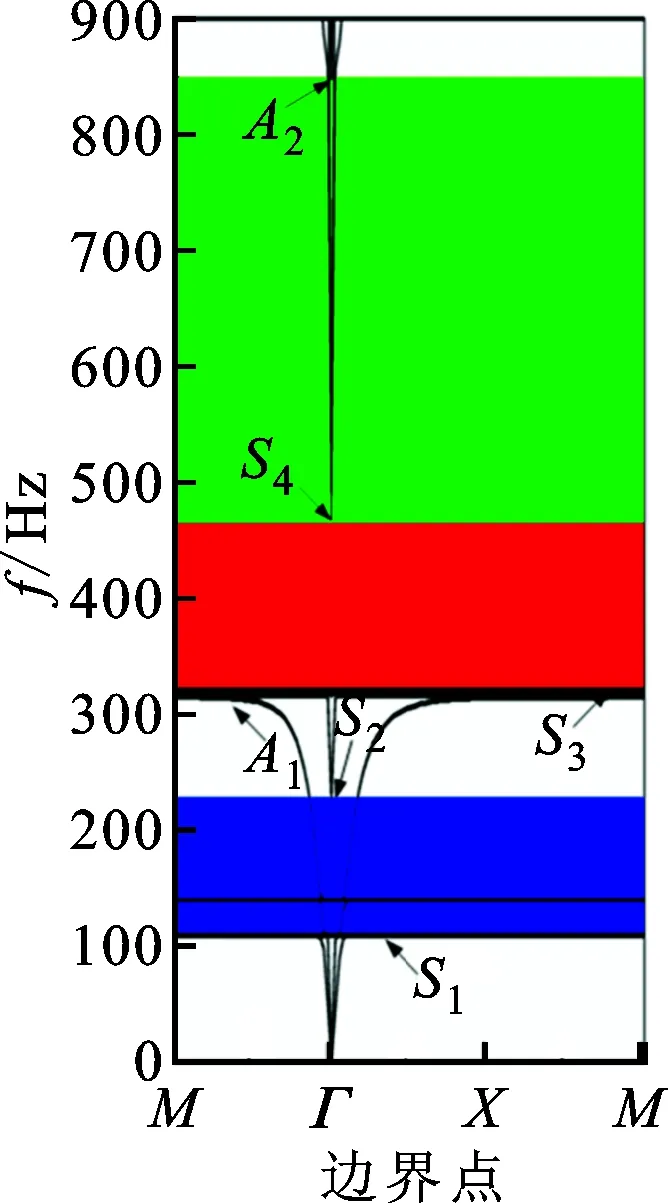
(a)完全带隙

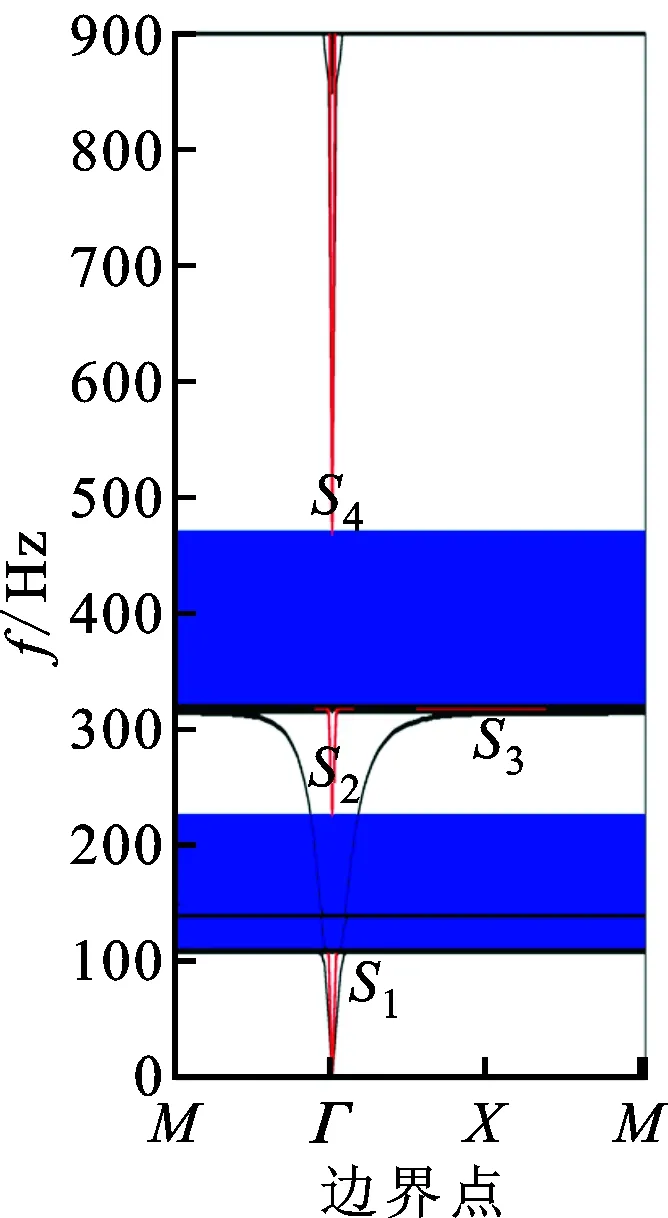
(b)子带隙2

(c)子带隙1

4.1 子带隙1-z模式带隙形成机理验证

将子带隙1局部放大,结果如图5b所示。

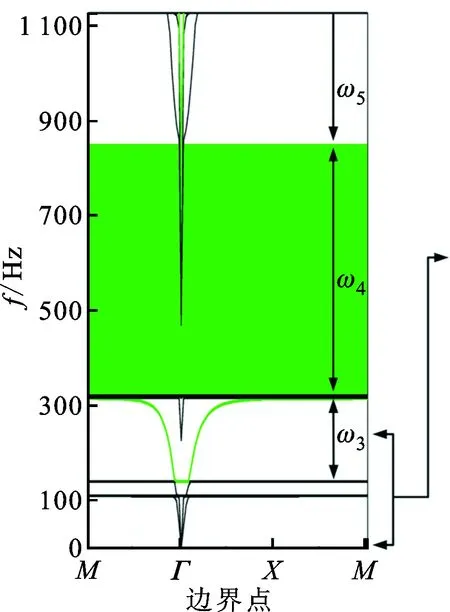
(a)z模式能带图

(b)z模式能带局部放大图

提取能带曲线上典型点对应的单元振动模式,如图6所示。

图6 单元的z模式振动

子带隙1-z模式带隙形成的详细过程如下。

(1)当激励频率ω从0趋于120 Hz,即区间ω1,板波模态1被激发放大成为基板主模态,主导基板响应,横向波(面外波)按该模式传播,不发生衰减(有限结构中波传播过程如图7中过程(1)所示),无子带隙1形成。

(2)当激励频率ω=120 Hz,模态6被激发放大成为振子主模态,但其振动模式为旋转运动,与板波主模态不耦合,给基板沿垂直方向的作用力为零,未能抑制基板模式1,振动按模式1继续传播,子带隙1未形成或者带宽为0。

(3)当激励频率ω从120 Hz趋近140 Hz,即ω2区间,板波模态2被激发放大为基板主模态,主导基板响应,横波按该模式传播,无子带隙1形成。

(4)当激励频率ω=140 Hz,模态6被激发放大成为振子主模态,子带隙1未形成或者带宽为0。

(5)当激励频率ω从140 Hz趋于320 Hz,即ω3区间,板波模态3被激发放大为基板主模态,主导基板响应,横波按该模式传播,无子带隙1。

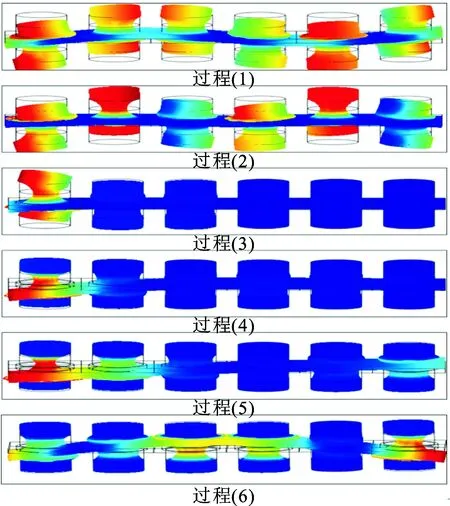
图7 有限周期结构中z模式振动的传播过程

(6)当激励频率ω=320 Hz,模态4被激发放大为振子主模态,主导振子振子沿垂直于板的方向运动,抑制了基板主模态,板内无z振动模式,横波无法传播,第一条子带隙1打开(传播过程如图7中过程(2)所示)。开带位置为振子主模态4的固频,据带隙理论,振子在该阶主模态的等效质量为

m=πρBhB(d/2)2

(29)

式中:ρB为振子B的密度。对于振子A,沿z方向的正应力与正应变成正比,即

(30)

式中:Δz为振子A在z方向上的形变;EA为振子A的弹性模量;振子在该阶主模态的等效刚度为

(31)

于是子带隙1的起始位置频率为

(32)

从而验证了通过设计振子主模态的等效刚度和等效质量,可对带隙起始位置进行主动设计。

(7)当激励频率ω从320 Hz趋于850 Hz,即ω4区间内,模态4依然为振子主模态,主导振子运动。随着激励频率远离模态4的固频,其模态参与因子变小,振子对基体主模态的抑制变弱,表现为远离开带位置处,横向波的衰减变小,但此区域内,板的z模式依旧被抑制(传播过程如图7中过程(3)(4)所示),形成子带隙1,带宽为ω4。据带隙理论,振子在该阶主模态对基体主模态的抑制力为

(33)

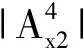
(8)当激励频率ω=850 Hz,模态4的参与因子变小,其对振子的主导变弱,板波模态5被激发放大成为基板主模态,主导基板响应,横向波按此模式传播(有限结构中波的传播过程如图7中过程(5)所示),子带隙1关闭。

(9)当激励频率ω大于850 Hz,即ω5区间,板波模态5保持为基板主模态,主导基板响应,横向波按此模式传播(传播过程如图7中过程(6)所示),子带隙1消失。

4.2 子带隙2-x、2-y模式带隙形成机理验证

将子带隙2局部放大,结果如图8b所示。

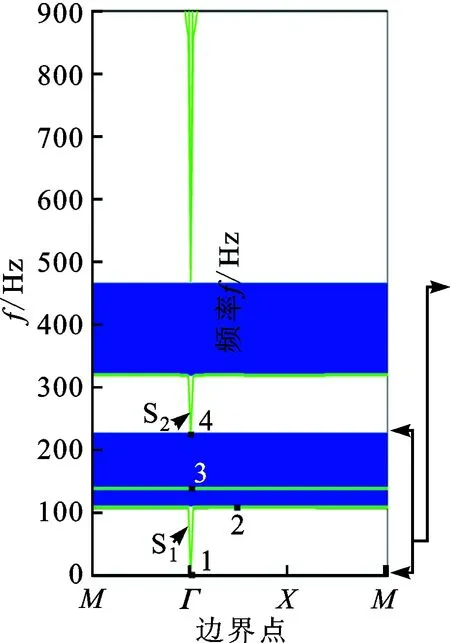
(a)x、y模式能带图

(b)x、y模式能带局部放大图

提取子带隙2能带上典型点对应的单元振动模式,如图9所示。

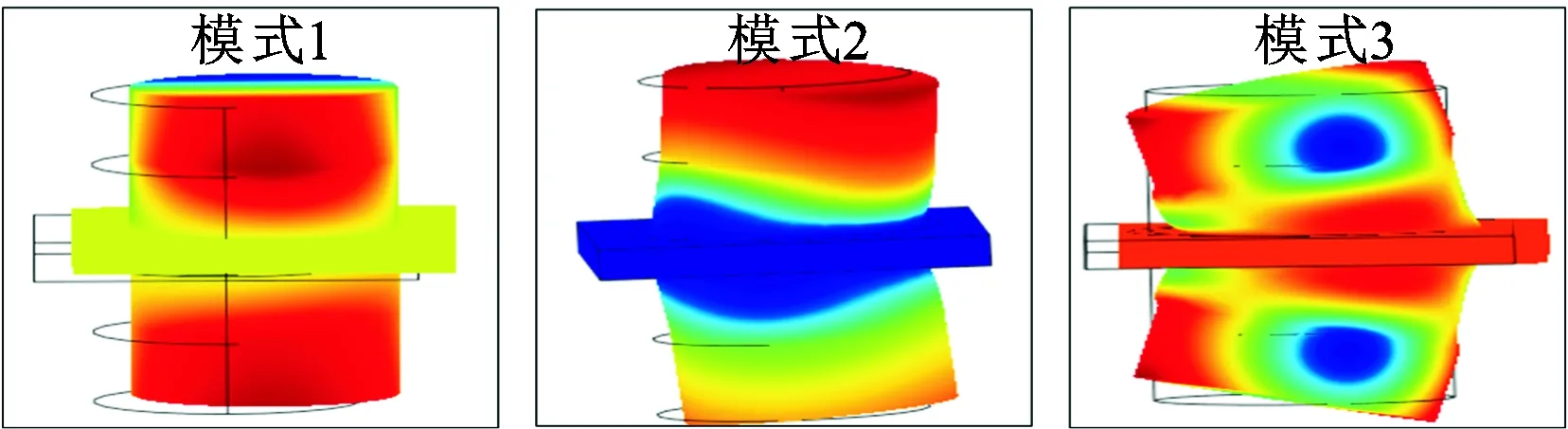
图9 单元x、y模式振动

子带隙2-x、2-y模式带隙形成详细过程如下。

(1)当激励频率ω从0趋于120 Hz,即ω1区间,板波x、y振动模态1被激发放大成为基板主模态,主导基板响应,纵波按该模式传播,不发生衰减(传播过程如图10中过程(1)所示),无子带隙2形成。

图10 有限结构中x、y模式振动传播过程

(2)当激励频率ω从120 Hz趋于230 Hz,即ω2区间,模态2被激发放大为振子主模态,主导振子运动,抑制基板主模态,纵波无法传播(传播过程如图10中过程(2)和(3)所示,),子带隙2形成。

(3)当激励频率ω从230 Hz增大,即ω3区间,板波x、y振动模态3被激发放大成为基板主模态,主导基板响应,纵向波按此模式传播,不发生衰减(传播过程如图10中过程(4)所示),无子带隙2形成。

4.3 完全带隙形成机理验证

依据上述分析可知:基体振动模式由其各阶模态依据模型叠加原理形成的主模态主导形成;振子主模态依据模态参与因子通过抑制基体主模态的方式决定着振动带隙的形成,即当振子主模态抑制基体的主模态时,形成了只能抑制该模式的子带隙,子带隙相互叠加,形成完全带隙。验证模型中,完全带隙(见图4a)仅由子带隙1和2叠加而成。因此,说明本文提出的局域共振型周期结构振动带隙形成的基础理论假说和依此建立的带隙形成理论模型,以及据此揭示的振动带隙形成机理,是合理的。据此,通过设计振子主模态等效刚度和等效质量,可对带隙打开位置进行主动设计,通过设计振子主模态等效刚度可对带宽进行主动设计。

5 结 论

本文的主要工作和结论如下:

(1)基于动力学原理,给出了局域共振型周期结构振动带隙形成的基础理论,据此建立了带隙形成的理论模型,依此模型阐明了带隙形成机理并通过局域共振型周期板中带隙形成时弹性波与结构的相互作用机制验证了该理论;

(2)局域共振型周期结构存在6种广义振动模式,各模式由广义模态依据模态叠加原理形成的主模态主导形成,振子主模态依据模态参与因子通过抑制或释放基体主模态的方式决定着振动带隙的形成;

(3)带隙特性主要由振子主模态的等效刚度和等效质量决定,通过设计振子主模态的等效刚度和等效质量,可对带隙的打开位置频率进行主动设计,通过设计振子主模态的等效刚度,可初步对带隙的宽度进行主动设计。

本文研究为工程结构的减振技术提供了新方法的理论基础,并为周期结构带隙理论研究和带隙特性主动设计奠定了基础,完善了周期结构的基本理论。