改进的6σ设计的螺旋锥齿轮加工参数反调修正方法
彭山东,丁撼,唐进元
(1.中南大学高性能复杂制造国家重点实验室,410083,长沙;2.中南大学机电工程学院,410083,长沙)
螺旋锥齿轮由于具有承载能力大、传动比大、重合度高且能传递空间相交轴和交错轴之间的动力等特点,成为航空航天、汽车、工程机械等领域中动力传递的关键部件。螺旋锥齿轮的形状和性能对设备的使用寿命甚至安全性能有着至关重要的影响[1],因此关于螺旋锥齿轮的形性协同设计与制造是很有必要的。Artoni和Gabiccini考虑了齿面接触印痕的系统优化,并且基于齿面ease-off修正研究了传动误差的变化规律[2];Ding等提出了多目标函数优化系统,研究了不确定载荷对螺旋锥齿轮加载接触性能的影响[3-6];Deng等通过将齿轮制造技术与网络、信息和管理相结合,建立了基于网络的螺旋锥齿轮制造模型[7]。随着螺旋锥齿轮技术的发展,形性协同制造技术已经通过现代信息和自动化技术相关联而得到快速发展。Yang等利用web服务技术提出了一种新颖的信息集成服务平台,可为齿轮的网络化制造提供更好的服务和支持[8-9];Fung等通过将质量功能部署(QFD)、层次分析和模糊集理论的原理融合到混合系统中,可以确定齿轮设计的目标[10]。但是,由于螺旋锥齿轮形性协同制造系统涉及到实际齿轮加工、真实齿轮测量、加工参数反调等诸多环节,其整个系统流程繁杂而且稳定性差[11],尤其以通用加工参数为驱动载体的智能化自动识别、控制及反馈过程,需要充分考虑整个设计流程、决策与处理、数值求解算法的协同匹配及优化关系,实现整个系统的快速高效高质量的参数驱动[5]。因此,本文在国内外有关齿轮形性协同制造的基础上,提出了一种改进的定义-测量-分析-改进-控制(DMAIC)框架,根据改进的参数驱动关系形成改进的6σ设计流程;同时引入鲁棒性多目标反调优化方法,构建螺旋锥齿轮形性协同制造的多目标反调优化(MOO)模型,利用模糊QFD方法[12]将客户对齿轮产品的需求(VOC)反馈转化为相应的产品质量信息(CTQ),建立相应的质量屋(HOQ),并采用MOO求解方法[13]求解MOO模型,得到加工参数对接触性能的敏感性系数,结合组成敏感性系数矩阵,分析得到基于6σ设计的加工参数反调量,保证齿面接触性能评价项能够满足所设定的目标要求,实现整个螺旋锥齿轮形性协同制造的智能参数驱动;并以一对航空用螺旋锥齿轮为例,采用MOO方法对其进行基于6σ鲁棒性的MOO反调决策与优化,得到了加工参数的反调量和齿面接触性能的评价项参数值。
1 加工参数驱动决策的流程优化设计
1.1 改进的DMAIC框架
在基于6σ设计的螺旋锥齿轮形性协同制造智能参数驱动决策与处理中,存在着依托于有限元仿真齿面载荷接触分析(LTCA)平台的设计流程复杂、计算鲁棒性差等问题。传统的基于6σ的设计流程主要包括定义、测量、分析、设计和验证(DMADV)[5]等过程,其流程方案繁杂且稳健性较低,一旦框架不满足产品的设计要求时,就需重新寻找问题来源进行流程并进一步优化设计流程,提高决策处理的效率和整个流程的鲁棒性。本文基于目前的6σ设计研究成果,区别于DMADV框架,给出了一个改进的基本框架,包括定义、测量、分析、改进和控制(DMAIC),如图1所示。在传统流程中的设计阶段给出了改进方案,主要是考虑整个参数驱动系统的智能化程度和鲁棒性,提出了基于LTCA的物理性能评价的直接参数驱动函数关系[14],并且考虑了几何与物理性能协同优化的MOO加工参数反调过程,以此完成基于改进的6σ设计的螺旋锥齿轮形性协同制造方案设计。MOO反调模型中,f(M,X,Z)描述系统响应y,它是初始输入信号M、设计因子X和噪声因子Z的函数。对于输入信号M,加工参数被用作协同制造系统过程中的设计变量。
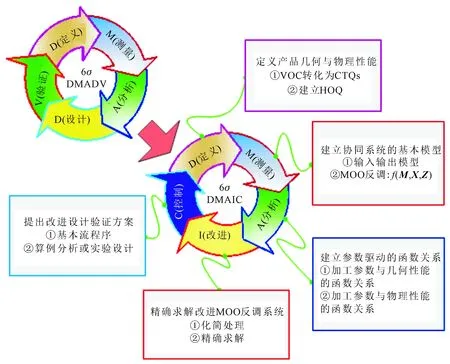
图1 形性协同系统的改进的6σ设计基本框架
1.2 改进的参数驱动关系
在整个螺旋锥齿轮形性协同制造的智能参数驱动决策过程中,对于性能评价项与加工参数的函数关系,将采用精确的函数求解方式完成其关联规律的直接参数驱动表达。首先,建立加工参数与几何性能评价项的函数关系,其参数驱动表达式为
(1)
式中:h表示残余ease-off齿面形貌,是螺旋锥齿轮几何性能评价项;M为初始加工参数;M*为MOO反调后的精确加工参数。

图2 螺旋锥齿轮精确有限元模型
对于加工参数与物理性能评价项的直接参数驱动关系,本文主要利用了齿面载荷接触分析方法[5]。如图2所示,建立螺旋锥齿轮的有限元模型,考虑齿面接触受力平衡与变形协调条件[15],就可以完成齿面物理评价项关于加工参数的函数关系表达,直接构建其多目标函数
(2)
式中:CPMAX是最大接触压力;LTEMAX是最大传动误差;CR是齿轮传动的重合度;η是齿轮的效率。具体的多目标函数关系构建可参考文献[4-5]。
式(2)联立子目标函数f1,可以构成5个目标函数协同的多目标优化系统,一次完成整个产品性能评价项的直接参数驱动决策与优化。
2 改进的6σ设计的基本流程
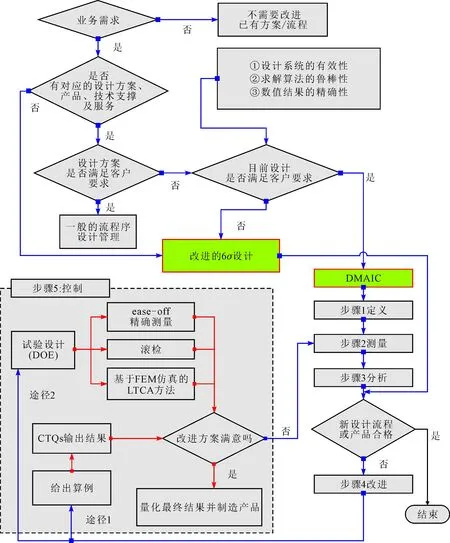
图3 基于改进的6σ设计的协同制造的参数驱动流程
为了满足螺旋锥齿轮产品的客户需求,本文提出了考虑几何与物理性能协同优化的改进的6σ设计方案。基于改进的6σ设计的螺旋锥齿轮形性协同制造基本流程如图3所示,与现有的基于DMADV框架的设计流程不同,改进的设计流程引入了MOO加工参数反调设计方法。提出的MOO加工参数反调是一个考虑接触性能和多个加工参数相互耦合作用的复杂系统[16-17]。建立的反调模型的强烈非线性[18]、子目标优化函数之间耦合性、迭代计算的收敛性等都将会较大程度地影响整个设计结果的鲁棒性。因此,为了保证结果数据的可靠性与精度,需提供合适的决策与优化方案,保证参数驱动设计与形性协同制造之间的关联性,必须同时满足所设定的几何和物理性能评价指标。
3 基于6σ鲁棒性MOO反调的决策与优化
在当前齿轮产品的设计与制造中,满足客户要求始终是设计者和制造者追求的目标之一。为了更好地将客户对齿轮产品的需求(VOC,设为VOC)反馈转化为相应的产品质量信息(CTQ),并保证其精确性和实用性,本文采用模糊QFD的方法[12],同时匹配基于模糊QFD的螺旋锥齿轮形性协同制造的智能参数驱动决策与优化方案。该模糊QFD过程可表示为[19]
X:VOC⊆R|→CTQs⊆R|→X=
[X1,X2,X3,X4,X5]=
[ω1hRMSE,ω2LTEMAX,ω3CPMAX,ω4CR,ω5η]
(3)
式中:wi(i=1,2,…,5)是客户需求项的最终权重因子,可以利用在模糊期望值算子中模糊权重平均值法来确定,详细的过程可参考文献[19]。
对于所提出的设计方法,选择以下几何和物理性能评价指标:①残余ease-off的均方根误差hRSME的最小化,是螺旋锥齿轮设计的传统几何性能目标评估项;②最大齿面接触压力CPMAX的最小化,可以提高强度、降低齿轮破坏形式的风险;③最大加载传动误差(LTEMAX)的最小化,可以减少齿轮传动在其主要包括噪声和振动的工况下的振动激励;④重合度CR的最大化,可以提高齿轮啮合强度,降低齿轮传动的冲击频率;⑤机械效率η最大化,可以预测摩擦功率损失和燃料经济性。
3.1 MOO基本模型
螺旋锥齿轮形性协同制造的参数驱动设计中,最核心的内容就是考虑几何和物理性能的MOO加工参数反调。根据实际加工精度可以预设齿面ease-off,即基本齿面与目标齿面沿法向方向的偏差值,同时考虑齿面物理性能评价项的多目标优化(MOO)方法,依次确定目标齿面,然后以机床加工参数为设计变量来考虑设计齿面与目标齿面的逼近,实际上表达的是一个齿面误差无穷小的数值优化过程,其目标函数可以表示为
(4)
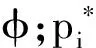
(5)
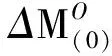
由于方程式(4)具有强烈非线性,可以转为关于加工参数的非线性最小二乘问题
(6)
式中:P是齿面ease-off要求的精度阈值,一般是一个区间范围,可以人为预设或者由客户要求。
3.2 6σ鲁棒性优化的MOO求解算法
本文所采用的鲁棒性优化计算方法可写成[13]
minF(uy(X),σy(X))
s.t.gi(uy(X),σy(X))≤0,i=1,2,…,m
XL+nσX≤uX≤XU-nσX
(7)
式中:X为设计因子;XU和XL分别为X的上、下边界;m为约束条件数;F为性能评价项的均值和标准偏差的目标函数;n为期望的σ水平。
针对上述提出的MOO基本模型,引入6σ鲁棒性优化设计方法,得到了基于6σ设计方法的MOO模型。为了保证结果数据的可靠性与精度,避免多个加工参数之间的耦合作用,需要求解齿面误差对加工参数的敏感性系数矩阵。根据敏感性系数矩阵判断加工参数对齿面误差的影响大小,主要针对敏感性较大的加工参数进行择优反调修正,其中所用的敏感性系数矩阵表示为

(8)
式中:hi(x)表示齿面ease-off关于加工参数的函数;xj表示加工参数。基于建立的几何性能和物理性能的直接驱动关系,建立考虑形性协同的MOO模型,如下式
(9)
式中:σy为设计性能响应y的标准偏差,可由下式计算[12]
(10)
(11)
其中μy是性能响应y的平均值,σXi和σXj为第i个和第j个设计变量的标准偏差。
对于多目标参数反调优化问题,本文采用列文博格-马跨尔特(L-M)算法[20]进行求解,其迭代过程表达为

(12)
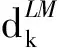
整个设计求解过程可以描述如下。
步骤1令K=0;
步骤2根据客户需求建立质量屋(HOQ),将VOC转化为CTQs;
步骤3建立如方程式(9)所示的MOO系统,并设定对应的目标约束条件;
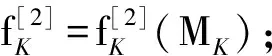
步骤5验证MK∈PS的实用性,通过与对应的CTQs的设定要求值比较;
步骤6通过求解计算来获得其他M个数值解;
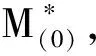
4 改进的6σ设计的螺旋锥齿轮加工参数反调计算
4.1 齿坯几何基本设计
本文以一对航空用螺旋锥齿轮为例,采用的齿坯设计参数和机床加工参数见表1、表2,其中将加工参数作为整个优化参数驱动过程的主要输入信号。考虑到几何与物理性能要求,采用提出的模糊FQD方法来将客户对齿轮的产品需求转换成产品质量信息,并以最终的几何与物理性能评价项作为性能目标驱动整个流程的求解。从动轮所受的扭矩载荷为257.693 N·m,从动轮转速为12 767 r/min。

表1 齿坯设计几何参数

表2 螺旋锥齿轮通用机床加工参数
4.2 计算结果及分析
为了节约计算时间并兼顾反调效果,本文主要针对接触点位置的参数进行反调修正。根据齿轮的加工方法不同,主要考虑径向刀位、滚比、床位、基本摇台角等加工参数的反调修正。基于提出的参数驱动决策与优化方法,计算各接触点位置时各加工参数对齿面ease-off的敏感性系数,组合得到各加工参数对齿面误差的敏感性系数矩阵。表3给出了接触点位置的加工参数的敏感性系数。根据提出的基于6σ鲁棒性优化的MOO反调求解算法,计算得到的精确加工参数和相应的加工参数反调量数值结果见表4。
图4给出了齿面接触点对加工参数的敏感性系数的拓扑图和分布图。分析对比各个加工参数敏感性系数可知,基本摇台角的敏感性系数最大,最大值接近5,滚比和机床安装根锥角的敏感性系数次之。因此,为了避免多个加工参数之间的耦合作用带来不必要的影响,降低反调计算的非线性,根据敏感性系数矩阵分析结果可知,主要针对基本摇台角、滚比、机床安装根锥角3个加工参数进行二次优化反调。通过二次优化反调后,可以得到优化反调的加工参数反调量,其参数的优化反调量见表4。

(a)拓扑图
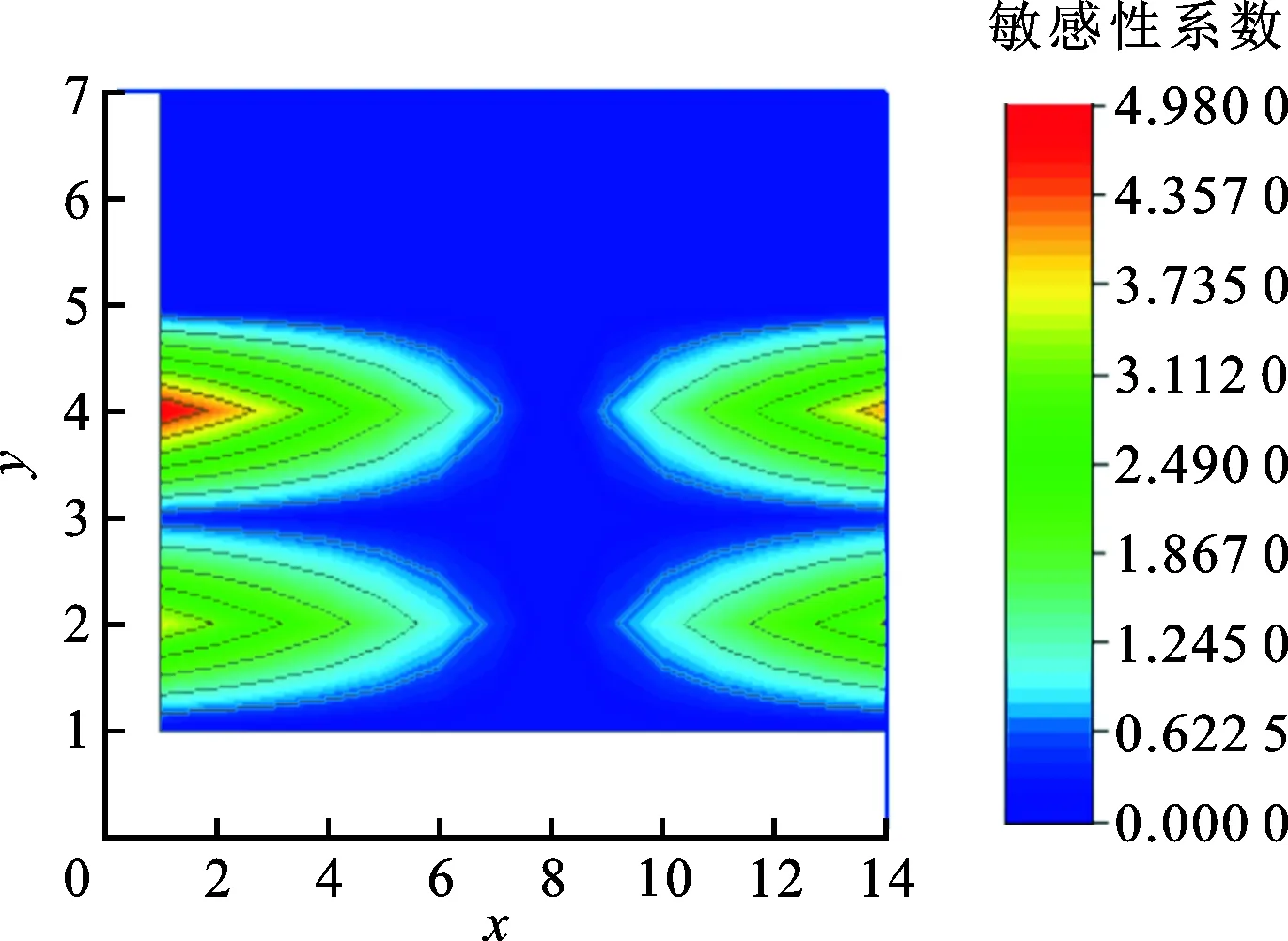
(b)分布图图4 齿面接触点的敏感性系数
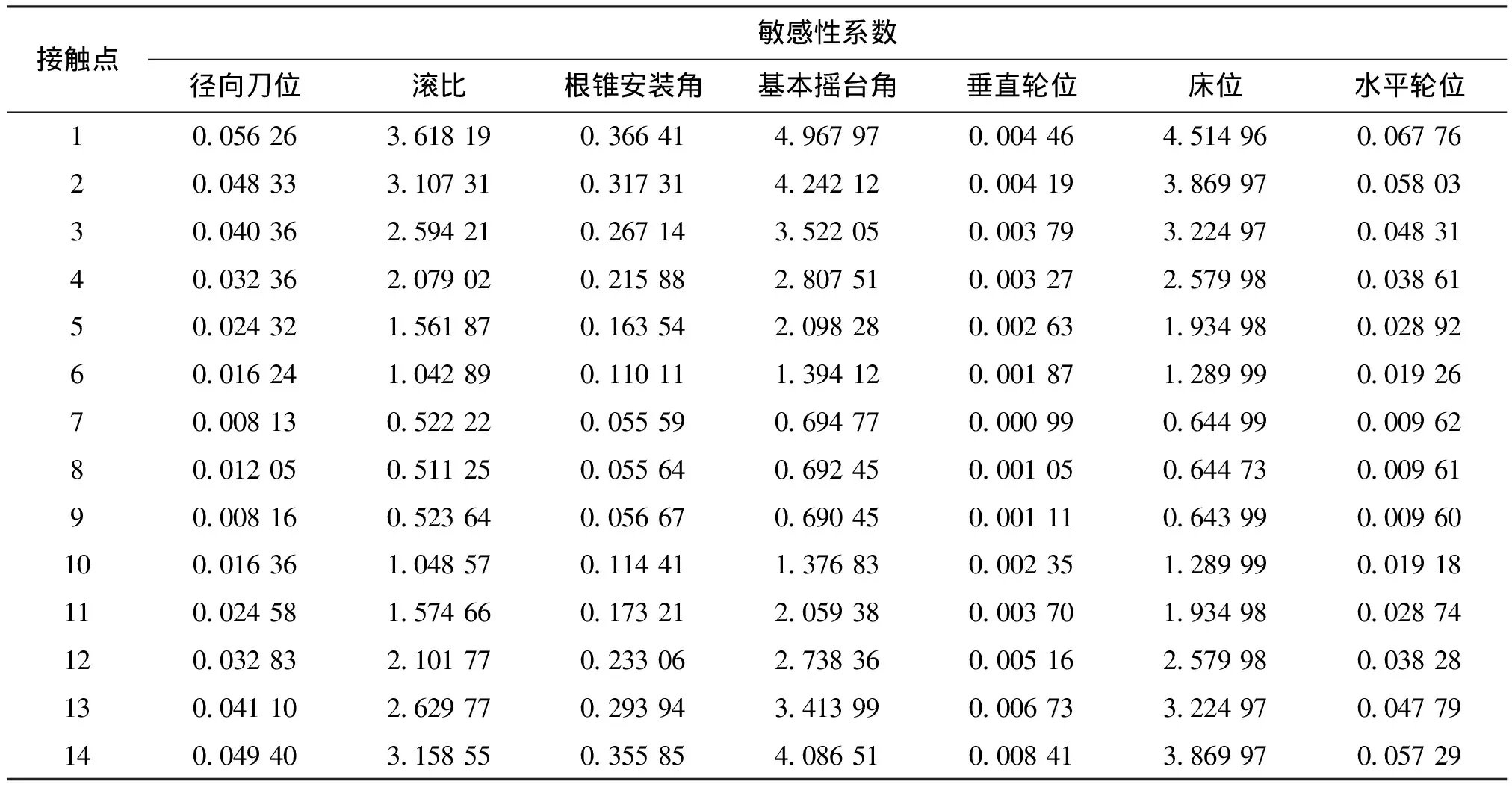
表3 接触点位置处各加工参数的敏感性系数

表4 基于6σ鲁棒性优化的精确加工参数和反调量
4.3 MOO方法求解结果评价
通过上文提出的求解算法可进行物理性能和几何性能评价项的评价。图5a给出了参数反调和优化参数二次反调后的齿面ease-off,即目标齿面与基本齿面之间的距离偏差,设为H,参数反调后的H最大值为55.644 μm,最小值为-47.69 μm;优化参数反调后的H最大值为53.465 μm,最小值为-45.83 μm。优化参数二次反调后的齿面接触点位置的残余ease-off(hRMSE)如图5b所示,其中,最大残余ease-off为2.178 μm,最小值为-1.870 μm。此目标齿面能反映出足够的齿面精度,因为比铣削加工精度更高的磨削加工的精度量级一般为50 μm[21]。与上文客户所给的目标值对比可知,参数反调和优化参数反调都能达到提高齿面精度的作用且都满足设计预设的目标值;由于优化参数二次反调在普通参数反调的基础上优先考虑敏感性系数较大的加工参数进行反调,避免了较多个加工参数之间的耦合作用影响,优化参数反调的效果比参数反调的效果好。总体来说,通过再次的优化参数反调修正,残余误差精度有了很好的提高。
图6给出了MOO方法求解后的物理性能评价项。如图6a所示,齿面接触区域位于一个合理范围内,且最大接触压力CPMAX达到了978.25 MPa,主要分布区域呈长条形椭圆分布,且沿齿宽方向呈现对角倾斜状态,表明了齿面具有足够的接触强度。在图6b中,最大载荷传动误差LTEMAX为44.685 μrad,且整个传动误差变化平稳,传动噪声和振动性能好。如图6c所示,重合度CR为1.63。另外,机械效率η可以通过计算公式求得为95.32%。通过与上文中提出的所要求的目标数值相比较,都达到了满意的设计要求[22]。
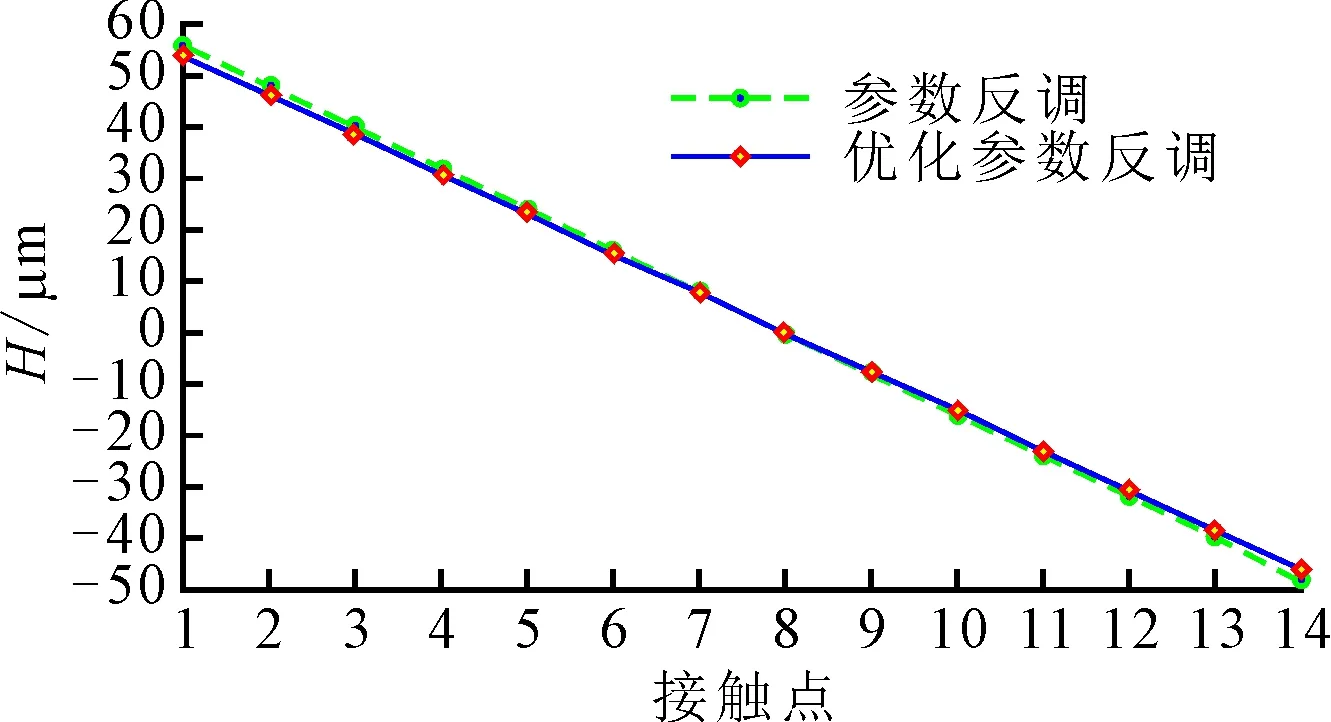
(a)齿面ease-off

(b)求解的残余ease-off图5 MOO方法求解后的几何性能评价项
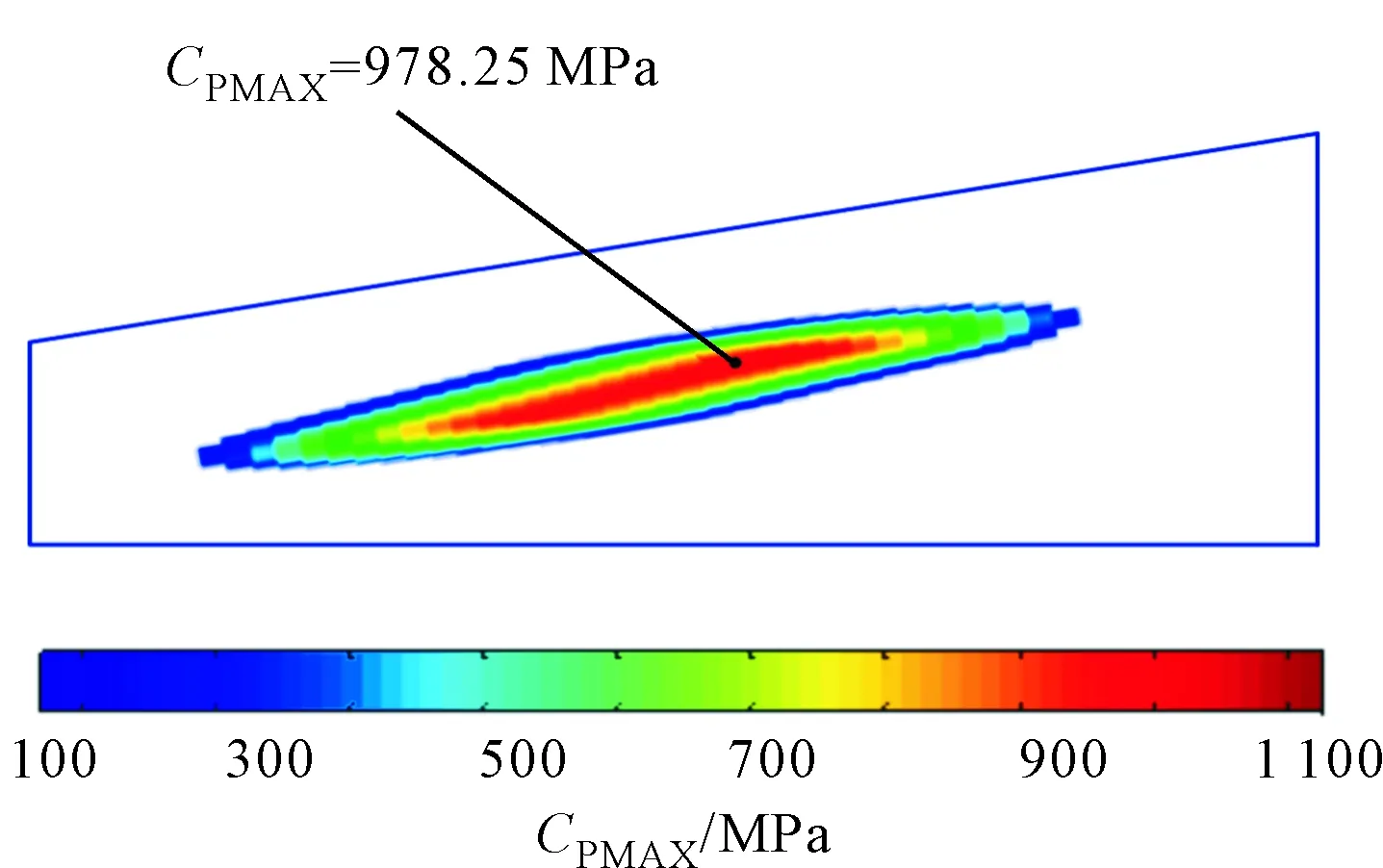
(a)CPMAX
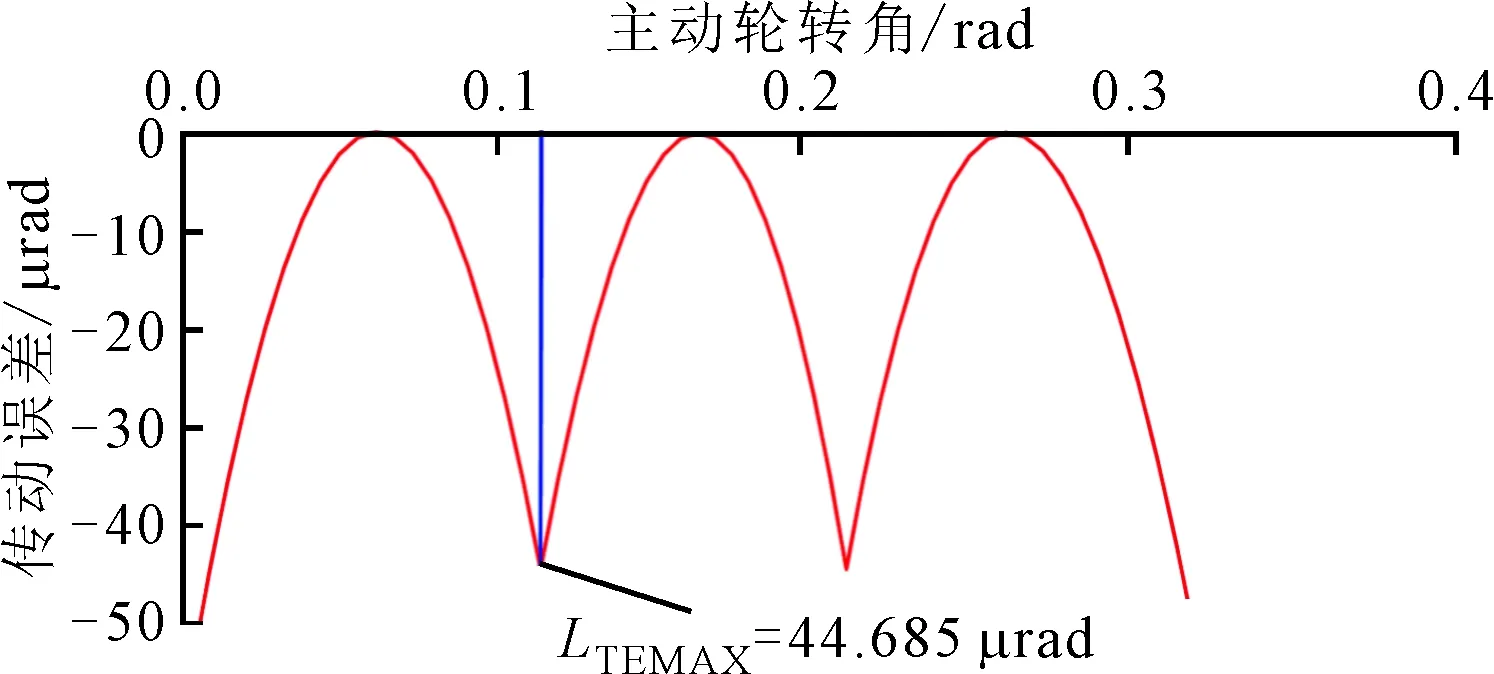
(b)LTEMAX
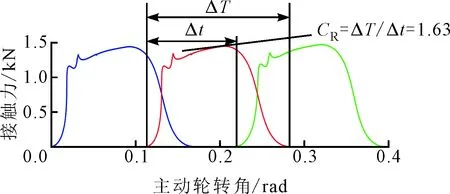
(c)CR图6 MOO方法求解后的物理性能评价项
5 结 论
(1)基于现有6σ设计流程,提出了一种改进的DMAIC框架,即定义-测量-分析-改进-控制框架;基于改进的参数驱动关系,构建齿面评价项的多目标函数,完成产品性能的直接参数驱动决策与优化。
(2)采用模糊QFD的方法,将客户对齿轮产品的需求转化为相应的产品质量信息,建立基本的MOO模型,引入6σ鲁棒性优化设计方法,得到考虑形性协同的鲁棒性优化的MOO模型,采用提出的求解算法,计算加工参数反调量和优化加工参数二次反调量,根据计算的反调量,通过LTCA方法求解得到齿面加载接触性能。
(3)以一对航空用螺旋锥齿轮为例,利用所提方法计算得到MOO加工参数反调量,根据反调量获得最终的齿面评价项LTEMAX、CPMAX、CR、hRMSE等,与客户提出的设计要求对比验证,较好地满足了设计要求,证明了设计方法的正确性,可为将来的螺旋锥齿轮形性协同制造及智能制造提供技术支撑。

