压力容器服役质量指标体系构建及评价方法研究

姜洪权,周涛,高建民,夏锋社,王荣喜,张晓明,刘东程

(1.西安交通大学机械制造系统工程国家重点实验室,710049,西安;2.陕西省特种设备检验检测研究院,710048,西安)

压力容器是一种易发生爆炸、泄漏,造成重大财产损失甚至人员伤亡的特种设备,广泛用于化工、炼油、能源动力等领域[1]。虽然我国自20世纪80年代后逐步建立了压力容器的安全管理体系[2],安全状况得到了极大改善,但仍然无法准确把握压力容器在服役中的质量状态,安全事故时有发生。因此,研究压力容器在服役过程中质量状态评价技术,对于保证企业的稳定生产运行具有重要的意义。

服役过程是压力容器全生命周期中重要组成部分,服役过程中的安全可靠性评价研究是热点问题。在评估压力容器安全状况等级方面,我国现行的《固定式压力容器安全技术监察规程》规定了压力容器在服役过程中进行强制定期检验,根据检验结果对其进行安全状况等级评定,并确定相应检验周期[3]。

文献[4]分析海洋平台压力容器事故的主要风险因素,用改进的层次分析法与灰色关联分析法组合对压力容器安全等级进行评估。20世纪90年代,美国石油协会(API)提出了基于RBI(Risk Based Inspection)风险等级分析技术,目前在国内得到了广泛关注和应用[5]。文献[6]基于RBI的理念,分析辨识制氢机组中的压力容器存在的危害因素,实现风险定性或定量评估,并提出降低风险的对策建议。

此外,在压力容器剩余寿命分析、裂纹与腐蚀缺陷机理方面也有相关研究[7]。文献[8]探讨了压力容器疲劳蠕变与动态应变时效之间的耦合作用,建立了一种半寿命平均位移速率寿命预测模型,对压力容器寿命进行预测。文献[9]以压力容器行业最为广泛使用的低合金钢16MnR材料为对象,研究压力容器服役过程中高温损伤对断裂韧性、低周疲劳寿命及应变疲劳裂纹扩展速率的影响。

现有关于压力容器评价方法及标准,主要是按照最弱环节原则进行评价,如RBI风险分析是针对具体危险源发生的概率和可能造成后果的严重程度、性质等进行定性或定量评价;还有一些方法偏重缺陷失效机理分析,着眼于功能完整性的评价。换言之,现有方法主要是以实现压力容器在使用过程中是否安全为主要目标进行分析,仅仅是压力容器服役过程质量评价的一个方面,涉及因素及方法不能满足当前服役质量管控的需要。因此,需要构建从用户角度、以服役过程质量管控为目的的压力容器服役质量评价体系与方法。

针对以上不足,本文提出了一种压力容器服役质量评价方法。首先进行了压力容器服役质量内涵分析,提出了压力容器服役质量的概念;其次构建了压力容器服役质量评价体系,实现从宏观层面对压力容器服役质量状态的有效刻画;最后提出了服役质量指数的概念。在属性数学评价模型的基础上引入了评语等级加权向量分析,并采用百分制的形式计算压力容器服役质量指数,使得评价的结果更能直观反映压力容器的服役质量状态。

1 压力容器服役质量指标体系

1.1 压力容器服役质量内涵

质量的概念与内涵随着社会生产力、科学技术等的进步而不断发展与变化,经历了符合性质量、适用性质量和广义质量(即大质量)3个阶段[10-11]。大质量从系统的角度,强调通过各子系统之间的协作与优化,提升系统整体有效性,追求整体质量的最优化[12-13]。国际标准化组织在ISO9000:2000质量管理标准中对质量进行了定义:一组固有特性满足要求的程度。质量的载体可以是产品(硬件、软件)、活动或过程、组织、体系、人以及他们的任意组合,从而使质量的内涵向广义化方向发展。由于压力容器服役质量是压力容器服役过程整体质量的全面反映,基于以上分析,本文从服役过程的角度对压力容器服役质量作如下界定。

压力容器服役质量是指保障服役过程平稳、高效运行,持续保持功能(如存储、反应、换热、分离等4大功能),以满足企业或客户要求的程度。内涵包括如下内容。

内涵1:具有运行过程质量、维护改造质量及管理过程质量3者的综合质量内涵。

内涵2:具有良好的平稳性和高效性的质量属性。平稳性是指运行过程能安全稳定运行,能够持续不断地提供符合企业满意的服务;高效性指各种资源得到充分利用,尽量减少容器运行过程中的能源浪费。

内涵3:具有符合顾客使用需求的质量属性。对压力容器而言主要是存储、反应、换热、分离功能满足客户要求程度。

内涵4:具有静态和动态的质量属性。不仅包括当前的运行情况,而且涵盖了未来发展的趋势,随着时间的变化服役质量也会发生变化。

1.2 压力容器服役质量评价指标体系

在上述服役过程分析基础上,本文提出了如图1所示的压力容器服役质量评价因素体系。其核心思想是,依据服役过程中的功能划分,将压力容器服役中的工作运行状态、设备整体结构、安全管理、人员素质因素,与压力容器服役中的使用、维修、改造、检验等过程进行融合,进而构建压力容器服役质量评价指标体系。

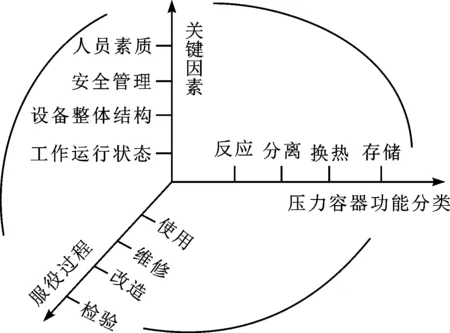
图1 压力容器服役过程因素体系

本文提出的压力容器服役质量评价指标体系如图2所示。其中,评价体系的目标层代表压力容器服役质量状态,第一级评估指标包括工作运行状态、设备整体结构等共计4项;第二级评估指标包括功能实现性、运行状态的可测性等共计15项。

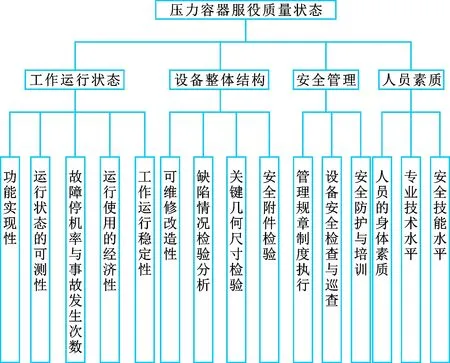
图2 压力容器服役质量评估指标体系

2 压力容器的服役质量评价技术

2.1 服役质量指标数据的获取方式

指标值的获取方式是在服役质量评估有效性、实时性的基础上,利用不同的数据及分析方法进行确定。限于篇幅及本文关注重点,在此仅对图2指标值获取方式及技术路线给出概要描述。如表1所示,一般可以通过3种方式获取相应的指标数据。其中,专家检查打分主要是依据相关要求,对难以量化分析指标值进行计算;历史数据分析主要是通过指标涉及的相关历史数据信息,通过制定特定的计算方法进行指标值确定;现场检测及数据分析主要是依据实际检测数据,结合相关要求及目标制定明确的分析方法,实现指标值计算。

2.2 压力容器服役质量指数概念及计算

在建立压力容器服役质量指标体系及获得指标数据之后,一般可用模糊综合评价[14-15]和属性数学评价[16]等方法进行评价。现有方法还存在一些不足,如在模糊综合评价方法中,隶属度函数确定的主观性太强,评价结果往往丢失很多信息;基于属性数学的评价方法可以得到客观的隶属度向量,但结果不够直观。因此,本文提出了压力服役质量指数的概念,并结合属性数学评价理论,以服役质量指数为最终结果实现综合评价。

压力容器服役质量指数是指:在各个影响因素作用下,压力容器保持运行平稳、高效,持续保持功能的能力,以及满足企业或客户要求的程度。计算公式如下

Q=AS

(1)

式中:Q为服役质量指数;A为压力容器的服役质量的隶属度向量;S为评语等级向量。显然,Q是一个动态指数,可以综合反映压力容器在不同情况下的服役质量状态。

属性数学理论广泛应用于解决综合评价与模式识别问题,数学描述如下:对Z中元素的某种评价称为评价空间F,把评语集V={C1,C2,…,Ck}称为对评价空间的分割,其中Ck称为一个属性集,j个指标的指标值t具有级别Ck用属性测度函数μjk(t)来表示。因此,所提出的基于属性数学理论的服役质量指数计算主要包括以下步骤。

(1)建立判断矩阵,确定指标的权重。建立判断矩阵An×n,以矩阵的形式来表达每一层次中各要素相对上下层要素的重要度。采用1～5标度[4]表示指标之间的重要程度,通过指标两两比较得到指标的判断矩阵。同时,利用方根法通过求取An×n的最大特征根计算各指标的权重,具体子步骤如下。

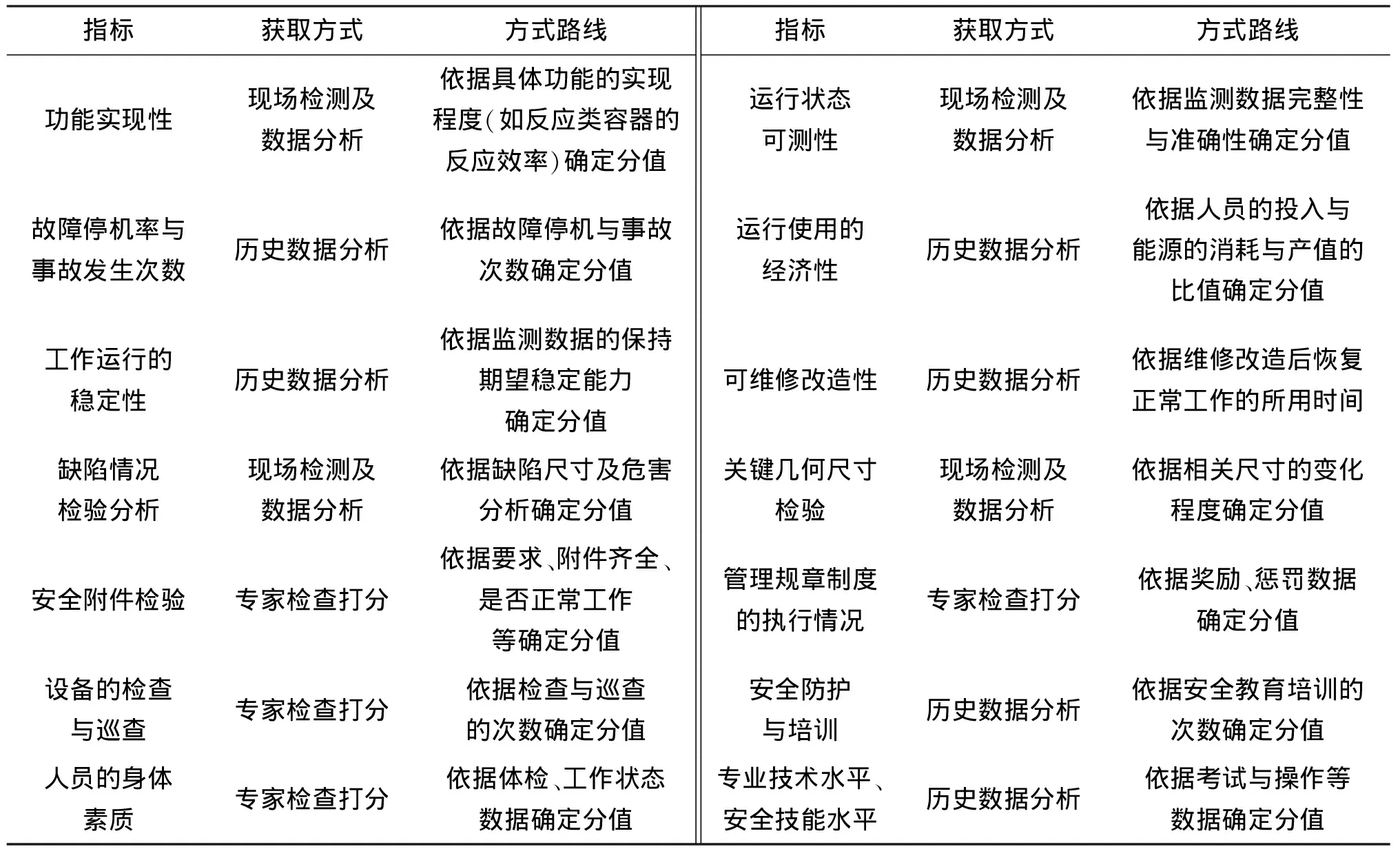
表1 指标数据及其获取方式

(Ⅰ)计算每一行各个元素的乘积Mk,即

(2)

(Ⅱ)计算Mk的n次方根

(3)

(Ⅲ)归一化处理得到指标权重

(4)

(Ⅳ)求取最大特征根

(5)

(Ⅴ)一致性检验,通过随机一致性指标CR进行一致性检验,公式如下

(6)

(7)

式中:CR为随机一致性指标,一般CR≤0.1可认为判断矩阵一致性满足要求,如果不满足则应修改判断矩阵,直到满足一致性为止[17-18]。

(2)确定评语等级。就是确定指标属于各个评价等级的程度,可将评语等级分为4个,即评语集V={C1,C2,…,Ck}。

(3)确定评语等级向量。为了使评价结果容易区分,本文对传统属性数学评价模型进行改进,即引入了百分值的评语等级向量S={A,B,C,D}。

(4)求取最底层指标的隶属度。根据实际情况的要求,将评价等级分为C1,C2,…,Ck,如表2所示,am(k-1)、amk分别是指标值等级划分的上、下限。

表2 评价指标等级的划分

假设第j个指标的值为t,需要由表2来求取指标属性测度函数μjc(t),在表2中,假定满足aj0

(8)

djc=min(|bjc-ajc|,|bj(c+1)-ajc|)

(9)

式中:c=1,2,…,k;j=1,2,…,m。

指标的属性测度函数μjc(t)如下

(10)

通过上述步骤可以计算出一级指标对应的二级指标的隶属度矩阵,利用二级指标的权重乘以二级指标的隶属度矩阵得到每个一级指标的隶属度向量Bi,由Bi构成一级指标的隶属度矩阵B

Bi=Wiui,i=1,2,3,4

(11)

式中:Wi表示对应的二级指标权重;ui表示对应二级隶属度矩阵。

通过各个一级指标的权重与隶属度矩阵B的乘积,可得到压力容器服役质量的隶属度向量A

A=WB

(12)

式中:W表示一级指标的权重;B表示一级指标隶属度矩阵。

(5)服役质量指数计算。对于压力容器服役质量评价指标体系是多层次指标体系,将服役质量状态的隶属度向量乘以评语等级向量,即可到服役质量指数,见式(1)。

3 实例分析

为验证本文方法的有效性,以某企业的压力容器服役过程中的一次运行数据为基础,建立服役质量评价体系,相关指标数据如表3所示。

表3 某企业压力容器的指标数据

由于篇幅的限制,图2中各级指标之间相对于上一级指标的判断矩阵与各个指标的评语等级划分没有列出,依据本文第2节所述方法进行服役质量指数计算及评价,主要步骤与过程如下。

(1)利用式(2)～(4),获得判断矩阵计算各级指标的权重,一级指标权重W=(0.077 8,0.124 8,0.491 8,0.305 6);二级指标的权重W1=(0.163 4,0.297 0,0.539 6);W2=(0.172 4,0.315 4,0.512 2);W3=(0.280 1,0.135 6,0.469 7,0.114 3);W4=(0.203,0.07,0.441,0.099 3,0.183 6)。

(2)根据式(8)～(10),可以得到各级指标的隶属度向量,以及人员因素、安全管理、设备整体结构、工作运行状态指标的隶属度矩阵B1、B2、B3、B4分别为

B1、B2、B3、B4每一行表示该一级指标下的二级指标的隶属度向量。利用二级指标的权重乘以二级指标的隶属度矩阵,得到一级指标的隶属度向量

Bi=Wiui,i=1,2,3,4

一级指标的隶属度矩阵B由Bi组成

B的每一行表示该一级指标的隶属度向量。

(3)利用式(12),可得到压力容器服役质量的隶属度向量

A=WB

即得到压力容器服役质量隶属度A=(0.508 7,0.464 2,0.027 1,0)。

(4)本文设置的评语等级向量S={95,82.5,67.5,52.5},联合式(1),可求得压力容器的服役质量指数Q=88.45。其实际指导意义为:由于Q采用百分制,因此可以定量化表示当前服役质量状态及未来趋势分析;同时,依据评语等级S可知,95>Q>82.5,即表示当前服役质量处于设置的第一等级与第二等级之间,满足宏观定性评价与管理需求。

综上所述,通过本文所提方法可以实现服役质量定量化的评价,并得到压力容器服役质量指数,结合实际评价需求,可直观地、实时地反映压力容器服役质量状态。

4 结 论

本文在分析压力容器服役过程特点及现代广义质量的基础上,提出了压力容器服役质量的概念及其内涵。结合压力容器在服役过程的特点,建立了包含人、设备、管理等因素的面向压力容器服役过程的质量评价体系,以及基于服役质量指数计算为核心的压力容器服役质量定量化评价方法。通过某企业压力容器服役过程的数据进行了实例验证,证明本文方法的有效性,为以后压力容器的对比分析和趋势预测分析提供了技术支持。

未来工作将围绕评价过程中数据获取标准流程、各个指标数据统一规范的计算方法进行研究,为推广应用、形成行业规范奠定基础。