碳纤维层合板Lamb波损伤检测的加权块稀疏成像法

徐冠基,许才彬,杨志勃,陈雪峰

(1.中车青岛四方机车车辆股份有限公司,266000,山东青岛;2.西安交通大学机械制造系统工程国家重点实验室,710049,西安)

近年来,碳纤维增强复合材料(CFRP)在轨道车辆前罩、车身、转向架等结构中得到越来越广泛的应用,以适应轨道交通车辆结构轻量化的要求[1-3]。由于CFRP在制造及服役过程中不可避免地出现分层、夹杂、裂纹等损伤[4],轻则导致结构失效,重则导致重大财产损失和人员伤亡。结构健康监测能够及早发现结构损伤,可以做到视情维修,从而提高结构的安全性,降低结构的维护成本,延长服役寿命[5]。

Lamb波即薄板中的超声导波,具有传播能量衰减小、对结构表面及内部损伤均敏感等特点,被认为是最具潜力的无损检测工具之一,在板状复合材料结构的损伤检测及结构健康监测中得到了越来越广泛的关注[6-7]。基于超声导波的损伤检测系统是一种主动式的结构健康监测系统,包含信号激励与采集模块。被测结构中若存在缺陷,会引起超声导波的散射,相当于一个次波源,从而散射信号会被预先布置的传感器阵列所采集。根据对所采集的响应信号在时域、频域、时频域、波数域等域中进行处理,从而实现对被测结构健康状况的感知与诊断。

Lamb波损伤成像就是对所采集的Lamb波响应信号进行处理,并最终得到与被测结构几何位置相关联的、反映损伤特征的图像。国内外众多学者研究与建立了多种Lamb波损伤成像算法。Wang等根据Lamb波传播的群速度信息,将各路响应信号进行延迟并叠加,以信号的幅值作为成像时的损伤指标,提出了Lamb波损伤成像的延迟叠加(DAS)法[8]。Hall等在DAS方法的基础上,通过最小化方差响应,引入自适应权重因子,提出了最小化方差无失真响应成像法,比DAS方法提升了成像质量[9-10]。Zhao等提出了一种概率重构成像方法[11],不依赖损伤波包的飞行时间信息,而是根据每对传感器位置信息对结构不同区域预先分配不同的权重,用测量信号与基准信号间的信号差异系数做损伤指标,但该方法需要构建密集的传感器网络以覆盖待测区域,对稀疏阵列传感器网络并不适用,且损伤定位精度不高。

近年来,稀疏表示作为数学与信号处理领域快速发展的方向之一,在超声导波信号处理方面也受到了研究者的极大关注。Xu等通过对频散导波在频散字典下稀疏分解并在非频散字典下重构,实现了多模态导波的频散补偿[12]。Harly等基于导波频率和波数关系的稀疏先验,在随机测点条件下实现了导波多模态频散曲线的恢复[13-14]。Mesnil等实现了稀疏测点下的全波场数据恢复[15]。Levine等通过将Lamb波损伤定位问题转化为稀疏重构问题,提出了稀疏损伤成像法[16-17],该方法具有定位精度高的优点,但同时因原子匹配问题而会在成像边界处引入伪点噪声。

针对现有成像方法存在的精度不高、伪点干扰问题,本文通过引入稀疏表示理论,将Lamb波损伤成像问题转化为加权块稀疏重构问题。基于Lamb波线性传播模型,得到激励源—潜在损伤点—接收源路径下的损伤散射信号,并以此为原子建立过完备字典库。将从结构中获取的损伤散射信号在所建立的字典库下进行加权稀疏分解,建立l1最小化的凸优化模型。最后采用谱梯度投影算法进行求解,得到稀疏重构系数并转化为对应成像点处的像素值,实现Lamb波损伤成像。CFRP层合板模拟损伤实验表明,所提方法能够实现高精度损伤成像,并能有效抑制伪点噪声。

1 Lamb波加权块稀疏成像算法

1.1 Lamb波线性传播模型

单层CFRP板属于力学性能各项异性材料,但由于在实际应用中,往往是以多层不同角度铺叠而成,即以层合板的形式存在。在铺层角度、层数较多的情况下,多层CFRP层合板中不同方向的力学性能差异缩小,可以将其看作是准各向同性材料[18]。将Lamb波激励源和接收源视为理想点源,不考虑导波模态转化效应,CFRP层合板中任意两点间的直达波响应可以表示为

(1)

式中:Y(ω)为响应信号的频域表达式;S(ω)为激励信号的频域表达式;m为Lamb波的第m个模态;km(ω)为Lamb波与模态m对应的波数;αm为与模态m对应的幅值响应;r为激励源至接收源间的距离。

在已知各模态的km(ω)时,由式(1)可以得到在任意激励下的导波响应,但准确的CFRP层合板的材料参数难以获取,导致km(ω)计算不准。为此,本文采用窄带信号激励,通过频率调谐技术[19]得到近似单一模态的Lamb波响应信号,在窄频带内将km(ω)近似作线性处理,则式(1)可以简化为

(2)

式中:cg(ωc)为中心频率ωc处的群速度。在CFRP层合板中,群速度可从信号求得[10]

(3)

如图1所示,假设在板中存在一处点状散射源(损伤),则损伤散射信号的传播路径为激励源—散射源—接收源,根据式(1)任意两点间的响应,单一模态损伤散射信号可以表示为

(4)

式中:Ysca(ω)为损伤散射信号的频域表示;α为激励源至散射源间的幅值响应;β为散射源至接收源间的幅值响应;r1为激励源至散射源间的距离;r2为散射源至接收源间的距离。

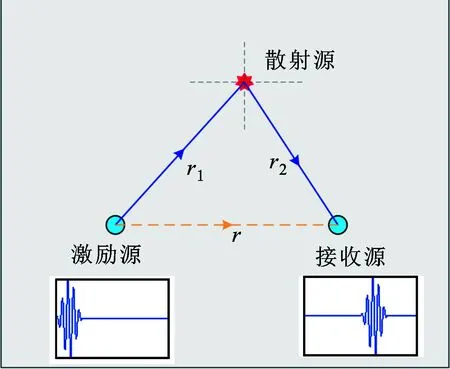
图1 两点间的Lamb波传播示意图

1.2 Lamb波成像模型的建立

为实现成像,将被测结构中待成像区域离散化为P个网格点,视每一网格点为一个独立的潜在损伤散射源。对于一个具有L个传感器对组成的传感网络而言,可以通过实验获取得到L组损伤散射信号。若在第p个网格点sp处存在一损伤散射源,则实验中第l条传感器组获取的损伤散射信号yl可以表示为

yl=al,pxl

(5)

式中:xl为散射因子,代表损伤可能性大小;al,p为损伤散射原子,公式如下

(6)

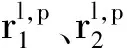
对于全部L组实验获取的损伤散射信号,可用损伤散射原子和散射因子表示为矩阵形式

(7)

由式(7)可见,对于L组损伤散射信号,通过损伤散射原子表示,将得到同样L个损伤散射因子。我们采用2范数‖x[p]‖2来表示第p个网格点存在损伤可能性(损伤指标)。

进一步考虑将式(7)应用于全部P个网格点,对于每个离散网格点,可分别构造出子原子库D[p],则实验获取的损伤散射信号可以通过这些原子库的合集表示

(8)

若从实验中获取的信号yl的长度是K,则信号y的维度为LK,字典D的维度为LK×KP,x的维度为KP×1。实际损伤成像中,字典中原子的个数KP往往远远大于信号的维度LK,即式(8)是一个高度欠定的方程。散射信号y可以从被测结构中获取,字典D可以根据上述的导波传播模型建立,只有x为待求量。当第p个网格点处存在损伤时,x[p]应具有非零值元素;反之,当第p个网格点处不存在损伤时,p应具有全零值元素,即向量x[p]中零值的出现与第p个网格点是否存在损伤相关联。

在实际被测结构中,损伤区域相对被测区域通常满足稀疏性假设,也就是向量x是组稀疏的。在向量是稀疏的条件下,x可以通过最小化l1范数求得

(9)

式中:wp为权重因子;σ∈[0,‖y‖2]为正则化系数,取值与噪声水平、实验信号、所构造字典的匹配度有关。在本文中,采用谱梯度投影算法[20]对式(9)进行求解,根据经验选择σ=0.5‖y‖2。

1.3 权重因子的确定

在式(9)中,权重因子wp若越大,则x[p]越趋向于稀疏(趋向于得到零值)。因此,在可能出现损伤的离散网格点sp处,应该赋予x[p]较小的权值;在其他位置则应赋予较大的权值。本文确定权重因子的原则为:若损伤散射信号与字典原子越相似,则赋予较小的权重;反义亦然。损伤散射信号与字典库中原子的相似程度用其相关系数表示

(10)

式中:Ap=[a1,p,a2,p,…,aL,p]T为由字典D中原子组成的第p个子向量;Cov、σ表示表示协方差、方差,分别由下式确定

(11)

(12)

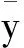
wp=101/ρp

(13)

在实际成像中,往往用信号的希尔伯特包络替代原始信号,以丢弃相位信息、提高成像稳定性,即

y←|y+jH(y)|;D←|D+jH(D)|

(14)

式中:H(·)表示希尔伯特变换。

2 实验验证

为了验证所提方法的有效性,对CFRP层合板进行了模拟损伤成像实验研究。实验平台如图2所示,主要包括EPA-104电压放大器、NI-1042Q机箱、NI PXI-5412任意信号发生器、NI PXI-5122信号采集仪及一套自编的基于LabVIEW的软件系统。被测试件为CFRP层合板,由16层单向铺层板复合而成。单层材料性能参数如表1所示,铺层角度为[0/45/-45/90]2s,几何尺寸为400 mm×400 mm×2 mm,如图3所示。在板中布置了由8个直径为8 mm、厚度为0.5 mm的PZT圆片组成的方形传感器阵列,实验中采用循环激励方式(8个PZT轮流作为激励源,其余作为接收源),采集Lamb波信号,则传感器对共有56对(激励i、接收j和激励j、接收i中,只取一个)。为模拟损伤,在板中分别胶接了2个质量块(直径为10 mm、高为10 mm的圆柱体铁块)作为散射源,模拟损伤对Lamb波的散射效应[21-22],分别进行了单损伤及双损伤模拟实验。

图2 Lamb波信号采集实验装置

E1/GPaE2/GPaE3/GPaG12/GPa94.17.767.762.53G13/GPaG23/GPaρ/kg·m3ν12ν13ν232.532.71 4420.310.310.43

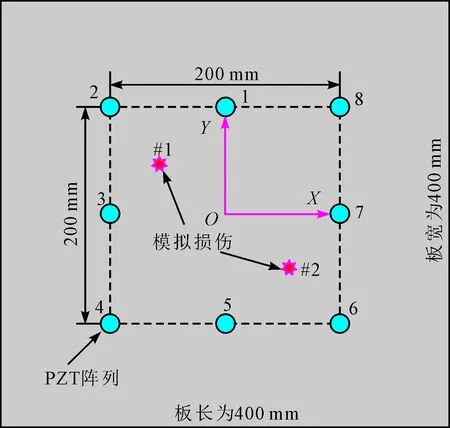
图3 CFRP中PZT阵列及模拟损伤布置

实验中,首先在无模拟损伤下测量得到56组信号,并以此作为基准信号。在引入模拟损伤后,采用同样参数测量得到56组信号,并将其分别与基准信号做差,得到损伤散射信号。实验中的激励信号根据频率调谐效应选择为一个5波峰、中心频率为80 kHz的Hanning窗调制的正弦信号,波形和频谱如图4所示。

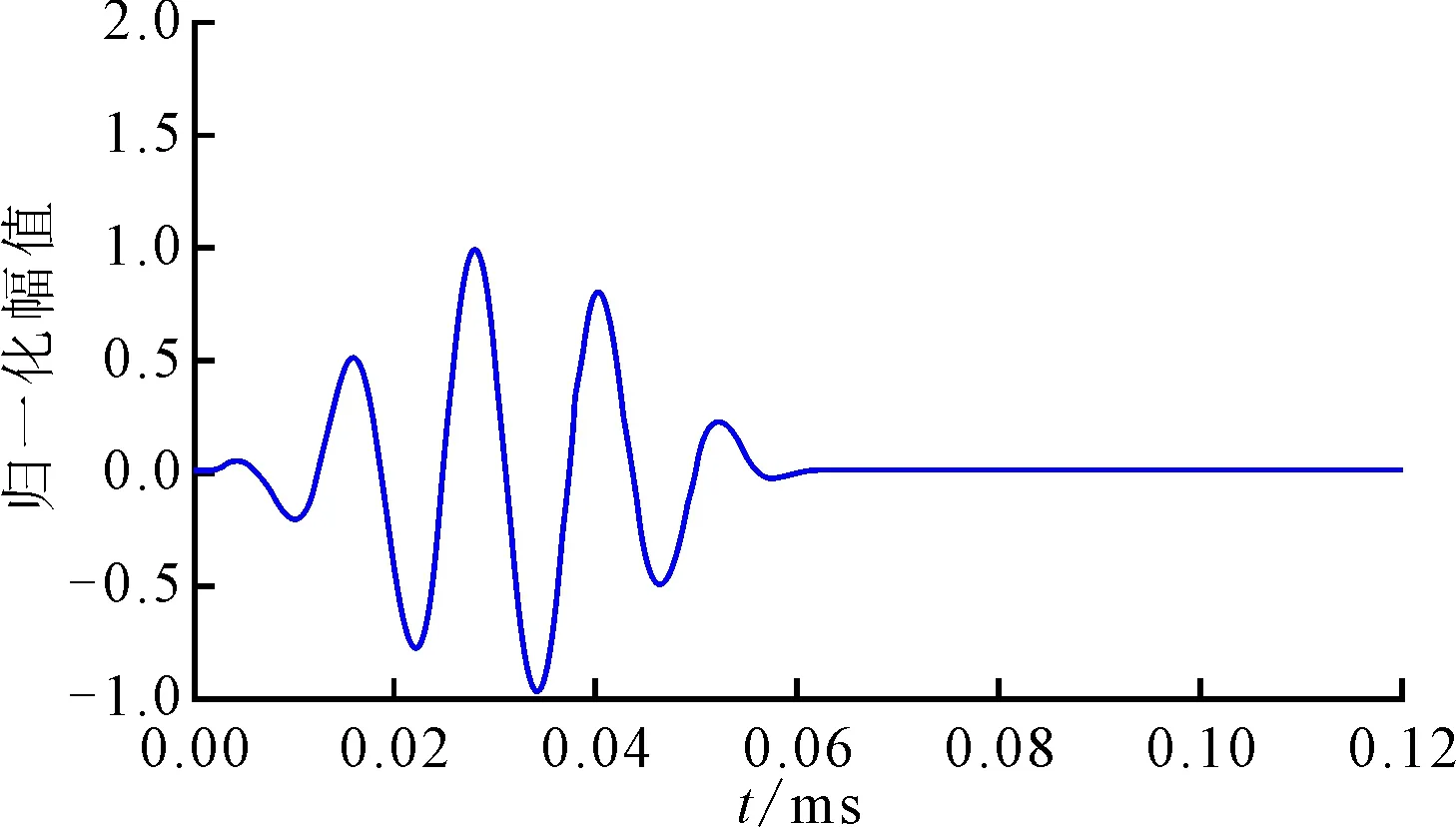
(a)时域波形

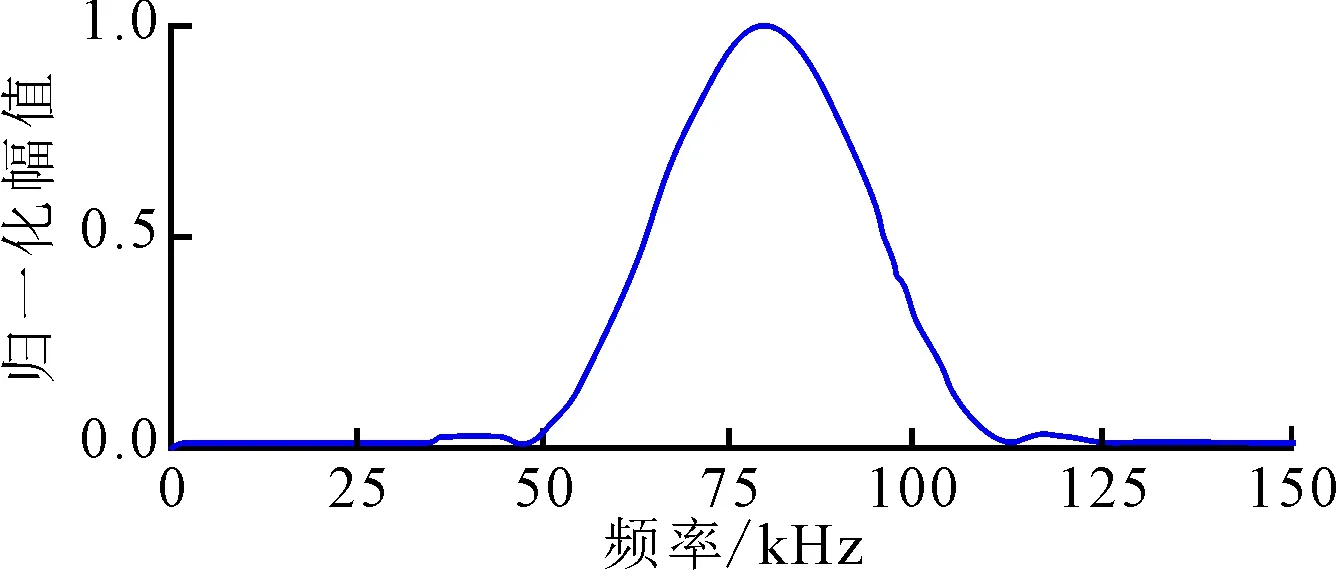
(b)频域波形图4 激励信号及其频谱

采集Lamb波响应信号时,采样频率设置为10 MHz,采样时长为1 ms。在成像时,为减少数据长度及运算量,以2 MHz进行降采样。在如4所示的激励信号下,试件中Lamb波响应信号主要以A0模态为主。在用式(3)计算群速度时,积分区间选择为激励信号的有效时域长度,即0～62.5 μs,群速度的计算结果为1 430 m/s。成像时,坐标原点选定在板的中心处,成像区域选择为整块CFRP板,离散网格为2 mm×2 mm。在损伤成像结果中,所有结果均用最大像素值归一化,并在20 dB范围内显示,该过程可用下式表示

(15)

式中:Ii为成像时第i个网格的像素值;x为计算得到的散射因子序列;‖·‖∞为无穷范数(等于序列中绝对值的最大值)。

单损伤的成像结果如图5所示,从结果中可见,DAS方法所得结果存在较大的背景噪声,且各网格点像素的动态范围(最大、最小像素值之差)较小。加权块稀疏成像法所得结果中,所得光斑尺寸较小,说明其损伤成像分辨率较高。以结果中最大像素值对应的位置作为损伤定位的位置,其结果如表2所示,可见两种方法在本案例中的定位准确度一致。

(a)DAS方法

(b)本文方法图5 单损伤的成像结果

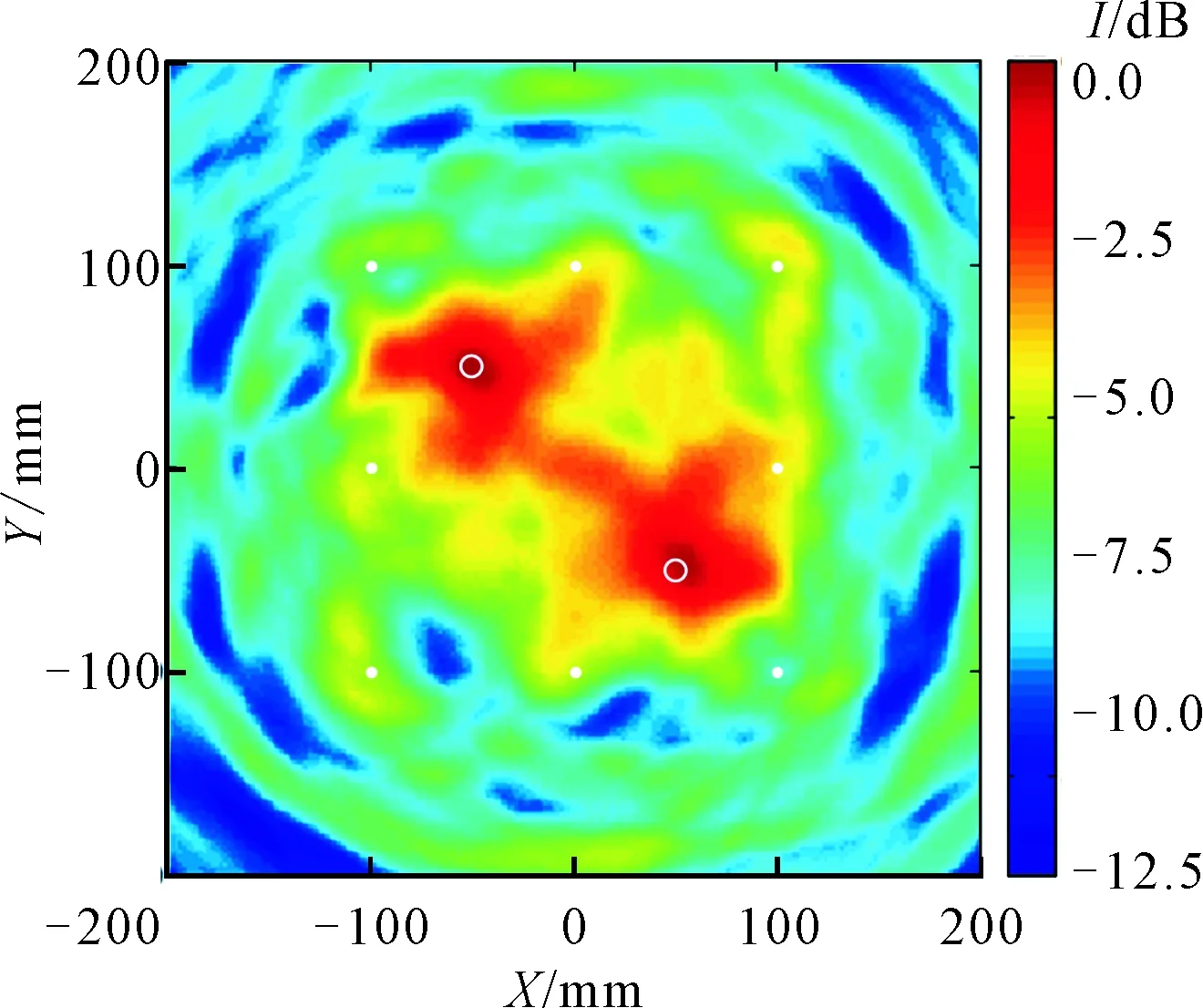
(a)DAS方法

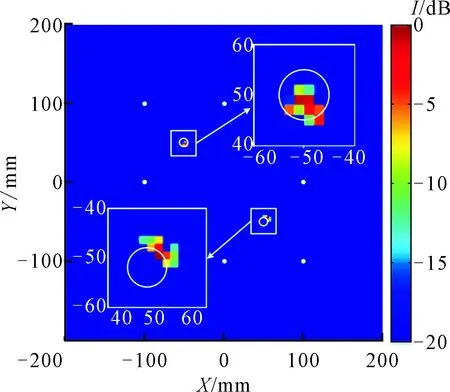
(b)本文方法图6 双损伤的成像结果

双损伤的成像结果如图6所示。与图5相类似,本文方法相比传统DAS方法,所得结果具有更小的背景噪声干扰、更小光斑尺寸。分别以真实损伤位置附近的像素极大值点作为损伤定位的位置,结果如表2所示。由表2可见,在(50,-50)位置处,本文方法得到了更小的定位误差。双损伤成像结果进一步验证了所提方法的有效性。

由于本文方法需要求解如式(9)所示的优化问题,计算复杂度远远大于DAS方法(DAS方法仅需对信号进行简单的延迟、叠加操作,不涉及计算量较大的优化问题)。为了对比两种成像算法的计算复杂度,在此采用简单的CPU运行时间作为计算复杂度的指标进行了对比,其结果如表2所示。所得CPU运行时间均为对应案例下的算法在Windows 7系统(Intel Core i3-4130 CPU,主频3.4 GHz,内存8 GB)中安装的MATLAB R2014a平台运行100次后取平均的结果。从表2可见,本文方法的CPU运行时间是DAS方法的10倍左右,尽管如此,本文方法也能在5～6 s时间内完成计算。

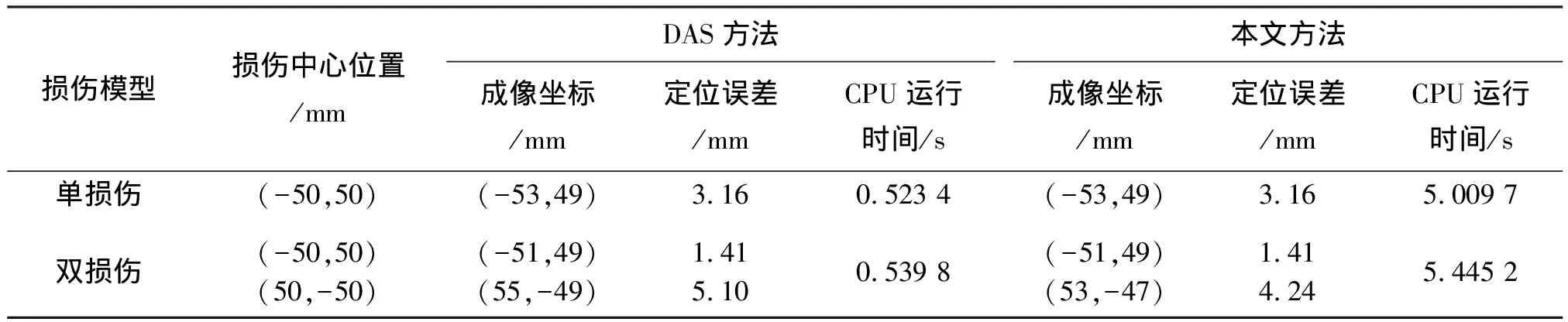
表2 两种方法损伤成像结果的比较

3 结 论

本文依据Lamb波线性传播模型,通过将被测结构离散化后的每一网格点视作潜在的损伤源,得到对应的激励源、散射源、接收源3者间的Lamb波损伤散射信号,以此信号作为原子,构建了块状过完备损伤散射字典库。将实际所测得的损伤散射信号在该原子库下进行稀疏表示,建立了l1范数最小化的加权块稀疏重构模型,将Lamb波损伤成像问题转化为加权块稀疏重构问题。通过CFRP层合板上的模拟损伤实验,并与传统DAS成像方法作了对比,可知本文方法能够得到背景噪声更低、光斑尺寸更小的成像结果,验证了所提出的加权块稀疏成像法在Lamb波损伤成像中的有效性,为板状CFRP层合板的损伤检测提供了另一种解决方案。同时也应该指出的是,本文方法需要求解l1范数最小化的凸优化问题,相比传统DAS方法需要更大的计算量。

因为本模型是一个线性模型,若能得到不同Lamb波模态的响应幅值之比,可拓展至多模态Lamb波损伤成像中,实现多模态Lamb波的损伤成像。