无人机编队协同追踪控制律和编队信息架构

张佳龙,闫建国,肖冰,吕茂隆

(1.西北工业大学自动化学院,710129,西安;2.空军工程大学装备管理与安全工程学院,710051,西安)

近年来,多无人机编队控制问题一直属于研究热点[1-2],主要包括航迹规划、任务分配、信息融合以及协同编队控制器设计。文献[2-5]中智能体上的测距传感器能够测量与其相邻智能体的相对距离,实现对无人机编队的控制。对于这种控制方法,智能体局部参考系的定位与全局坐标系是一致的,但是对于单积分、双积分以及多重积分器系统,其局部参考坐标系的定位与文献[6-8]不一致,因此这种基于距离控制的方法简单可控,但具有一定的局限性。在多无人机编队控制中[9-12],涉及协同编队飞行、避障、航迹规划、信息融合、最优感知以及信息构建等关键技术。针对上述学者研究中存在的不足,本文提出了分布式控制律的设计和扩展性信息构建两种研究方法,并对上述两种方法的收敛性进行了充分证明。

在无人机协同编队追踪问题中,多无人机仅利用局部信息以预定的空间角度绕运动障碍物在圆形轨道飞行。对于已知全局信息的目标,无人机编队以特定的队形分布在目标周围[13],以实现追踪的目的,但是局部信息一般很难获取,因此这种方法也有一定的不足。近年来,Frew和Lawrence提出了拉氏导引矢量场法来保持预定的追踪半径[14],但忽略了一个重要的时域分离问题,即无人机航向和追踪半径收敛,分析了任意两架无人机以不同的速度完成预定的空间角度,没有完整地证明在运动目标周围的无人机是否收敛。针对追踪问题,Kingston和Beard也采用了拉式导引矢量场方法,而且仅使用航向控制来获得期望的圆形轨道和空间位置[15],但忽略了在有限时间确保航向收敛。

基于以上研究的不足,本文将进一步研究拉式导引矢量场方法引导无人机在期望的圆形轨道飞行,通过解决时域分离问题证明该方法,同时提出一种航向收敛方法。本文主要创新点如下:①在无风且目标静止的情况下,所提出的导引势场方法能够使多无人机编队在运动目标周围渐进收敛至既定的圆形轨道;②在有风且目标运动的情形下,所提出的自适应估计方法能够使无人机实现以期望的圆形轨道和空间角度飞行,并应用图论建立多无人机编队模型以完成分布式控制器的设计;③所设计的速度控制器能够使不同无人机编队模型实现以期望的空间角度飞行。

1 建立数学模型

1.1 建立模型

单架固定翼无人机运动学模型如下[15]

(1)

式中:(x,y)为无人机惯性坐标系下的位置;ψ为航向角;μ1为空速指令;μ2为航向指令。假设在最大和最小空速约束下,有如下不等式

0<υmin≤μ1≤υmax

(2)

航向角速率峰值约束为

|μ2|≤ωmax

(3)

最大航向角速率约束等效于最小转弯半径约束,其中rmin=4μ1/ωmax。航向角和空速指令会导引无人机在目标周围的圆形轨道上,而且目标在圆心处处于静止状态。构建拉普拉斯函数,表达式如下

(4)

(5)

式中μ0表示无人机的速度。导引矢量场用极坐标表示为

(6)

式中θ表示无人机与期望轨迹的圆心连线与x轴正方向的夹角。

(7)

由LaSalle的不变性原理可知,无人机运动轨迹渐进收敛于期望的半径[14]。事实上,矢量场是近似解析方法。通过观察可知,运动学方程式(6)与θ无关,由此可得下式

(8)

方程式(8)的解为

(9)

式中r0=r(0),将其代入方程式(6)中,可得到关于时间的函数

(10)

式中θ0是极坐标下初始方位角。

在导引势场作用下,方程式(9)(10)包含全部的解析解,因此无人机的运动轨迹是已知的。通过方程式(5),可得沿着矢量场的航向角

(11)

对式(11)求导数,可得

(12)

根据方程式(11)可知,无人机运动轨迹将收敛于期望的圆形轨道,从而证明了初始航向与导引势场的方向是一致的。然而,在一般情况下无人机的初始航向与导引势场方向不一致,下面将给出一种无人机航向收敛的方法解决此问题,并证明此方法的有效性。

1.2 航向收敛证明

Frew和Lawrence提出了一种航向反馈方法获得快速收敛[14],然而缺少航向收敛和时间尺度分离的证明。其他研究方法则采用动态滑模控制器解决无人机航向收敛问题[16-18],这种不连续且已知外界因素的情况,则会导致执行机构发生振颤。

由于x=rcosθ和y=rsinθ,则角度φ定义为

(13)

同时,无人机动力学方程式(5)可改写为

-μ0[sinθcosφ-cosθsinφ]=-μ0sin(θ-φ)

(14)

根据方程式(11)和(14),可得角度之间的关系

ψd=θ-φ+π

(15)

假设无人机初始航向误差定义为

ψe=ψ-ψd

(16)

式中ψd为期望的航向角。假设航向角速率的输入u2定义为

(17)

对于式(17)中的反馈增益k>0,同时可以获得快速收敛反馈误差ψe(t)=ψe0e-kt,其中ψe0=ψe(0)。式(17)中的k控制航向误差收敛的速度,它的选取直接影响转弯速率。这就需要在反馈和前行反馈环节寻求一个恰当的平衡点。联立方程式(1)(16),无人机动力学表示为

(18)

由方程式(11)(18)可知,当存在期望的航向误差时,可获得期望的航向角速率

(19)

无人机初始航向所处象限的位置直接影响航向反馈的有界性和收敛性,如图1所示,曲线表示导引的轨迹,初始值设定为μ0=20 m/s,rd=300 m,x0=600 m,y0=600 m。期望的航向角与轨迹是相切的,一般情况下,实际初始航向将与导引矢量场方向不一致,而是指向4个象限之一的方向。

图1 无人机航向导引轨迹图

2 控制器设计

在追踪运动目标过程中,由于受到风场的影响,运动目标的前行速度和多无人机编队追踪的速度会发生变化,这种变化使无人机不能准确定位目标,从而不能达到追踪目标的目的,因此有必要考虑风场的扰动,本节设计了给定运动学约束的空速控制器解决此问题。

2.1 具有自适应风或运动目标估计量的可变空速控制器

无人机的运动学方程如式(1)所示,它表示相对于运动目标的数学模型,加入风影响后的模型为

(20)

式中:(Wx,Wy)表示恒定风速在x、y方向的分量;(VxT,VyT)表示目标在惯性系下恒定的运动速度在x、y方向的分量。风速和目标运动速度都会影响模型的动力学特性,将两者对无人机动力学模型的影响用一组变量表示为

(21)

式中:Tx和Ty分别是无人机在x、y方向的速度。假设上界可行性,T*满足下式

max(Tx,Ty)≤T*

(22)

式(22)指无人机在风速与运动速度耦合作用下能够稳定飞行的速度变化范围。考虑到以下控制器设计

(23)

(24)

空速的输入如下式

(25)

式(24)给定的航向角与已获得的航向角速率输入是有区别的。将方程式(20)(23)联立,可得

(26)

(27)

定义误差信号为

(28)

同时,响应误差动力学如下式

(29)

由式(29)可知,实际的轨迹和导引势场作用下的轨迹是重合的,它表明rp(0)=r(0)和θp(0)=θ(0),因此在初始时刻航向角收敛于在拉氏矢量场对应的角度,此时误差信号为0。

2.2 稳定性分析

为了确保风和运动目标的估计量在所给定T*的范围之内,定义新的变量如下式

(30)

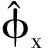
(31)

考虑拉普拉斯函数,如下式

(32)

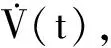
(33)

对于信号β和正常数kθ,可知

(34)

式中参数γ表示一种自适应学习速率,它可以控制如何快速适应方程式(33)。为了消除式(34)中信号的不确定性,定义β如下式

(35)

可得

(36)

(37)

(38)

因此,通过增大学习速率参数γ,运动目标导引轨迹的最大半径误差减小。通过调整控制器的参数能够实现无人机追踪目标的不确定性,同时解释运动学约束。

3 编队信息架构

无人机编队控制最基本的任务就是以最优的队形分布保持预设的编队形状。这一节主要研究无人机编队队形的信息构建,以满足最优的无人机编队。在组合方法理论[19-21]中,图论中的“刚性”是描述无人机编队之间信息构建以满足编队几何形状。基于图论建立3架对称结构无人机编队模型,如图2所示。

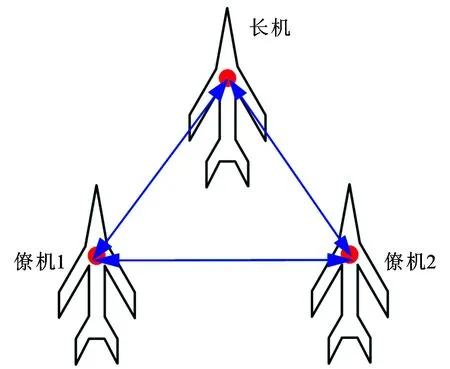
图2 3架无人机编队网络拓扑关系图

3.1 控制律设计

目标分为静止的和运动的,本小节主要研究无人机处于静止目标周围,通过设计无人机编队分布式控制律能够实现其期望的空间位置。

以3架无人机编队和一个目标为研究对象,以下给出第i架无人机在极坐标下的动力学模型为

(39)

设定第n架无人机有一个定常空速

μ1n=μ0

(40)

其余的n-1架无人机空速为

(41)

3.2 稳定性分析

定义空间角误差为δ(θi)=θi+1-θi-θd,对其进行求导,然后结合方程式(41)得到空间角误差动力学方程

(42)

为了验证无人机编队分布式控制器的稳定性，式(32)可进一步改写为

(43)

选择合适的λi,通过联立方程式(40)(43),可计算出函数V的导数

(44)

其中

tanh(δ(θi))=(tanh(δ(θ1)),…,tanh(δ(θn-1)))

(45)

式(43)可以简化为

(46)

矩阵C的正定形式为

C=

(47)

选取

(48)

∀i

(49)

可获得期望圆半径为

∀i

(50)

这样,可以实现空间角度控制。

4 仿真实验

仿真初值设置如下:μ0=20 m/s,rd=300 m,ΔVmax=5 m/s,x10=500 m,y10=500 m,ψ10=0,x20=-800 m,y20=-600 m,ψ20=π/2,x30=-500 m,y30=500 m,ψ30=π,x40=700 m,y40=-100 m,ψ10=-π/4。仿真曲线如图3～6所示。

图3 无人机编队相对静止目标的距离误差

图4 两架无人机在静止目标周围相对距离误差

图5 两架无人机在运动目标周围保持圆形轨道和空间距离的空速指令曲线

图6 两架无人机在运动目标周围的轨迹

图3采用3架无人机编队作为一个控制体,并给出了无人机编队相对静止目标的距离误差,随着时间的变化,曲线呈现一种快速下降后趋于水平的趋势。从图4可知,无人机编队由长机和两架僚机组成,它们以正三角形编队接近目标。在15 s之前,3架无人机以长机在前且前行速度均大于两僚机,它们之间的几何形状始终保持三角形,但非全等;在15 s之后,3架无人机处于以目标为圆心、以它们之间的相对距离为半径的球形表面上,同时它们以相同的姿态和位置渐进靠近目标。这是由于在接近目标之前,无人机以最快的速度和最优化的路径追踪目标点,当快接近目标时,以三角形编队协同追踪目标。

图4和图5均采用两架无人机作为控制体。图4给出了任意两架无人机相对距离误差随时间的变化,曲线呈现一种先迅速减小后缓慢增大、之后趋于水平的趋势。在多无人机近距编队追踪运动目标过程中,无人机翼尖因气流影响产生涡旋效应使得无人机前行阻力减小,从而使无人机前行速度增大。6.5 s时涡旋效应最强烈,此时无人机编队之间会产生一种相互排斥的作用(等效于两架无人机带同种电荷,产生排斥作用)。7 s后在引导矢量场作用下,两架无人机的相对距离误差保持恒定不变,呈三角形编队追踪目标。

图5给出了无人机编队在运动目标周围的圆形轨道飞行对应的空速控制指令曲线。两架无人机呈现一种协同飞行的趋势,但是存在一定的迟滞现象。在设计协同追踪控制器过程中,每架无人机安装控制指令传感器,当无人机编队飞行过程中,存在接收信息有偏差的现象。

图6给出了任意两架无人机在运动目标周围渐进收敛的曲线图。在无人机快速追踪运动目标过程中,为了保证编队的队形无人机会随时改变航向;在引导矢量场作用下,两架无人机按照设计的控制律,渐进收敛在期望的圆形轨道上。

5 结 论

针对无人机协同追踪目标问题,设计了一种控制律并证明了其稳定性,同时无人机能够以最优轨迹追踪运动目标。针对单架无人机的航迹规划,提出一种航向角收敛方法,解决之前忽略的时域分离问题。在多无人机编队协同追踪目标过程中,可变空速控制器能实现两架无人机以期望的圆形轨道飞行。此外,采用图论建立无人机编队之间信息交互的模型,有利于编队的全局控制,从而实现全局渐进稳定。

本文研究仅限于智能控制方面,还有较多潜在的方向需要研究:①随着编队中无人机的数量增加,无人机相互之间的动力学耦合作用比较复杂;②自适应控制技术可以扩展到更一般的运动目标,并且需要在实际工程中进行验证;③分布式编队控制与图论结合起来,这将有助于对一般非对称编队队形进行控制研究。针对多约束下的无人机编队信息构建,分布式控制具有较好的容错性和适应性,更有利于编队结构的实现和维护。