因势利导，让习题促进深度学习

□ 贺雪峰

在数学教学中，习题的设计往往举足轻重，不仅是教师教学力的体现，也是教师对教学内容理解力的反映。习题也是引起学生学习兴趣，提升数学思维品质的重要资源。然而在教学中，题海高耗、同题低效的现象却时刻影响着学生的学习。如何设计精到的习题，让学生愿学、乐思，在师生的互动间使学习深度发生？笔者在教学中基于学情，因势利导，用好、用足、用透习题，使课堂教学显得灵动而高效。

一、因势而谋，使学前经验得畅通

随着学生年级的升高，其生活经验和积累的数学知识对于学习的影响越来越凸显，教学时我们不能对其先前的经验置若罔闻，而是要充分利用。课前的习题设计为整节课奠基定调，也是引导学生沉浸于课堂的关键。如四边形的认识，对于三年级的学生来说，并不陌生，课一开始，教师就直接出示一些四边形让学生进行判断：把你认为是四边形的图形圈出来。教师随即对学生生成的情况加以分析，从而促使学生进一步认识四边形。

图1

图2

生：圈出来的这些图形都有四条边，四个角。生：图1中第一行第四个不是四边形。角的顶点是尖尖的，它是圆圆的。

生：图2中的正方形和长方形也是四边形。它们是特殊的四边形。

师：那我们怎么判别四边形呢？你能说说什么是四边形吗？

在“基于认知”中有序地呈现学生认知缺失的两种极端：与特殊四边形有异的一般四边形未圈，有专属名字的特殊四边形未圈。让学生在生生互动中对四边形的特征深度认知：“只要具有四条边、四个角的图形都是四边形。”如果再让学生根据认知，在方格纸中画一个不同的四边形，学生画了一个“凹四边形”，也是对前面特征深度认知的一个另类诠释，当然，这也是其他学生的认知盲区。学前的经验有很多是不完善的，但正是这样真实的认识，使学生对概念的认知在问题面前暴露出来，教师可以大胆利用学生这种错误“将错就错”，以此为基点，畅通经验与认知的渠道，引发教学的生长。

二、应势而动，在思辨差异中联通

学生对于数学的理解力和接受性因人而异，当课堂上师生共同参与数学活动后，其成效也是参差不齐，但正是这些不同，引发了我们对于真实课堂的认识，亦是深入学习的切入口。

（一）加强变式，促思考

在课后巩固类习题设计时，题组型的练习更能体现思考的有效性。让学生面对相似的练习，不敢掉以轻心，串联式的问题，让学生反复琢磨，不断深入思索，逐渐构建起知识链。如有教师在设计《梯形面积》练习时，出示如下题目（如图3）。学生运用已有的知识马上发现这三个梯形的高相等，它们上下底的和也相等，因此推理出这三个梯形的面积也应该相等。

图3

教师见势追问：你还能画出跟这些图形面积相等的梯形吗？

教师出示部分学生作品（略）。

待学生完成后，师追问：刚才作图时有什么万能的方法吗？

生：高一定，只要上底和下底的和是10厘米就可以了。

生：高缩小到一半，上底和下底的和就要扩大到2倍。不过这样画起来更麻烦。

出示几何画板，让学生操作变动，感悟面积的不变性和梯形形状的改变。当一个梯形的上底缩短5cm，下底伸长5cm，变化后的梯形面积是多少？学生的感知一目了然。

随即出示，当上、下底相等，上底为零时的两种特殊情况。

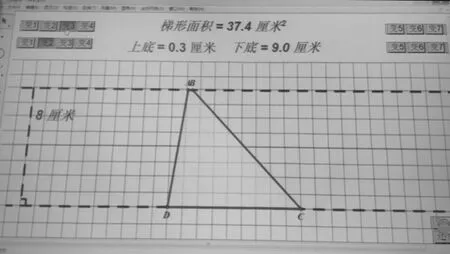
师：现在是什么图形？这时的面积有没有变化？

沟通梯形面积计算与三角形、平行四边形和长方形之间的关系，拓宽了学生的视野，使学生明白梯形面积计算公式是一个“万能公式”。学生从中感悟到，其实数学中许多图形之间存在着神奇的联系，只要我们用心观察、思考和发现，就能找到更多的秘密。

（二）引发冲突，助思辨

课堂应该多让学生生发意见相左的争辩，引发不同学生间的认知冲突，使“真理”越辩越明。教师在设计相关习题时，要给学生的思考留下空间，给思辨留有余地。教师可以利用作业中出错较多的习题，重点进行讨论，细化过程，强化方法。如判断：两个三角形等底等高，就一定能拼成一个平行四边形。面对这样的问题，总有同学会出现差错。如何厘清这个错误的观点呢？教师可以让学生从不同层面说明这一命题的错因。

生：我以为两个完全相同的三角形能拼成一个平行四边形，那么等底等高的三角形就是完全相同的。

生：等底等高的三角形面积是相等的，但形状不一定相同。

生：我们画过一些三角形的图，从中就能发现等底等高的三角形形状不完全是相同的。

生：平行四边形等底等高时，形状也不相同，不同图形分割成的三角形也不相同。

师：刚才几位同学都非常好，把各自的观点进行了讲解，而且用不同的方法使问题更明白，现在你们知道这道判断题的对错与否了吗？从这道题你还想起了哪些有关的知识呢？

……

课堂上要让每个学生都愿意把自己的观点亮出来，哪怕是错误的，大家也能从中得到有益的收获。无论是正面的阐述，还是据理力争，在彼此思维的碰撞后，能澄清固化的观念，对数学问题的理解变得透彻和清明。

三、顺势而为，于拓展延伸间融通

对于习题的设置，也需要从不同的视角来切入。数学的教与学不能一味地被动，顺向思考，促其生成；反其道而行，助其生长。比如面积教学中，先让学生“因式寻图”，运用“（5+3）× 3÷2”这个梯形面积计算的算式，计算下列由两个正方形组成的图形中的阴影面积。

接着，再深入进行“循式画图”，要求学生连接正方形的某几个顶点，构成一个图形，涂上阴影，求阴影部分的面积。把知识反哺深化，让学生借鉴刚才的图形研究，自主编题构成系列的求阴影部分的面积。

这样的设计，使练习不流于表面，不滞留在被动完成任务这一层面。通过设计图形这一开放式的题型，举一反三，将曾经学到、感知过的数学知识点一一唤醒，不断反刍，应用于当下。知其所以，还能知其所以然，把形与式进行有效沟通，融通知识间的关系，使学生对于数学的学习更为扎实而灵活。

数学教学离不开习题的设计，特别是面对不同的学生，适合的问题，适切的引申，适度的拓展，顺应学生的思维，才能相得益彰。同时，练习也不单纯是教师单方面的一种给予，基于学情，因势利导，用习题激起学生学习的起点，激活经验的热点，厘清知识间的盲点，解决问题的疑点，才能让学习深度发生，互动生成，让课堂更显精彩。