唱情歌前的调音?三角函数公式也许能帮你!
溦之洸茫(译)
有些时候,那些仅从理论角度看上去有意思的数学公式可以揭示与某些应用问题的意想不到的联系.
以三角学中“和差化积”公式为例
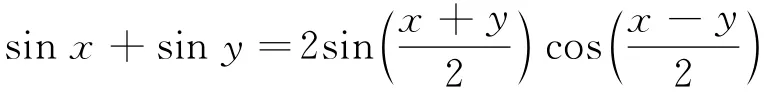
这个公式在解释“差拍”这个声学现象时会有直接的应用,让我们看看这到底是怎么一回事.

图1
差拍
当你同时弹奏两个频率很接近的音时,合成出来的音听上去时有时无,好像某人在以一个固定的频率调大和调小音量,这种现象就叫做差拍.三角函数公式会帮助我们解释它.
f1(t)=sin(ω1t)
f2(t)=sin(ω2t)
弹奏的这两个音可以用具有频率ω1,ω2的两个三角函数表示(准确地说这两个是角频率,但简单起见,在这里就把它们称为频率).
作为一个非常好的近似,我们可以认为声学现象是线性的.如此一来,同时弹奏两个音符产生的声音就等于这两个单音的叠加.
S(t)=sin(ω1t)+sin(ω2t)
借助和差化积公式,我们可以将这个“声音”函数表示为

在最后的表达式中,我们定义了
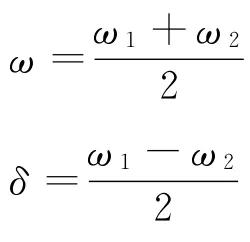
如果这两个频率ω1,ω2很接近,我们可以认为ω(ω1,ω2的平均值)和这两个频率也是很接近的.同时δ(ω1,ω2的差值的一半)在与ω相比时是一个非常小的量.
当δ远远小于ω时,我们可以认为它是一个对音符sin(ωt)的周期性放缩,放缩倍数为A(t)=2cos(δt).
S(t)=A(t)sin(ωt)
我们可以看出,A(t)扮演了一个周期性调节声音sin(ωt)的音量的角色.两个初始频率越接近,那么差拍频率δ就越慢(译者注:δ越小,周期就会越大).
在图2中,你可以看到一个例子,上图是两个函数f1和f2,下图是它们合成后的函数S.
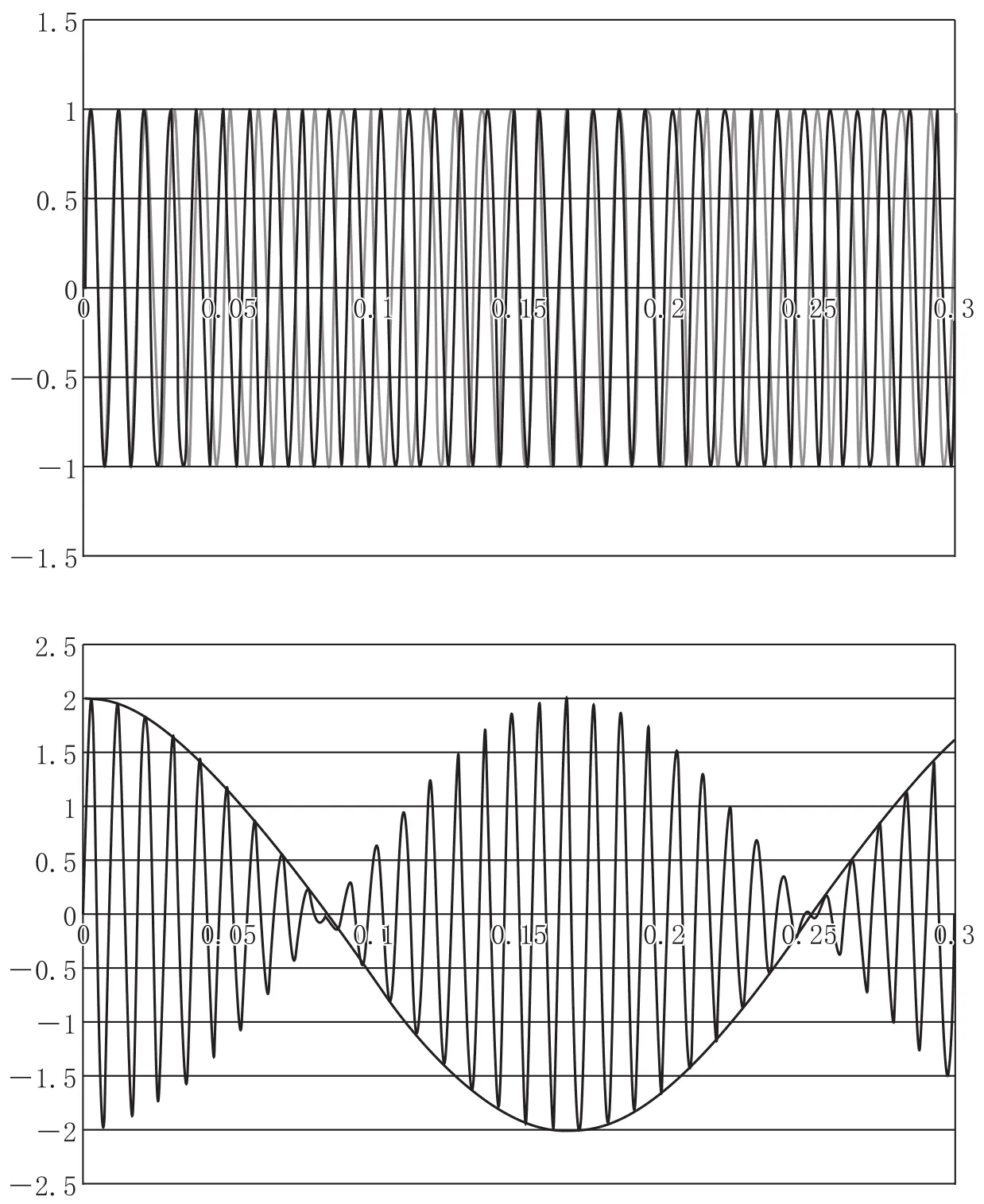
图2
乐器校音
差拍现象可以用于为乐器校音,让我们看看这是怎么进行的.
假设你现在需要借助一个音叉来为吉他校音,如果吉他的弦被调到与音叉的音相近的地方时,同时弹响它们就会产生差拍.通常地说,要通过提高或降低弦的张力来完美校音是很难的.通过反复试错则比较容易.
我们假设你试图提高弦的张力(也就是提高音的频率),你拨动了这根弦并敲击了音叉,于是听到差拍的频率增加了.这就说明提高弦的张力这法子是走反方向了.此时你应该慢慢减小弦的张力,直到差拍频率小到几乎不会引起注意.现在恭喜你,你的吉他弦与音叉产生的是同一个音(对于实际演奏而言,已经足够了).
剩下的5根弦呢,过程是一样的,只不过你借助的不再是音叉而是你所调好的那根弦的其他音.(译者注:吉他不同弦上可能会有同一个音,以调好的弦上的音为基准,找它在另一弦同样的音,进而校准这根弦)
当然,你可以借助电脑程序为乐器调音.但假设你现在在海滩或者路边上演奏吉他,周围是你的一群粉丝,而你正好没有电脑、手机没电.你最好知道怎么用传统的方法校准吉他,要不然你会瞬间掉粉的!

