灰需求下考虑缺货和中断风险的供应链网络设计

王海燕 王云瑜

(福州大学经济与管理学院, 福建福州 350108)

一、引言

经济全球化的发展使得供应链网络结构更具有复杂性。除了内部需求、汇率、成本等输入参数的不确定性，企业在运营时还面临着外部的干扰。一方面，越来越严重的环境问题导致自然灾害频发。据民政部2017年发布,我国受洪涝、干旱和地震等自然灾害的影响造成了3018.7亿元的经济损失。《每日邮报》消息称，2017年全球因为突发的环境灾害(主要是因为飓风“哈维”“伊玛尔”“玛利亚”的影响)造成的经济损失高达3060美元。另一方面，受人为因素影响，例如美味七七、博湃养车、爱狗团等由于管理不善导致资金链断裂，云南曲靖市青宇商贸有限公司卸焦油时因工人操作不当导致焦油泄露等，都给企业带来了巨大的损失。因此，如何设计出能够有效抵御风险的供应链网络迫在眉睫。谁能最有效地应对风险，对于消费者来说，无疑也是最值得信赖的。

根据Azad等的分类，供应链网络面临的风险分为内部参数的不确定和中断风险。参数不确定包括成本、需求、价格等参数的不确定。[1]Felix等考虑了零售商需求的不确定性，建立了一个多时期、多产品的三级供应链网络设计模型，使用非主导排序遗传算法(NSG-II)解决问题。[2]其他类似需求不确定的研究可参考赵广华等、李娜等的文章。[3][4]除了需求不确定外，还有诸如成本、价格等参数的不确定。Mari等考虑了产品需求、价格、回收率、建厂成本、运输成本、订购成本等参数的不确定性，使用隶属度函数将其转换成确定型模型后进行求解。[5]刘枚莲等将检测中心的处理能力、再制造中心的处理能力等因素设为模糊数，建立逆向物流规划模型，采用WinQSB软件进行求解。[6]其他类似研究可参考田俊峰等、赵霞等的成果。[7][8]而供应链中断则是由于外部原因，如自然灾害、经济危机等造成的风险。Ruiz-Torres等考虑在模型中加入多源供应和柔性生产两种方式来应对供应链网络中断的风险，采用决策树法考虑所有的可能状态。[9]Li等考虑供应端的供应能力无限制且易于发生中断，提出对供应设施进行投资设防，并为每个客户同时分配一个主供应商和一个备选供应商。[10]Jalali等假设分销中心容易受到中断风险的干扰，建立以最小化成本和最大化填充率为目标的混合整数规划模型。[11]其他类似研究可参考Torabi等、刘希龙等、卢梦飞等的成果。[12][13][14]

上述研究大都是使用已知其典型分布规律的随机规划或通过使用隶属度函数将不确定参数转化为确定性参数的模糊规划理论来处理不确定性，相对而言，面向灰色规划的研究还没有受到足够的重视。但是在现实生活中，灰色需求又是客观存在的。因此，考虑灰色需求下的SCN设计问题具有重要的意义。理论上，本文能够进一步扩充和完善不确定供应链网络的设计及优化问题；现实中，又能为处理灰色需求带来参考价值。因此，本文以客户点的灰色需求为特征，且允许客户点的缺货存在，考虑在中断情景下，以最小化供应链网络总成本为目标建立模型。

二、问题阐述及模型建立

(一)问题阐述及假设

相应的供应链网络结构如图1所示。

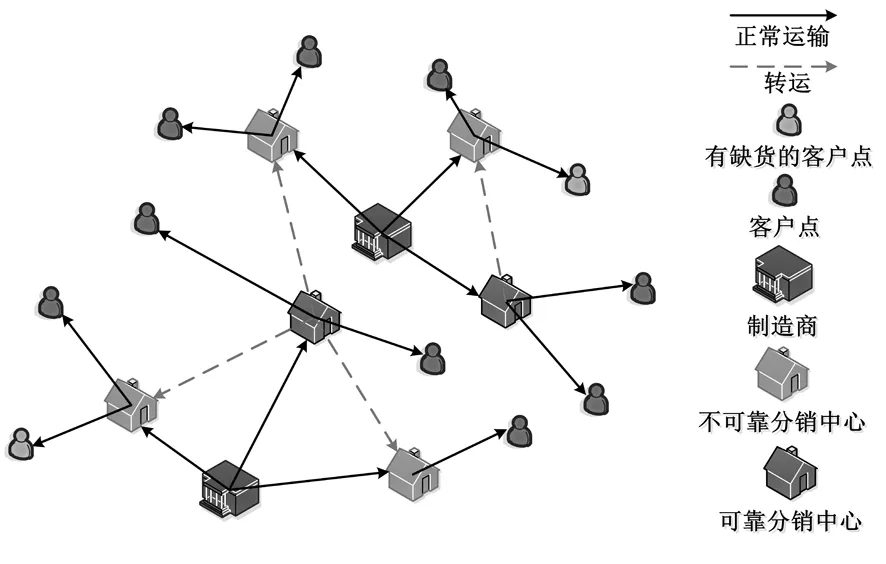
图1 供应链网络结构

制造商将生产的产品运输给分销中心。其中，备选分销中心的地理位置和储备能力已知，可分为可靠的分销中心和不可靠的分销中心两种类型，可靠的分销中心永远不会发生中断，而不可靠分销中心容易受人为因素(操作不当等)或自然因素(如洪水、地震等)的影响而发生中断，中断后丧失部分能力，该部分损失由可靠的分销中心补足。物流量运输到分销中心后便由分销中心运输给客户，不考虑分销中心的库存成本。在所研究的网络中，由于历史数据个数有限，只知道大概取值范围而无法模拟出确定的分布规律，此时假设客户点的需求为灰色是合理的。决策的内容包括应该选择建立哪种类型的分销中心，客户点的分配以及各个节点之间的物流量。

(二)符号及含义

(1)集合。I：制造商集合，i∈I；J：可靠分销中心集合，j∈J；M：不可靠分销中心集合，m∈M；L：所有分销中心集合，l∈L且L=(J∪M)；K：客户点集合，k∈K。

(2)参数定义。⊗dk：第k个客户的灰色需求量，du：灰色需求上限值，dl：灰色需求下限值；dab：从一个站点a到另外一个站点b的单位运输成本，a∈(I∪L),b∈(L∪K)；γl：分销中心l的配送能力,l∈L且L=(J∪M)；CRj：开放一个可靠分销中心j的固定成本；CUm：开放一个不可靠分销中心m的固定成本；qm：不可靠分销中心m的中断概率；pm：不可靠分销中心m中断后的能力损失比例；Max：一个很大的正数；Co：每单位缺货成本。

(3)决策变量。Uil：制造商i到分销中心l的物流量；FRjk,FUmk：分销中心j或m到客户点k的物流量；Tjm：中断后从可靠分销中心j到不可靠分销中心m的配送数量；YRj：可靠分销中心j开放为1，否则为0；YUm：不可靠分销中心m开放为1，否则为0；ARjk：客户点k分配给可靠分销中心j为1，否则为0；AUmk：客户点k分配给不可靠分销中心m为1，否则为0。

Ok:第k个客户的缺货数量。

(三)模型构建

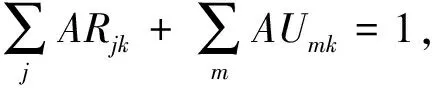
(2)

YRl+YUl≤1,∀l∈L

(3)

(4)

ARjk≤YRj,∀j∈JR,k∈K

(5)

AUmk≤YUm,∀m∈M,k∈K

(6)

Tjm≤Max·YRj,∀j∈J,m∈M

(7)

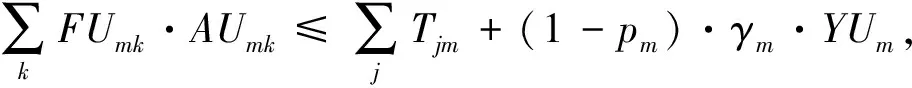
(8)

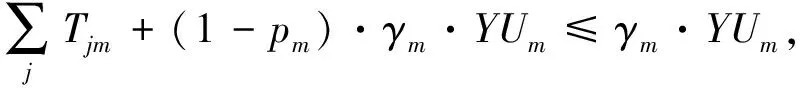
(9)

(10)

(11)

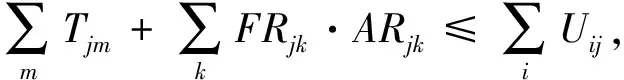
(12)

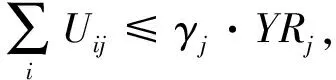
(13)

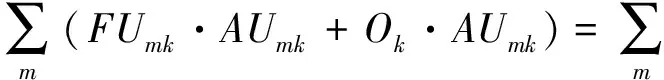
(14)

(15)

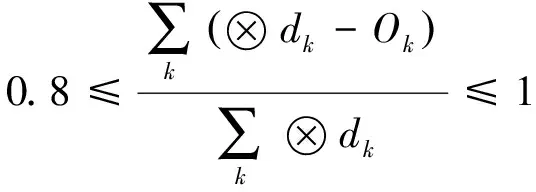
(16)

YRj,YUm,ARjk,AUmk∈{0,1};Uil,FRjk,FUmk,Tjm≥0

(17)

其中：式(1)表示SCN总成本的最小化；式(2)表示每个客户只能分配给一种类型的分销中心；式(3)表示在同个备选地点只能建立一种类型的分销中心；式(4)表示可靠的分销中心要建立一个或者一个以上；式(5)-(6)表示客户分配给开放的可靠/不可靠分销中心；式(7)表明转运量必须从开放的可靠分销中心流出；式(8)表示从不可靠分销中心流出的物流量要小于或者等于转运量和中断后能力剩余之和；式(9)表示对于不可靠分销中心而言，转运量和中断后能力剩余之和要小于或等于其配送能力；式(10)-(11)表示运输给客户点的物流量不超过制造商到分销中心的物流量与转运量之和，且不得超过不可靠分销中心的容量；式(12)-(13)为对制造商到可靠分销中心及可靠分销中心到客户点的物流量的约束条件；式(14)-(15)表示客户点的平衡约束；式(16)表示订单的满足率要在0.8和1之间；式(17)是对决策变量的约束。

(四)灰色参数处理

由于当前中断供应链管理实践还处于初步阶段，信息相对匮乏，因此本文采用等权均值方法来处理客户的灰色需求。

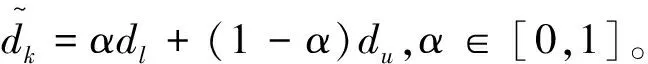
(18)

三、算例及分析

(一)算例结果及分析

以某公司为例，从5个备选分销中心中选择建立分销中心的种类及数量。该公司的供货商有2个，且为10个客户点提供服务。其中，部分参数如表1所示。

表1 随机生成的参数来源

各节点基本情况及相对位置图见图2。模型采用lingo软件求解，结果如表2所示。

图2 节点间的物流量

由算例结果可知：目标函数为1612726元，建厂成本为1354330元，其中开放的可靠分销中心编号为3、4、5，开放的不可靠的分销中心编号为1、2，运输成本为16306.48元，转运量为170，转运成本为225.24元，缺货量为51.88，缺货成本为241864.6元，订单的满足率高达96.9%，具体物流关系如图2所示。

(二)敏感性分析

为了更好地观察pm改变对中断供应链网络的影响，进行敏感性分析。调节pm的大小，观察中断情景下供应链网络各个成本及结构的变化，结果见表3。

表2 算例结果

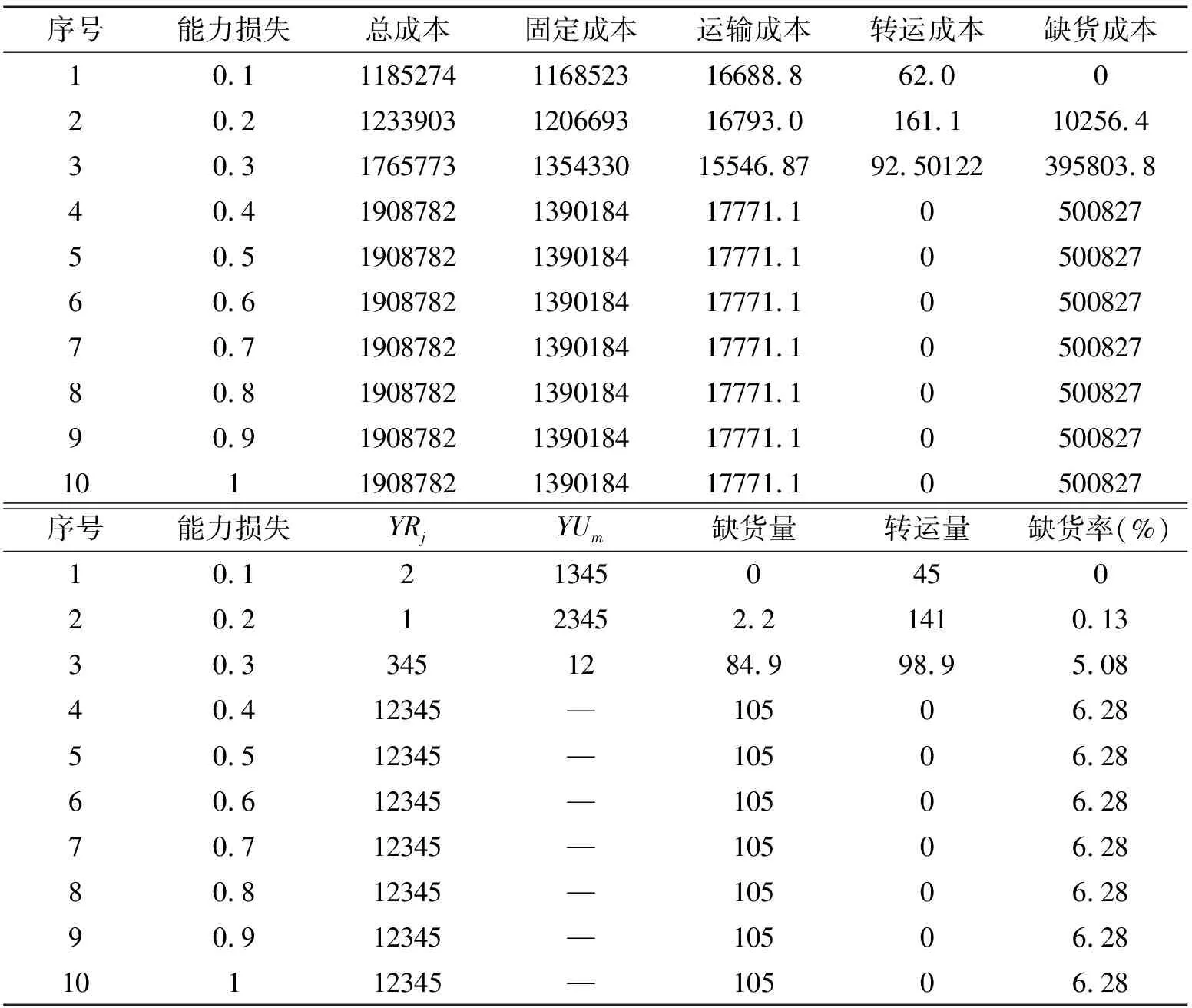
表3 敏感性分析(能力损失比例为0.1-1)

根据表3的结果，可知当能力损失比例越大，供应链网络的总成本呈现一个上升的趋势，且更倾向于选择开放可靠的分销中心。而当能力损失比例大于0.4之后，总成本等各个参数不再变动，原因是开放的分销中心都为可靠的分销中心，已满足所有条件，不再开放不可靠的分销中心，因此能力损失比例已不再干扰供应链的设计。

由表3可以看出，当能力损失比例大于0.4后，不可靠的分销中心便不再开放。因此，为了更详细地看出能力损失比例对供应链网络的影响，调节能力损失比例在0.1-0.42区间变动以便于比较结果。

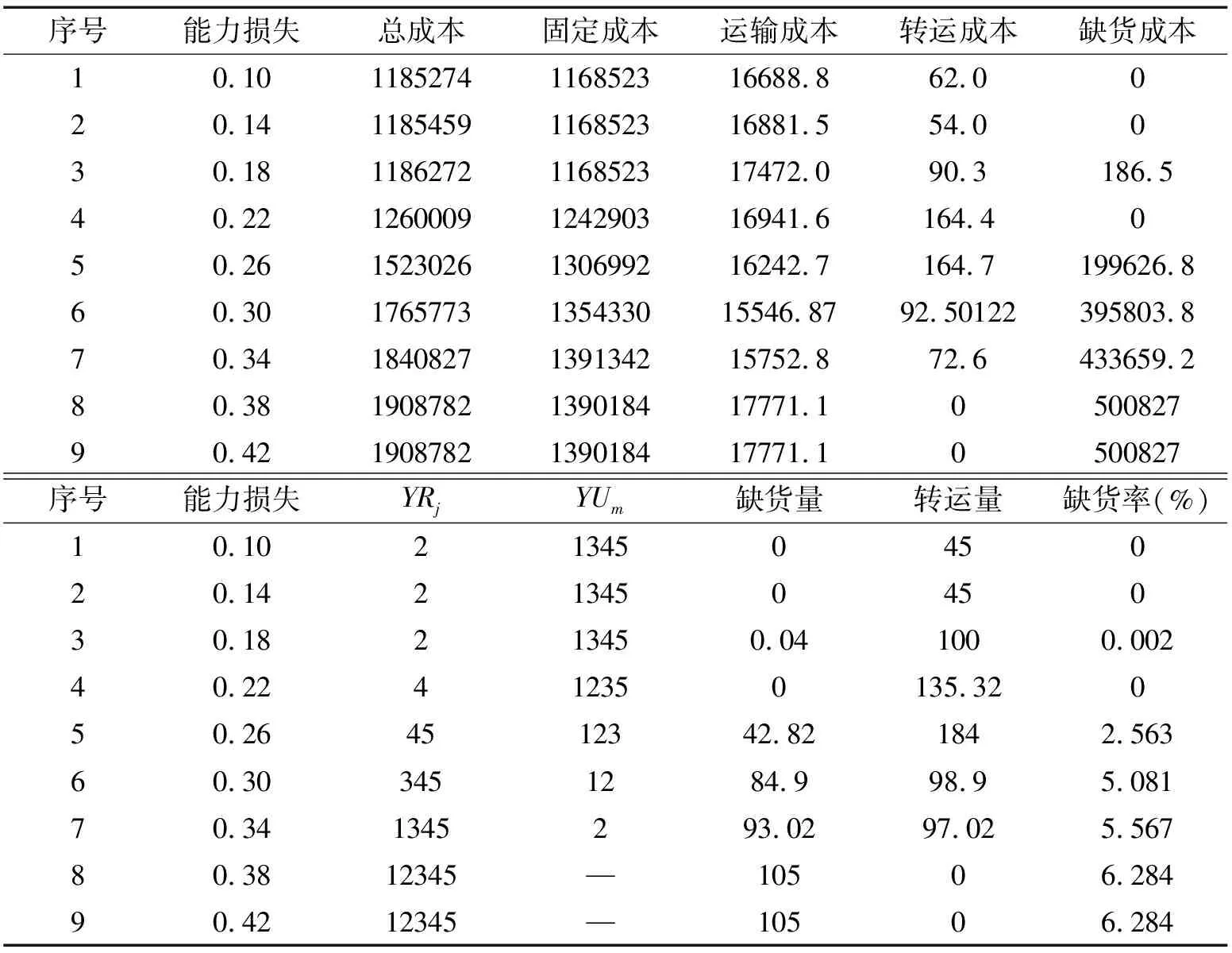
表4 敏感性分析(能力损失比例为0.1-0.42)

根据表4的结果，可知随着pm的上升，总成本呈现上升的趋势，而且对于分销中心的选择更倾向于选择造价高，容量大的分销中心。观察表4第(1-3)行可以发现，当选择开放的分销中心一样时，随着能力损失比例的增大，转运量和转运成本增加。观察第(2-4)行发现，开放一个造价更高、容量更大的分销中心的成本远比开放一个造价低、容量小的分销中心成本来得更高。因此，部分客户点会出现缺货现象，从降低整条供应链成本来说，这是可取的，但当企业为了做得更大更好时，也应将该情况纳入考虑，减少缺货现象，从而加强信任感，防止出现缺货而损失客户的情况。表4中的(3-8)行可以更直观地看出对分销中心的选择情况。

(三)与不考虑缺货成本的模型进行比较分析

本文将不考虑缺货成本的模型(假设为模型1)与考虑缺货成本的模型(假设为模型2)相比较，进一步说明增加该参数的必要性。模型1建立如下：

⊗dk·AUmk,∀k∈K

(20)

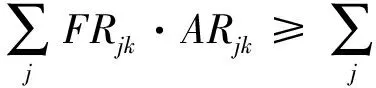
(21)

约束(2)-(13)和约束(17)-(18)

灰参数的处理以及模型的求解方式与模型2相同，对比结果见表5。

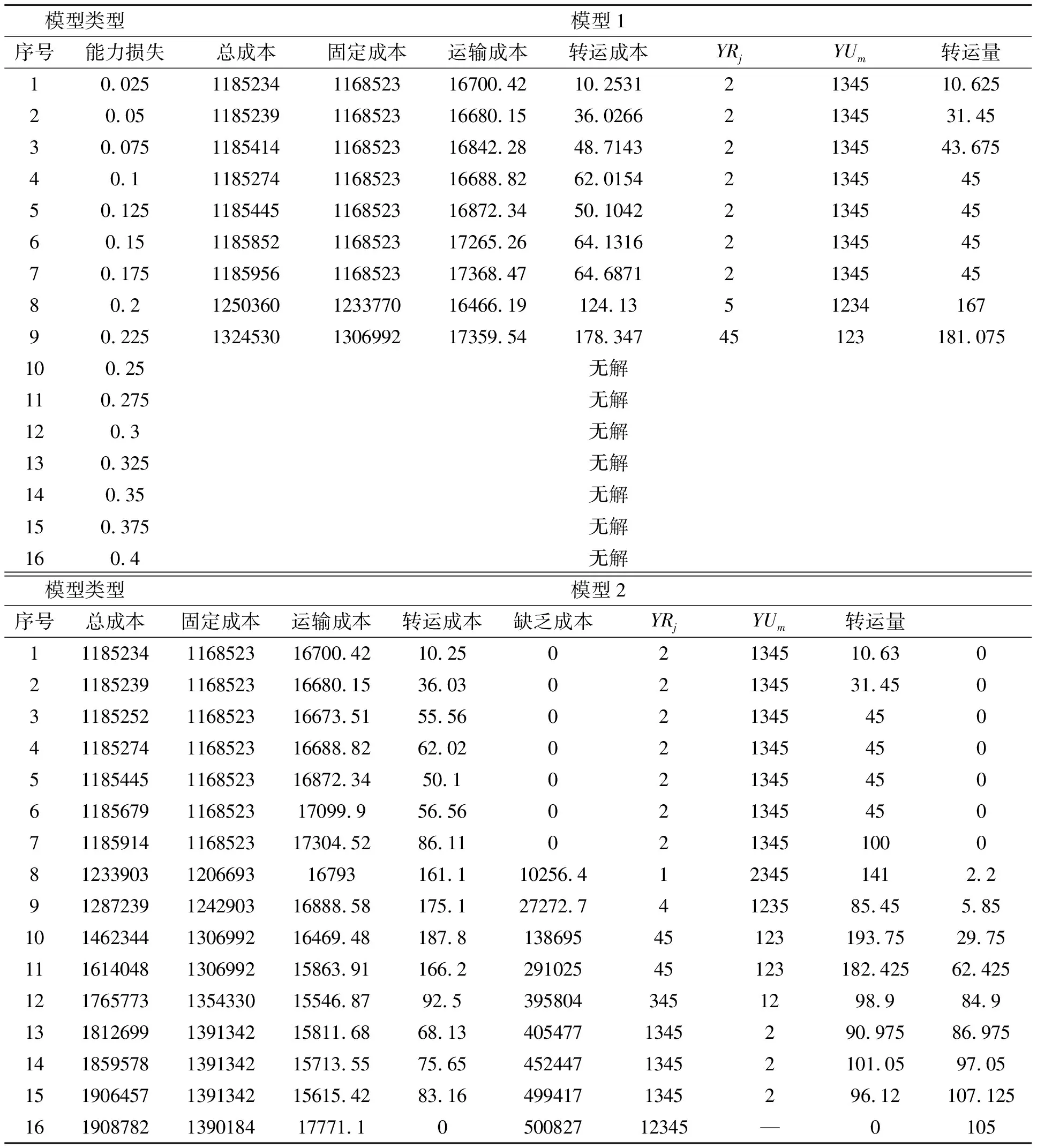
表5 模型1与模型2对比结果

由表5结果可得：当能力损失达到0.25及以上的时候，模型1无解，而模型2依然能够进行计算，说明模型2更具有实用性和广泛性。比较第1行到第9行，当能力损失比例为0.025、0.05、0.1、0.125时，模型1的总成本与模型2的总成本相等，且各个成本、分销中心的选择等都是一致的，而当能力损失比例为0.075、0.15、0.175、0.2、0.225时，模型2的总成本比模型1更小，对比第8行和第9行，模型2选择了特别少量的缺货来降低总成本。因此，从整体来说，考虑缺货成本比不考虑缺货成本的决策在总成本目标上具有更大的优势，也更能够增强实际决策的灵活性。

四、总结及展望

中断供应链网络设计问题是供应链网络研究的重点之一。本文针对这一问题，在中断情景下，结合客户点的灰色需求为特征建立模型，采用等权均值白化方法进行求解。对于易受干扰的不可靠分销中心采用转运策略降低风险因素的影响。求解结果表明：

(1)当能力损失比例越大，供应链网络系统的总成本呈现上升趋势，且更倾向于选择可靠的分销中心；

(2)当选择开放的分销中心一样时，随着能力损失比例的增大(pm≤0.4)，转运量和转运成本增加；

(3)若开放一个造价更高、容量更大的分销中心的成本远比开放一个造价低、容量小的分销中心成本来的更高的时候，以供应链总成本最低为目标的企业宁愿选择让部分客户点出现缺货现象也不会选择开放一个更可靠的分销中心；

(4)在供应链网络设计中，允许一定的缺货成本存在，在一些情况下，更有助于降低系统总成本，增强决策的灵活性。

接下来的研究可进一步丰富对于模型中灰色变量的处理方法，如结合机会约束规划理论，将灰色规划模型转化为灰色机会约束模型，使用智能算法进行求解。除此之外，也可考虑使用情景法模拟不同情景，或者采用其他风险缓解策略(如投资设防策略或者期权策略等)来降低供应链网络总成本。

注释：

[1] Azad N., Davoudpour H., Saharidis G. K. D., et al.,“A new model to mitigating random disruption risks of facility and transportation in supply chain network design”,InternationalJournalofAdvancedManufacturingTechnology, vol.70,no.9-12(2014), pp.1757-1774.

[2] Chan F.T. S., Jha A., Tiwari M. K.,Bi-objectiveoptimizationofthreeechelonsupplychaininvolvingtruckselectionandloadingusingNSGA-IIwithheuristicsalgorithm, Elsevier Science Publishers B. V.， 2016.

[3] 赵广华、刘佳怡：《需求不确定条件下生鲜农产品供应链网络设计》，《物流技术》2017年第10期。

[4] 李娜：《不确定需求和配送时间窗约束下的供应链优化》，《计算机仿真》2015年第4期。

[5] Mari S. I., Lee Y. H., Memon M. S.,“Sustainable and Resilient Garment Supply Chain Network Design with Fuzzy Multi-Objectives under Uncertainty”,Sustainability, vol.8,no.10(2016),p.1038.

[6] 刘枚莲、李丹、邱建伟：《带有模糊参数的电子废弃物逆向物流规划模型》，《交通运输工程学报》2011年第3期。

[7] 田俊峰、杨梅、岳劲峰：《具有遗憾值约束的鲁棒供应链网络设计模型研究》，《管理工程学报》2012年第1期。

[8] 赵霞、曹宝明、窦建平：《需求和原料价格不确定下农产品供应链网络鲁棒优化设计》，《管理工程学报》2017年第4期。

[9] Ruiz-Torres A. J., Mahmoodi F., Zeng A. Z.,Supplierselectionmodelwithcontingencyplanningforsupplierfailures,Pergamon Press, 2013.

[10] Li Q., Zeng B., Savachkin A.,Reliablefacilitylocationdesignunderdisruptions,Elsevier Science Ltd， 2013.

[11] Jalali S., Seifbarghy M., Sadeghi J., et al.,“Optimizing a bi-objective reliable facility location problem with adapted stochastic measures using tuned-parameter multi-objective algorithms”,Knowledge-BasedSystems, vol.95 (2016),pp.45-57.

[12] Torabi S.A., Baghersad M., Mansouri S.A., “Resilient supplier selection and order allocation under operational and disruption risks”,TransportationResearchPartELogistics&TransportationReview, vol.79(2015),pp.22-48.

[13] 刘希龙、季建华：《基于多源供应的弹性供应网络研究》，《工业工程与管理》2007年第3期。

[14] 卢梦飞、陈伟炯、梁承姬：《缓解中断风险的应急供应链网络鲁棒优化》，《合肥工业大学学报》(自然科学版)2015年第10期。